A study on the effect of thermal changes on the fall and subsequent rise of a synthetic rubber sphere!
Table of Contents
Everyday we use essential materials without paying attention to their physical properties, assuming that their properties will be constant and their functions reliable. Although it is not always necessary to completely comprehend the scientific mechanics of particular materials, it is often wise to understand the meaning of the materials’ physical properties. The material to be dealt with in this experiment is one that is found in about 50,000 products, rubber (World Book 1977). Rubber, although it may appear to be a simple, permanent material to us, is susceptible to change in varying conditions as any other form of matter is. We know that rubber is elastic and “not stable to temperature changes” (Hawley 1981), therefore, synthetic rubber will be a good material to experiment with as it is similar to rubber in performance.
In our casual use of domestic or industrial
materials, such as rubber, we are likely to forget that the materials we are
working with are only helpful or accurate under certain conditions.
One condition, temperature, is perhaps the most significant factor when
dealing with varying conditions. Not
only does temperature, which can be controlled by the addition of heat to a
system or substance, define the qualitative “sensation of warmth or
coldness” of a material but the amount of kinetic energy within the molecules
of the material (Lynds 1995). According
to thermodynamic theory, adding heat to a substance will increase the overall
energy within the substance by a factor directly related to the increase in heat
(Weast 1974). Adding heat to a
material can also effect the state of the material, but, in this experiment,
state changes will not be discussed. Instead,
the experiment deals with the physical performance of a common material,
synthetic rubber, when it is exposed to varying amounts of heat.
Specifically, the problem at hand deals with the effect that varying temperature changes will have on the elastic properties of synthetic rubber. A commonly found synthetic rubber sphere, known as a bouncy ball, will be used as the object that will be manipulated and measured. A bouncy ball bounces because of the elastic springiness that quickly returns the ball to its original shape after it has been deformed (World Book 1977). Will the ball be more elastic in higher temperatures or in lower temperatures? In order to measure the elasticity of the rubber ball, it will be dropped and its rebound height will be recorded. In a similar experiment with synthetic rubber by Sorlien, bouncy balls were found to bounce higher under higher temperatures, and the result was attributed to the increased flexibility of the cross-linking of the molecules themselves (Sorlien 2000). Taking into account the information presented, specifically Sorlien’s experiment and the evidence that heat will effect the elasticity of natural of synthetic rubber, we hypothesize that the synthetic rubber sphere will bounce higher when its temperature is higher.
The process of measuring the height of the bouncy ball once it has been heated or cooled to a desirable temperature is rather simple. We repeatedly dropped the same synthetic rubber ball from a height of one meter while changing the temperature of the ball between drops. The materials for the dropping aspect of the experiment, where we collected data, are as follows: a bouncy ball constructed of synthetic rubber, a piece of construction paper labeled vertically in centimeters from the ground to one meter (taped to a wall), and a video camera to record the bounces. The ball was always dropped on the same area of concrete in a garage. Once the ball had been exposed to a consistent temperature for 20 minutes (the fact that we left the ball in for 20 minutes each time is important – any inconsistency in time of exposure would cause our results to be less valid), the ball was transported as quickly as possible to be dropped in order to minimize the loss or gain of thermal energy put on the ball and the surrounding environment. While one person positioned the video camera such that the picture portrayed an accurate view of the area in which the ball was dropped from and tends to bounce back up to, the other person positioned the ball so that the lowest point on the ball was one meter from the ground (with the help of the labeled construction paper and the directions of the camera operator). Once the ball was level with one meter, it was let go and allowed to rebound. Since our experiment is only designed to measure the initial rebound height of the ball, the video camera was shut off after the first rebound. In order to analyze our data, we replayed the video (with a computer program; freezing the frame at the ball’s highest point) and noted the highest elevation that the ball reached on its rebound.
The difficult part or our experiment was attempting
to heat or cool the ball to certain temperatures. Originally, our plan was to manipulate the temperature of the
ball such that we could have 21 data points ranging from 0°C to 100°C,
but we soon found it very difficult to manipulate the independent variable
(temperature) steadily, especially in increments of 5°C. We attempted to place the ball in hot and cold water, but we
were unable to find a way to keep the temperature of water (unless it is
boiling, at room temperature, or mixed with ice) steady for 20 minutes.
We also had trouble getting the ball to the drop site quick enough,
because it cooled down significantly as we dried it off.
Finally, this method did not work because the bouncy ball floats and was
not entirely exposed to the water.
Eventually, we determined that prolonged exposure to a variety of temperatures had to be done through the use of an oven, space heater, refrigerator, freezer, plastic bag placed in ice water, and the differing temperatures of the environments in and outside of a house. All of these methods require the manipulation of the air temperature around the ball in order to heat or cool the ball itself. A thermometer with a sensory extension was used to measure temperatures in the environments we exposed the ball to. Without a device that could accurately manipulate the temperature in consistent increments, we were forced to do the best we could by obtaining data points that have a variety of deviations between them. For instance, we were unable to obtain a temperature between -18°C and 1°C, but we were able to make a data point at 6°C. In reality, this does not cause much inconsistency in our results, but it does make our line of best fit slightly less accurate. Below is a list of all the methods we used to heat up and cool down the ball:
Ice box of freezer: Ball left in ice compartment of freezer: -18°C
Plastic bag: Ball placed in bag that was placed in ice water (allowing the ball to remain dry): 1°C
Refrigerator: Ball put in refrigerator: 6°C
Garage: Air temperature in garage: 15°C
Kitchen: Air temperature in kitchen: 21°C (used as “room” temperature for purpose of experiment)
Space heater: Ball placed at 2 different distances in order to vary temperature: 32°C and 45°C
Oven: Used for all remaining temperatures – slightly cracked open for 55°C – closed and controlled through the oven’s temperature dial for 65°C, 70°C, 80°c, 90°C, 100°C, 140°C
The ball was dropped 14 different times after being exposed to different temperatures. The following data table shows how high the ball rebounded under different temperature after being dropped from one meter. Two significant figures are used when recording heights, because we were unable to get more accurate with the video equipment that we were using.
|
Drop Number |
Temperature in Celsius |
Height of Bounce (cm) |
||
|
1 |
-18 |
78 |
||
|
2 |
1 |
83 |
||
|
3 |
6 |
83 |
||
|
4 |
5 |
83 |
|
|
|
6 |
32 |
87 |
||
|
7 |
45 |
86 |
||
|
8 |
55 |
89 |
||
|
9 |
65 |
86 |
||
|
10 |
70 |
89 |
||
|
11 |
80 |
90 |
||
|
12 |
90 |
91 |
||
|
13 |
100 |
92 |
||
|
14 |
140 |
92 |
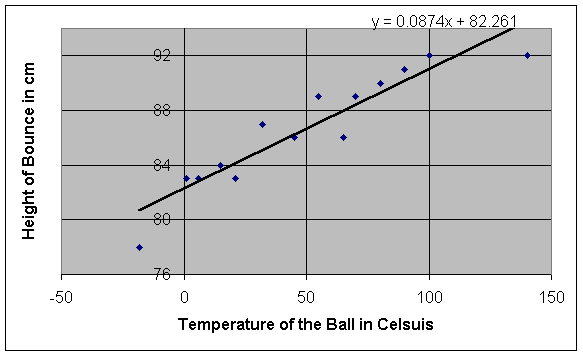
It seems that the height of the bounce eventually increases as the
temperature of the ball rises. In
order to demonstrate the difference in height between the two extreme
temperatures in our data table (-18°C and 140°C),
we dropped two balls simultaneously and recorded the results on video (we
actually had five balls of the same make, but we used only one to remain
consistent throughout the experiment). As
we expected, the 140°C ball bounced much higher than the -18°C ball did (92 cm high as opposed to 78 cm
high – a difference of 14 cm). While
this method of experimentation seems to easily prove our hypothesis, we must
look at a series of data points, like the ones we have taken, before coming to
any conclusions.
We must ask two questions: what kind of relationship
exists between temperature and height, and what is the uncertainty of our
results? To answer the first
question, we must analyze the graph of our data (see page 7). At first sight, the relationship between temperature and
height of the bounce appears to be linear.
Of course, we can’t be absolutely sure that this relationship is
linear, especially with uncertainty taken into consideration, but we can attempt
to find a linear relationship by finding a line of best fit for the data.
Entering the data into a graphing calculator and calculating a line of
linear regression leaves us with the following equation for our line of best
fit:
y = ax + b, where a = .0874 and b = 82.2609, therefore, y = .0874x + 82.2609

Without
taking uncertainty into account, we can assume that this equation represents a
general equation for the relationship between the temperature of a ball and the
height of its bounce when dropped from one meter.
Visually, this line of best fit appears to match the general trend of the
data well. The slope, represented
by a in the general equation, is equal
to .0874, therefore, the height of the bounce should increase by .0874 cm when
the temperature increases by 1°C. The fact that the insertion of various values for temperature
into the equation for the line produces results similar to those that we
obtained experimentally shows that the
relationship is indeed linear.
We need to look at the impact uncertainty has on our line of best fit. In order to measure the uncertainty our results, we dropped the bouncy ball five times when its temperature was 21°C. The table below shows the results of these five drops:
|
Trial Number |
Height in cm |
|
|
1 |
84 | |
|
2 |
||
|
3 |
82 |
|
|
4 |
83 |
|
|
5 |
85 |
Taking the
average of these five heights gives us 83 cm, which is the also the midpoint of
the five values. If the ball can
vary from its mean height at a certain temperature by 2 cm, then we must assume
that our uncertainty is 2 cm, and
each data point could be +/-2 from what we found it to be. We have applied this uncertainty not to our individual data
points but to our line of best fit to see if our uncertainty will affect the
kind of linear relationship that we believe to be present between temperature
and height. The graph on the page
seven shows the effects of a 2 cm uncertainty on our line of best fit.
Although the slope of the line is altered with uncertainty, the
relationship between temperature and height remains direct and linear.
We can conclude the following from our results: if the temperature of a
synthetic rubber bouncy ball is increased, then it will bounce higher when
dropped from a height of one meter. Similarly,
if the temperature of a synthetic rubber bouncy ball is lowered, then it will
bounce lower when dropped from a height of one meter.
Although we were
able to prove our hypothesis correct, there are some improvements to our
experiment that could be made in order to obtain a more accurate sense of the
relationship between the temperature and height of the ball. First of all, our results would have been more accurate had
we recorded the ball dropping at each temperature a number of times, rather than
just recording several drops from 21°C
to obtain a value for uncertainty. It
is possible that the uncertainty may not be 2 at different temperatures,
therefore, the uncertainty on our line of best fit is approximate.
Of course, our line of best fit is also approximate, because we were
unable to heat the ball so that we could have a consistent interval between
temperatures. A second improvement
that could be made to our experiment is our method of transporting the ball to
the drop site. Unfortunately, the
ball lost or gained thermal energy as soon as it was removed from its extreme
environment and exposed to room temperature, and its temperature was slightly
altered by the time we dropped it. To
measure the ball’s true temperature at the time of the drop, we should have
used Newton’s Law of Cooling (Temp = T +
Ae^(kt), where T is the temperature of
the outside environment, A and k are constants, and t is time) and recorded
the time that the ball was exposed to room temperature before it was dropped.
Although our technique for measuring the height of the ball’s bounce
was more accurate than using the naked eye, we were still only able to
approximate the ball’s height. With
a higher quality video camera, we would have been able to measure the height of
the ball to the nearest millimeter. Also,
the ball was not always dropped from exactly one meter, due to human error.
A more efficient system for dropping the ball would have minimized the
amount of variables that were present in addition to the independent variable.
Finally, the ball itself is not completely round due to the quality of
its manufacturing.
Despite the numerous possibilities for improvement found in this
experiment, we have still managed to prove our hypothesis correct.
We must now ask the following: why does the ball bounce higher when it is
heated and lower when it is cooled? There
are two main scientific concepts that cause the ball to bounce higher when it is
heated; the first is the idea that heat affects elasticity, and the second is
the concept of heat as energy. First
of all, the ball increases in size when it is heated.
The change in the ball’s volume after being heated is equal to the
product of synthetic rubber’s coefficient of volume expansion, the ball’s
initial volume, and the change in temperature (uV = BVouT).
In order to be sure that the bouncy ball does indeed expand when heated,
we measured its volume at two different temperatures by measuring its
displacement in water. When the ball was at 21°C
(room temperature) and placed in 4 oz of water, the water level went up by .4
ounce. When the ball was at 140°C, the ball caused the water level to rise .5
ounces ounces, thus the volume of the ball increased by approximately .1 ounces.
Of course, this method is not very accurate for measuring the degree by
which the volume increases, because the ball cools as soon as it is placed in
the water, but it does show that the ball’s volume does indeed increase by
some factor. In fact, we could see the water level drop as the temperature
of the ball decreased (only with the aid of marks on the container).
Despite this change in volume, the ball’s mass remains constant,
therefore, the ball is stretched out when it is heated up.
This stretching gives the ball more snap when it rebounds off the
concrete surface. On a microscopic scale, the molecules of the ball themselves
are allowed to move more freely when heated, therefore, the ball experiences a
slight loss in rigidity and is made more flexible.
In terms of energy, we know that adding heat to a substance will raise
the kinetic energy of the molecules within that substance, and the same is true
for our synthetic rubber bouncy ball. Owing
to the fact that heat added to a system directly increases the energy of that
system (for example: Q
= mcT),
we know that the ball’s total energy is increased when its temperature is
increased. It is possible that this
increase in energy is what causes the ball to bounce higher, but that is a whole
different experiment altogether. Just
to see if the kinetic energy of the ball is increased by heat, we calculated the
kinetic energy of the ball at two different temperatures. The ball was
dropped three times at each temperature. The height at 21° was assumed to
average 83 cm, and the height at 140° was assumed to average 92 cm (these
values are based on the results we obtained in our experiment and verified by
the naked eye during these drops - not very accurate, but we are looking for a
conceptual relationship here). The ball was timed from the time it left
one meter, bounced, and returned to the ground, therefore, the ball traveled a
distance equal
KE = .5mv²
At 21°C, the mean t = 1.19, therefore, v = (.83 + .83 + 1)/1.19 = 2.24 m/s
.5mv² = .5m(2.24)² = 2.51 Joules
At 140°, the mean t = 1.19 also, but the height is different. v = (.92 + .92 + 1) = 2.84 m/s
.5mv² = .5m(2.84)² = 4.03 Joules
What we have just done in attempts to briefly measure the effects of heat on the volume and kinetic energy of the ball should really be done in separate experiments with multiple trials and measurements of uncertainty. There are many other directions that can be taken with the information that we have amassed in this experiment. For instance, it would be interesting to study the second, third, or even tenth bounce of the ball, rather than just the first. Even with the single conclusion we have made in our experiment, our finding are still important in the real world. We have learned that changing the temperature of a synthetic rubber will alter at least its elastic performance, and perhaps even its volume and the kinetic energy of its molecules.
Links - Here lie some links to help you expand your knowledge of this incredibly interesting topic. Warning: user accesses links at his/her own risk!
-"Government Rubber" and "United States Synthetic Rubber Program"- If you want to know about the history of synthetic rubber in the United States, these sites are for you. http://www.psrc.usm.edu/macrog/exp/rubber/synth/asrrp.htm and http://www.acs.org/landmarks/rubber/rbb_war.html It turns out that the U.S., our beloved homeland, began producing synthetic rubber during World War II. Maybe I should thank Hitler for making this experiment possible . . .
-"School of Polymers and High Performance Materials" - All you ever wanted to know about polymers can be found on this page, http://www.psrc.usm.edu. To observe an experiment very closely related to mine through video download, follow the links to http://www.psrc.usm.edu/macrog/demos/bball.htm. The site was provided by the University of Southern Mississippi.
-"Bouncy Ball" - Play around with a bouncy ball by manipulating things other than temperature on the cool, interactive site. http://wso.williams.edu:8000/~dbennett/BallControllerLab.htm http://tuhsphysics.ttsd.k12.or.us/Physics/Research/ib00/MattWeb/Webpage.htm
Bibliography
Hawley, G. Gessner. The Condensed Chemical Dictionary. ©1981, Van Nostrand Reinhold Company, New York, New York. Pp. 902
Background Information Procedure Results Discussion Links Bibliography Table O' Contents