The Mapping of Sound Waves as Emitted by Two Simultaneous Sound Sources in the Tualatin High School Auditorium, and the Resulting Acoustical Phenomenon

Dave Shelley

Research Project

Tualatin High School

Abstract

Works Cited

Links

Return to research

Abstract

The research question being investigated is whether or not the designers of the Tualatin High School auditorium achieved the goal of having little to no dead spots present, while having an equally distributed sound pattern.The scope of this investigation is fairly narrow.I have chosen to take data from the first half of the auditorium, and analyze it in the form of decibel vs. difference in wavelength graphs and intensity vs. distance graphs.I have come to the conclusion that the engineers did a good job designing the auditorium.There were no dead spots in the seating area, and there was an equally distributed sound pattern throughout.

Table of Contents

Introduction

Background Information

According to Vern Knudsen, “Acoustics is one of the oldest branches of physics,” (Knudsen 1963).Incorporating acoustics into auditoriums started about 2,500 years ago with the work of Pythagoras (Knudson 1963).The Greeks and Romans used early acoustical techniques in their theaters and arenas.Since then, the design techniques have changed dramatically, although the same goal is always in mind: to have a balanced sound everywhere, and to minimize the dead spots and focal points.The Tualatin High School auditorium, costing several million dollars, is supposedly on the cutting edge of today’s acoustical designs.

Statement of Problem

The purpose of this investigation is to map out the sound patterns in the High School auditorium, and to see how well the engineers have accomplished their goal.I will attempt to locate the dead spots, or destructive interference, as well as the points of constructive interference and any focal points.

Review of Related Literature

According to George Trigg, sound impulses emitted by multiple sources arriving at a listener is a composite of the direct sounds and reflections from the walls, floor, and ceiling of the room (Trigg 1997).This means that there are a lot of factors that go into the sounds at certain points in a room.There are a few simple but important equations I will use in this research.One is l= v/f (Giancoli), where l equals the wavelength in meters, v equals the velocity in meters per second, and f equals the frequency in Hz (Giancoli 1991).Another useful tool for this research is the idea of constructive and destructive interference.In order to measure the interference we first must measure the wavelength.If the interference is destructive, then the difference between number of wavelengths from the speakers to the chosen point is .5, 1.5, 2.5, etc. (Berg 1995).It is the opposite for constructive interference; the difference between the number of wavelengths is close to a whole number, 1,2,3, etc. (Berg 1995).According to Knudsen, it is the job of the engineers to consider all of these factors when building an auditorium (Knudsen 1963).Their goal is to make sure the constructive interference is not high, and to lower the number of dead spots using wall and ceiling shapes for echoes.

Statement of Hypothesis

It seems relevant to see how well the engineers of the auditorium did their job.I hypothesize that there will be almost no dead spots, and likewise, almost no focal points of sound in the new auditorium.

Table of Contents

The Method

It’s two weeks before the due date, and like everyone else, I verbally abuse myself for not starting earlier.Here I am in the high school auditorium at 7:30 pm doing physics, when I could be at home watching the Simpsons.Heck, if I take too long, I could even miss the A-Team.Coming to this realization, my mood dropped and I thought of quitting IB for good.A little scale appeared in my head; on one side, IB, and on the other, the Simpsons and A-Team.Then I thought of all the benefits of IB: money, women, and fame.I must carry on.Even though the results of my project will not be earth shattering, they could benefit the future performers in the auditorium.Oh yes, I must carry on.

In order to successfully complete the experiment, I had to think of a way to take steady sound readings from different seats in the auditorium, procure the supplies to do this, and hardest of all, find the time to do this.I will start with the design of my procedure.

I started with a stereo that had two speakers.Attached to the stereo was a microphone, and next to the microphone was an electric tuner set to 220 Hz. I also needed an extension cord because my stereo’s plug couldn’t reach the wall socket.To take the data, I used a sound meter and a long tape measure.Here is a diagram of the set up for the equipment:

The microphone would pick up the tuner’s pitch, and the stereo would produce and amplify that pitch into the auditorium.This all works on paper, but when I actually tried to set it up, for some reason, the speakers let out high-pitched squeaks.I looked up this phenomenon in one of my physics sources, and discovered that my problem was with feedback.I determined the problem was with the microphone’s chord; it was too short.This made it too close to the speakers, and the microphone picked up the tuner and the speaker’s noise, thus the squeak.I had two options in solving this problem; one, I could go to a friend and beg for the use of their long corded microphone, or two, I could quit IB.I chose the first path.My friend said yes, and I hoped that all the impediments I would run up against could be solved this easily. Now that I know what equipment I will need, the next step is how to obtain it.

Like I mentioned earlier, I borrowed the microphone from a friend, and I already owned the stereo, tuner and extension cord.That leaves the sound meter and the tape measure.For the tape measure, I decided to check one out from my teacher.I checked out a 30 meter one, and it turned out to be of sufficient length.The sound meter was the next huge problem; our teacher only had one, and there were about four other people needing to use it.Because everyone waited until a few weeks before the deadline, there was a mad dash for the sound meter.I lost.I had to plead with the winner for use of it on the nights I took data.He let me, so I was set.I had everything I needed and only had to figure out a time I could use the auditorium.

Scheduling auditorium time was another tricky maneuver.I couldn’t do it during school because there was class, and I couldn’t do it after school due to play rehearsals.My only option was to do it at night, and finally I hit a bit of luck; the basketball season had just started, so my band director was already at school for the pep band.The games lasted from 7:30 to 9:00 and it took me four sessions in the auditorium to finish.My director would let me in the auditorium at 7:00, and I would leave when the basketball game was over.You can imagine the pain I felt when I realized IB was depriving me of the chance to play pep band at the games.Oh well…life goes on.

My first night in the auditorium was taken up entirely with measurements.I set up the equipment, and measured where it was on the stage.I came up with a diagram that looked like this:

After that, I began measuring the distance between the speakers and the seats.I went in thinking I would do all the seats in the auditorium.Then I realized that with only one person working, that would take years, so I decided to take fewer data points. I decided to use only the first half of the auditorium (six rows) and only take data on every odd chair number.This somewhat decreased my workload, but still left a modest amount for me to do.The rest of the first night, all of the second night and part of the third night consisted of finding the distance between the speakers and the seats.To do this, I taped the end of the tape measure on the stage at speaker A.I then went to the seats and found out the distance from that speaker.This was a grueling task; I had to hold the tape measure, the data pad, and write the measurements on the pad.These are three easy tasks, but one person working alone only has two hands to use.I spent the time juggling my equipment while taking data.Also to add to my frustration, the tape measure kept detaching; at about the middle of every row, the tape holding it to the stage fell of and I had to go on stage and reattach it.When I finished taking data on speaker A, I repeated the same steps and frustrations on speaker B.

Halfway through the third night, I was finished with measurements.I then started taking data with the sound meter.I activated my equipment, and spent the next half-hour of night three and the hour and a half of night four going from seat to seat with the sound meter.I took the readings at the source (speaker A and B) once, and then at each seat.This activity turned out to be very annoying.I had to listen to a constant 220 Hz for about two hours.By the end, my ears were ringing.Nevertheless, I finished collecting my data with plenty of time before the deadline to analyze it.

Table of Contents

Data Analysis

The first thing I did with the raw data I collected is put it in a chart (appendix A).

Column A in the chart is the row and seat number of the data point.

Column B is the distance in meters from speaker A to the seat.

Column C is the distance in meters from speaker B to the seat.

Column D is the number of wavelengths from speaker A to the seat.I found this with the

formula v/f = l, where v is 343 m/s and f is 220 Hz.This gives you the wavelength emitted by the speaker.To find the number of wavelengths to the seat, I divided the distance to the seat by the wavelengths.

Column E is the number of wavelengths from speaker B to the seat.I used the same formulas

from column D.

Column F is the difference between the number of wavelengths from columns D and E.This

number tells us if it will be constructive or destructive interference.

Column G is the volume in decibels as recorded by the sound meter.

As it is, the data chart is almost unreadable.It just looks like random numbers, and is impossible to draw conclusions from without breaking it down, or arranging it.Graph One was 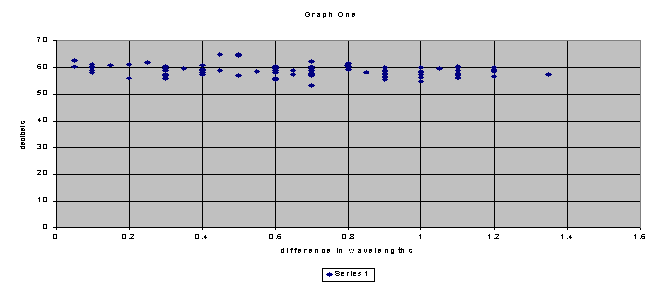my first attempt at organizing the insanity of the data.

Graph One is all the data points in columns F and G arranged from least to greatest.The x-axis is the difference in wavelengths and the y-axis is the decibel reading at that spot.After I printed Graph one, I realized that it looked wrong.According to the laws of physics, the sound should have been louder as the difference in wavelengths came to a whole number.Instead, the data points form almost a straight line, equal all the way across.Head scratching time.I was on the verge of dropping IB, when out of the blue I heard the all-inspiring words of Scotty--“You cannot change the laws of physics.”The light bulb came on.I figured out that this graph

doesn’t account for the changes in distance.In each row after the first, the sound is less due to distance from the speakers.This means that as the wavelengths get closer to one on the graph, the sound level stays the same or even goes down instead of rising.After overcoming this obstacle, I realized that the only thing Graph One would be good for, is to be framed and sold as modern art.

This is when I decided to make individual graphs of each row.These graphs made more sense because the distances from speaker to seat were similar.As the differences in wavelengths approached whole numbers, the sound rose; they followed this pattern loosely.Row A is a real stretch.In order to fit the pattern, I had to exclude about a third of the data points.After I did that, it was perfect.I drew a curved line on the graph to demonstrate the pattern.

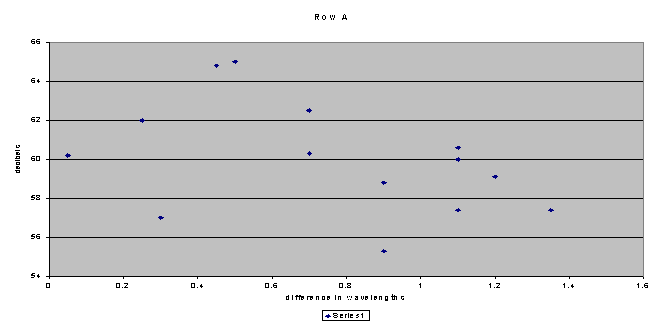
The curved line demonstrates the sound wave effect that I’m looking for.One can see that as the difference in wavelength approaches a whole number the sound meter reads a higher decibel level.Also, as the difference in wavelength moves towards a half number, the sound is less.

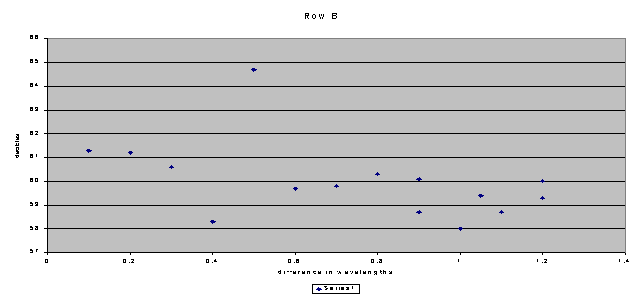
Row B is a perfect example of the idea of constructive and destructive interference.At zero on the x-axis, the graph starts out high, and lowers as it approaches .5.Then, as it goes to 1 it rises again.I drew a line to demonstrate this, and only had to exclude one data point.The reason why I excluded a data point is because it didn’t fit with the rest of the data taken.It showed a four-decibel jump where there shouldn’t be one.None of the other seats around showed a sound level that high, so I will assume that there was a problem with the equipment or the measurements from that seat.

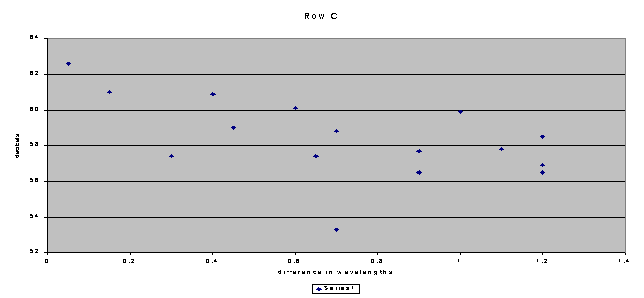
Row C loosely fits this pattern too, though it contains more widely spread decibel readings.On this graph, I drew a line to show the same pattern as the other graphs.

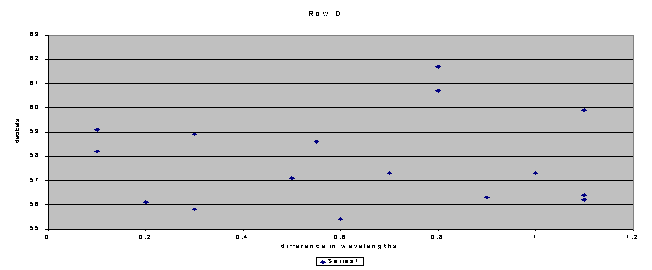
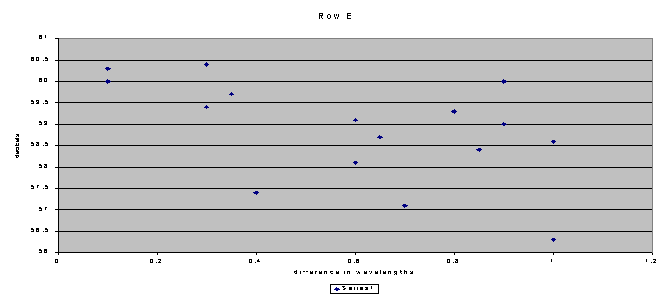
I had a hard time determining why the Row D graph turned out the way it did.Either the physics gods are out to get me, or there is something I’m not seeing.Drawing the wave pattern on this graph would be useless; I would end up excluding more data points than I include.My only possible explanation for the wackiness of this graph is that all the data points above 58 dB are sound echoes.In the seats with dB readings lower than 58, the sound meter only picked up what the speakers were emitting.On the higher dB readings, the sound meter was listening to the sound reflecting off the walls and ceiling.These echoes ended up causing constructive interference that raised the dB reading.

Row E is back to the normal pattern as most of the other graphs.I drew the curved line to represent the waves of interference.Also, in this Graph, I only had to exclude one data point.

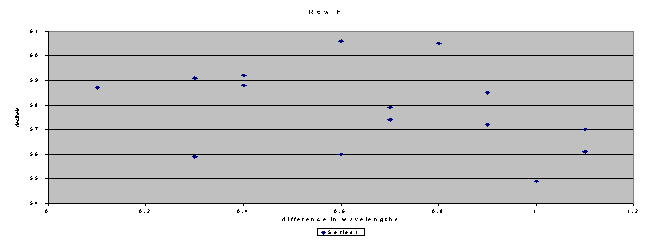
Row F’s graph came out a lot like Row E.The pattern fit, and I only excluded two data points.

With the exception of row D, all of the graphs had the curve shape I was looking for.This means that the first six rows of the auditorium fit the physics sound wave pattern. The next part of the data analysis is to graph the intensity at the constructive and destructive points.To do this, I will use an equation from Giancoli:

b(in dB) = 10 log (I/ Io) , where;

b = decibels,

I = intensity in watts/meter²

Io = minimum hearing for human (1*10^-12)

I will now solve for I to get an equation I can use:

b = 10 log (I/ Io)

b/10= log (I/ Io)

10^b/10 = I/ Io

(Io)*( 10^b/10) = I

Using this formula, I converted the decibels from my raw datato intensity, andusedthese values in an Intensity vs. distance graph.

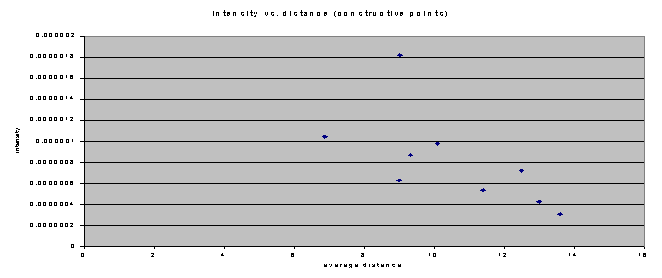
For the x-axis on this graph, I used the average distance in meters from speakers A and B to the chairs.I only used the points that had constructive interference (differences in wavelengths from 0 to .05 and from .95 to 1.05).The y-axis is the calculated intensity at that chair.From this graph, several conclusions can be drawn.One conclusion is that as the distance increases slightly, the intensity decreases dramatically.This result was expected, because the equation I used was exponential (the independent variable was in the exponent of the function).In this sense, the sound in the auditorium acted exactly how it should have.The decibel readings I took did go down as I got farther away from the sound sources, which caused the exponential decrease in the intensity.Another conclusion suggested by this graph is that if the lowering of intensity continues throughout the next few rows, by the end of the auditorium, the intensity would be almost nothing.This is a question for further study, as I have no time now to explore that possibility.

Next, I made another intensity vs. distance graph, this time using the points of destructive interference (difference in wavelength of .4 to .6).Here is the resulting graph:

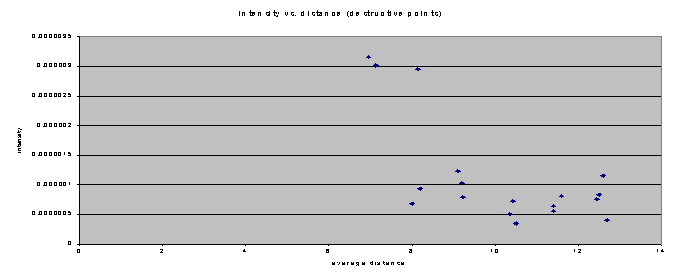
This graph turned out to be quite different from the graph of the constructive interference points.In this graph, there is no discernible exponential curve.This is because as the destructive interference points get farther away, the decibel readings remained about the same.My only explanation for this, is that while the intensity of the constructive points decreases due to distance, the destructive points have already reached their low.The intensity has nowhere to drop, so it just hovers around 5.5*10^-7 watts/meter².

Table of Contents

Conclusions

The most important thing to talk about now, before coming to any conclusions, is the uncertainty of this project.Though I tried to be as accurate as I could, parts of this investigation are riddled with uncertainties.The biggest one of these is measuring.I used an accurate tape measure, but if I didn’t hold the tape measure exactly where I held the sound meter, all the calculations would be off.This could explain why there are some data points that I had to exclude on the graphs.If one measurement in the beginning was wrong, then the whole series of equations for that data point would be wrong, thus the skewed data point.To fix this problem, I would have to retake all of my data several times to get an average that is more accurate.Even if I did this, though, the graphs would still look basically the same.There would still be a normal wave graph for all the rows, just like I have now.Another problem that I didn’t think about until after taking the data is the fact that me being in the room changed the results.When I was holding the sound meter to measure the decibels, sound waves were bouncing off me and going into the sound meter.This could have thrown off the results too.To fix this problem, I would have to build some kind of stand to hold the meter, and then retake all my data while standing away from the sound meter.Though there were a few opportunities for uncertainty, I think I did well.Almost all of my graphs had the wave pattern I was looking for, so my measurements and calculations couldn’t have been far off.

So, after spending 20 to 30 hours or more on work, of which I planned ahead and spread over the year, I now come to the conclusion portion.But what can be said about this experiment, besides the fact that it cost me numerous episodes of the Simpsons?From the data I collected, I think it would be best to sit in row C.The main reason for this, is the variance in levels of sound are very small for that whole row.You could sit anywhere in row C, according to the graph, and you would hear almost the same sound.The opposite can be said about row D.If you were sitting in D-7, you would hear about 5 dB more volume than the person in D-9 would, even though both of these seats are within one meter of each other.So, there are definitely “good” and “bad” areas to sit in the auditorium.We have to keep in mind, though, that all of this data was taken at 220 Hz, and the results would vary significantly if the frequency were changed.

Another idea that deserves another look is the results of the intensity data.I found it interesting that as the constructive interference points got further away, the intensity decreased, while the destructive interference points stayed in the same intensity range the whole time.This could mean that, by design, after the sixth row in the auditorium there would be almost no intensity change between destructive and constructive interference points.With all of the reflections of the original sound, by the back of the auditorium there would be no constructive or destructive interference; just an equal amount of the same sound.This would be a good topic for further study: to find the difference in decibel and intensity readings in the back of the auditorium.

Another thing I have thought more about since the data analysis portion is Graph One.In the eyes of a physicist, it is a bad graph.It fails to show the wave pattern it should.However, in the eyes of a sound technician it is perfect.What more could a performer ask for than an area where the sound is distributed evenly?I think this is what the architect had in mind when designing the auditorium; their specifications required even sound distribution, not a physics wave-style sound distribution.So in conclusion, according to the data points taken in the first six rows, I believe that the architects did a fairly good job designing the new auditorium.

Table of Contents

Works Cited

Berg, Richard E.The Physics of Sound.Prentice Hall.Simon and Schuster Co.

New Jersey. 1995. pp. 41-43, 219-236.

Giancoli, Douglas C.Physics. Prentice Hall. New Jersey. 1991.pp 308-333.

Knudsen, Vern O.“Architectural Acoustics”. Scientific American. November

1963. pp. 78-92.

Moore, Brian C.“Space Perception”.Psychology of Hearing. Baltimore, 1997.

Trigg, George L, ed. Encyclopedia of Applied Physics. Vol. 19.VCH publishers,

Inc. 1997.pp. 58-63.

Table of Contents

Links

http://rustam.uwp.edu/GWWM/sound_waves.html--this is a cool site about sound waves

http://www.phys.uregina.ca/classes/phys200/vibr_wave.html--this page includes a plethora of information on sound waves

http://www.glenbrook.k12.il.us/gbssci/phys/class/sound/soundtoc.html--another knowledgeable source on sound waves and their different properties

http://csgrad.cs.vt.edu/~chin/chin_sound.html--this too, is a nice site for background information

http://physstud.jmu.edu/Harrell/__sound_waves/__sound_waves.html--go here! it is about sound waves, too.

And finally, the moment you have been waiting for, the infamous "Mr. T vs Dr. Evil" site:

http://www.geocities.com/Hollywood/Club/3561/mr_t_vs_dr_evil.html-- I pity the foo'!