Ping Pong Air
Suspension
Table of Contents:
| Introduction
| Setup | Experiment
| Analysis
| Conclusion | Works Cited
|
Other Links
Return To Research
Intro
In a baseball game a hitter will frequently hit a ball into the air. And always, true to form, the ball will come back down to the ground (or fielder’s glove). This is due to the natural law of gravity. In the case of the ball, gravity is pulling the baseball to the earth with a constant force. This is due to the mass of the ball and the constant acceleration or pull of gravity (Giancoli 28). But has anyone wondered what it would take to have a baseball go up and not come down--become suspended in the air?
In order for this to occur, one would have to find an equal and opposite force to combat the force of gravity. Some forces that can counter the force of gravity are: magnetism, electric forces, and any physical application of force administered to an object so as to produce a net force greater than that of gravity acting upon it. In answer of this problem, the most abundant item around a baseball field is air. That is the most logical item for this question that could have any influence on a baseball. Since a baseball does not have many magnetic poles of energy to be arranged and it has no electric capabilities, the first two possibilities are eliminated. But before addressing the above question, several factors should be considered.
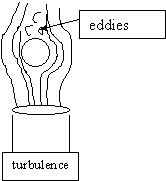
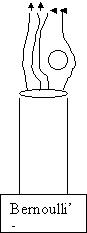
When dealing with an object moving through air (or liquid for that matter), laws of aerodynamics need to be observed. First when an air current strikes a ball, the air is forced to go around the object. In so doing, it creates low and high-pressure areas (Jischke, 250). This deflection of air creates a type of lift. The air has a higher pressure at the point where it strikes the ball and a lower pressure behind the ball as the air is going away from the object. This causes the ball to move in the direction of the lower pressure (Mises 250). In most instances this is called Bernoulli’s Principle. During the free-floating time period, the ping pong ball experiences some interesting phenomena. As the ball is floating freely over the cylinder, it occasionally drifts to the outer edge of the airflow. But once there, it is immediately pushed back into the center of the airflow as if there are invisible walls around the tube. This is due to a physical law called Bernoulli’s Principle. It states that “where the velocity of a fluid is high, the pressure is low, and where the velocity is low, the pressure is high” (Giancoli 250). So when the ball reaches the outer edge of the airflow, the air velocity is greater in the middle and lesser on the edge the ball is on. A higher pressure is created on the edge and a lower pressure is created in the middle; thus, causing the ball to seek a lower pressure in the middle of the airflow.
But as these principles
occur, another item of aerodynamics comes into play. After the air flows off the trailing edge of the ball, it runs
into the other currents and comes back on itself causing drag (Jischke
77). This drag causes the air current
to come back upon itself producing eddies
(ibid. 77). Now because we are
dealing with a simple, smooth ball, all these elements occur at a small
level. However, the item of most
interest for this project is velocity of air current.
With all these keys in mind, the topic for interrogation is based on the velocity of air versus the force of gravity on a baseball. The question of interest is what is the velocity needed to keep a ball such like a baseball (but in this case, a ping pong ball) suspended in the air? The hypothesis going into the project is that a large velocity will be needed to counteract the force of gravity on a baseball in a manner so that all forces vertically and horizontally will sum up to the value of zero.
Back to Table of Contents
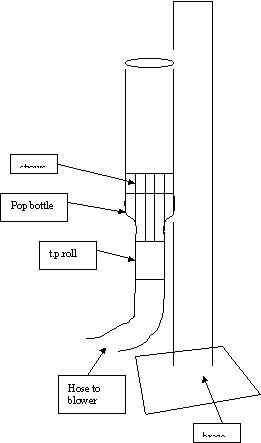
The apparatus used is a compilation modern and generic materials. The source of air current constitutes a vacuum/blower of the brand Air Source c/o Mr. Murray and the Physics Department. There is a rubber hose that runs from the vacuum/blower to a constructed end-piece uniquely called the e.j.m. deluxe nozzle. This end-piece consists of one toilet paper roll (empty), one plastic 20 oz. pop bottle (also (burp) empty), a clear fiberglass tube with the approximate dimensions of 31 cm long and 12.7cm in diameter, approximately 100 straws, and a roll of uni-cohesive bonding strip (tape). The modern materials consist of an accurate, sensitive scale and a video camera.
With a sharp knife (or in my case a pair of dull scissors) the bottom of the pop bottle was cut off and a hole was cut in the top that was approximately the size of the toilet paper roll. The toilet paper roll was attached to the pop bottle with tape. Many straws were coiled together into a cylindrical shape and fastened with tape side-by-side. The reason straws were used was so that the air coming from the vacuum/blower hose would be directed in as straight of lines as possible. This produces a constant and linear airflow which will be identified later. The resulting bunch had each end inserted into the cut off end of the pop bottle and the end of the fiberglass tube. It was fastened with the use of the universal fastening agent, yes, tape. The e.j.m. deluxe nozzle was attached to the hose by, again, tape which, in turn, was attached to the vacuum/blower (tape surprisingly not needed).
Now once attached, a keen observation was noted. Unless the nozzle was held by an individual in a perfectly vertical position, the construction would not remain upright enough to conduct any tests. This was solved by a simple brace consisting of a few boards and, you guessed it, more tape. Once the e.j.m. deluxe nozzle was vertical and securely in place, the experiment could proceed.
The first and primary objective was to find velocity since this force, in the form of flow rate, applied to the ball will be responsible for countering the force of gravity. The airflow or flow rate of the moving substance is defined as “the mass of the fluid that passes a given point per unit of time” (Giancoli 249). This is found with the help of the equation of continuity (ibid. 249). The equation is stated: pAv=pAv where p is the density of the fluid (air is 1.29kg/m3), A is the area, and v is the velocity. Force in Newtons can be substituted for one side since the flow rate is an amount of force shown by the units (kgm/sec2) on both sides. In this experiment the force applied by gravity was found by multiplying the mass of each ping pong ball (2.3g, 2.45g, 2.34g, and 2.48g respectively) by the acceleration of gravity (9.8m/sec2). For the other side, the air density is 1.29 kg/m3(Giancoli 238) and the area is pr2d or .06352p. v is the unknown. The resulting equation and solution is:
.0024(9.8)=1.29(.06352p)(.27)v
.02353=.004412155374v
v =5.33 m/s
To check this answer, a video camera was set up to record the motions of the ping pong ball in the air current. A meter stick was placed next to it to record the height at which the ping pong ball travels. By manipulating an air intake valve on the vacuum/blower, the ball was made to come to a rest at the bottom of the nozzle. The valve was then immediately closed and the ball rocketed up. In reviewing the video of the experiment and slowing it down frame by frame, the height and time were obtained since each frame constituted 1/16th of a second. These measurements were then put into equations such as v = u+at and the results supported the conclusion of approximately 5.33 m/s. Results are further tabulated in the Analysis section.
By applying the formula v=u+at to each of the experiments on each ball, the following results were obtained:
|
Trial V=u+at |
Ball 1 (.0023kg) |
Ball 2 (.00245kg) |
Ball 3 (.00234kg) |
Ball 4 (.00248kg) |
||
|
Average Time |
.5 sec. |
.5 sec. |
.5 sec. |
.5625 sec. |
||
|
Acceleration(m/s2) |
-9.8 |
-9.8 |
-9.8 |
-9.8 |
||
|
Final velocity m/s |
0 |
0 |
0 |
0 |
||
|
Initial velocity m/s |
4.9 m/s |
4.9 m/s |
4.9 m/s |
5.5125 m/s |
||
|
|
||||||
| Data File for above table | ||||||
From the results in the ping pong experiment, one can easily take and apply them to the original baseball question. This can be done with a simple ratio. For example, the velocity needed to suspend a .0023kg ball is 5.33m/s or .0023/5.33. To apply it to a .2778kg baseball, a simple proportion can be created.
.0023/5.33=.2778/v
v=644.7m/s
While these figures are not nearly as accurate as the calculations in the previous section, they offer a reliable check point to see if the solutions from above are in the same ballpark (pun intended).
During much thoughtful reflection, some interesting behaviors were noted during experimentation. Since the force created by the velocity of air is constant only until the point it leaves the tube, it was realized that if the ball floated at any substantial height above the tube, another factor would have to be taken into consideration. As the airflow collides with the atmospheric air of its surroundings, the force diminishes at an increasing rate. Thus, the velocity, and thus force of the air, of the air would be considerably less at a height of, say, 5cm above the opening of the tube. Had this situation arisen a decreasing amount of the flow rate would be needed.
During this experiment, many factors could have attributed to errors. First, the equipment used was not the most accurate. This is seen in the simple and generic materials used to perform said experiment. Next, human error is always present in both measurements taken and calculations of equations, etc. Finally, the amount of trials and different methods could have been increased to obtain more accurate, reoccurring data. However, all methods were performed to the best of this human’s ability.
Now, because a baseball is quite different from a ping pong ball, the actual force requirement will be slightly different from these conclusions. However, due to the fact that the differences only hamper the ability to suspend the baseball, the concluding figures represent the absolute minimal force required to have this phenomena occur. In short and in support of my hypothesis, the best chances of having a baseball go up in the air and not come down would be to have a mini mega-tornado affect it with equal wind velocities and factors as observed in this experiment
Clarke,
Donald. Science and Invention, Vol.1. pgs. 26-33,43-44.
Giancoli,
Douglas. Physics. Pgs. 244-255.
New Jersey: Prentice Hall
Int., 1980.
Jischke,
Martin. “Aeronautics”.
World Book Encyclopedia Vol. 1.
pgs. 75-78.
Lorimer,
Lawerence and Costagno, Joseph.
The New Book of Popular Science,
Mises,
Richard. Theory of Flight. New
York: Dover Publications, Inc.,
1959.
Schneider,
Herman and Schneider, Leo. “Aerodynamics”
Scinence in Everyday
Wald,
Renee. Tuhs.ttsd.k12.or.us/Departments/Science/Physics/Research/
For more information on this topic or similar applications of these properties, look in aerodynamic sites.
If you have any physics-related questions this website will answer them all.
For a closer look at the aerodynamics of a ping pong ball, there are some tutorials.
For in-depth coverage of aerodynamic properties use your brain and this website.
A good source of computer programs for airfoil analysis would be this site.