A Study of Force of Friction

David Baumer

Introduction | Statement of Problem | Review of the Related Literature | Statement of Hypothesis | Method | Results of Trial 1 | Graph of Data of Trial 1 | Results of Trial 2 | Graph of Data of Trial 2 | Discussion | Conclusion | Works Cited | Related Links |               Return to Research Projects

Introduction | Table of Contents

Force plays an important role in physics, as it’s involved in many different areas of physics. One type of force is the friction force. Friction force is defined by Dr. Lamott, from Concordia University, St. Paul, Minnesota, as the "force created between two contacting surfaces that tend to rub or slide past each other" (Lamott). The ability for an object to slide on any surface depends upon several factors. These include texture of both surfaces, how much force is pressing on the surfaces, the presence of a lubricant, and the contact area, including both the surface upon surface contact, as well as the microscopic contact areas. To calculate the force of friction, the normal force is multiplied by the coefficient of friction. The coefficient of friction can also be described by dividing Force of Friction by The Normal Force. Two formulas:

F_Fr=m _SF_N m _S= F_Fr/F_N

The coefficient of friction depends on the texture and hardness of the two surfaces rubbing together. Two coefficients exist when calculating the friction force. These are the coefficient of static friction, and the coefficient of kinetic friction, with the former being smaller. In this experiment, the coefficient of static friction will be explored. The coefficient of static friction is the coefficient of friction for "two surfaces that tend to slide under the influence of some motive force but have not yet begun to move" (Lamott).

Statement of the Problem | Table of Contents

The problem presented is to determine whether the coefficient of static friction depends on the time a force is applied to the block before pulled on, and if the coefficients are different based on materials used.

Review of Related Literature | Table of Contents

Galileo interpreted friction force as a force to slow an object down. He likened friction to pushing or pulling on an object to slowing it down or speeding it up. He then determined the basis that is evident in Newton’s 1^st Law of Motion, which states that everything "continues . . . in a straight line unless it is compelled to change that state by a new force acting on it," for example, friction force (Giancoli 67). Another interpretation can be that "every body perseveres in its state of being at rest or of moving uniformly straight forward, except insofar as it is compelled to change its state by forces impressed on it," or in more plain language, "things that are standing still tend to stand still, unless you push on them hard" (Gleick 29).

Newton’s 2^nd Law of Motion involves acceleration, stating that it is "directly proportional to the net force acting on it and is inversely proportional to its mass. The direction of the acceleration is in the direction of the applied net force" (Giancoli 69). One other source stated that Newton’s 1^st and 2^nd Laws of Motion can be summarized as: F=ma, or Force equals the mass of an object multiplied by its acceleration (Podesta 17). One source notes that the mass, or sometimes called the inertial mass, is the same as the "quantity that measures the ability of an object to produce (or react to) a gravitational field (Davies 70).

Friction has many valuable uses, including keeping a car on a road, stopping a car, or standing something up without it sliding around; yet it can also reduce the efficiency involving many other uses (Sieck).

The coefficient of friction very much depends on the materials of the two items, the block, and the surface, as well as the cleanliness of the contacting surface. It does not depend on the size or shape of the contact surface (Lerner 418).

One must note that friction does exist between two solid surfaces, even if not evident at first glance, as discussed earlier involving the contact areas. This is because even the smoothest looking surface is quite rough when looking at it microscopically (Giancoli 69). When two solids are pushed against each other, contact occurs between the microscopic peaks of the objects.

Statement of Hypothesis | Table of Contents

The hypothesis presented is that the coefficient of friction will depend on, and increase in proportion to, not only the obvious object-to-object contact, but on the time the weight puts force on the block as well. To determine this, I will pour sand into a small cup that is set in a pulley system until the object moves and measure the mass of the sand and cup. Then I will use this mass and the mass of the block to calculate the Normal Force and Applied Force. Then, using the formula presented above, calculate the Coefficient of Static Friction. I will do these calculations for Wood on Wood, and then for Polymer on Polymer.

Method | Table of Contents

Originally, I planned to use a force meter to pull on a block on the table, but this leaves too much room for uncertainty. The better plan, and the one that I finally settled on, called for a pulley system.

Before completely setting up the pulley system, I had to put together the items that would be used by the pulley system. First, I placed a nail in a piece of pinewood, and folded the nail over to make a hook.

Then, I drilled two holes in the top of a 16-oz. plastic cup, and strung a string approximately 60 cm long through the holes, tying a knot part way up the string, to form a hanging cup like this:

Originally, I had planned to use a small, 4-oz. cup, but in performing the first trial, I discovered that it would not be large enough to perform the whole experiment, hence the new, 16-oz. cup. Next, I put the two pieces together, stringing the string around the nail-hook, putting the two pieces together.

Next, I clamped the pulley on the table, draped the string over the edge of the pulley on the table:

I marked the string with a black marking pen so I knew where to place the string at all times. This would reduce the chance of uncertainty in the experiment because the string would be the same distances from the edge of the table to the block each trial.

After I had the apparatus set up, I gathered all the other necessary items to start the experiment. I needed an ample amount of sand, a means of putting the sand into the cup, and a considerably large weight to weigh down the block:

I planned to sit a 6-kg. weight on the block for a certain amount of time, and then pour the sand into the cup until the block moved. The data taken would be the mass needed to move the block for 0-20 minutes, in increments of one minute. I ran into problems concerning the time, which will be discussed at a later time.

I ended up performing this first experiment over the course of two days. The first day, I measured the data for the first 11 increments, from 0-10 minutes each. The first trial, I placed the block on the table, lined up the string at the black mark, and then proceeded to slowly spoon the sand into the cup. I tried to comb the sand out of the spoon as slowly as possible, to get an accurate measurement. Then, when the block started to move, I would mass the cup with the sand in it, and record the data. I then emptied the cup, and placed the block and cup back on the pulley system. Next, I placed the 6-kg. weight on top of the block, and let it sit on the block for 1 minute. At the 1-minute mark, I removed the weight, careful not to move the block to the best of my ability, and continued to slowly put the sand into the cup as discussed before. I repeated this nine more times, for two minutes, three minutes, in procession up to ten minutes.

The next day, I proceeded to pick up where I had left of the previous day, but I had already altered my plan. To take data for the times of 11-20, on every minute would take around 150 minutes, or about 2.5 more hours. I hypothesized at this point that we could estimate the values for the odd minutes (11, 13, 15, 17, 19) by taking data for the even minutes (12, 14, 16, 18, 20), so I decided to proceed by only taking the data for the even minutes. The results of this hypothesis will be discussed later.

For the second trial, I wrapped the wood block used in the first trial in a plastic, transparent book cover. Then, I placed it on a Formica shelf, and set up the pulley system like the first trial, on the edge of the table. I used the same sand and cup system as the first trial, as well, so the only variant was the wood on table connection, pr. this time, a polymer on a polymer. This time, however, I took data for the even times only, as that is what I would end up doing with the first trial.

Results of First Trial | Table of Contents

As I massed the cup after each step, I recorded the data and arranged it in the following chart:

I encountered some problems in recording the data. If you notice, the listed data points are only for the even minutes (2,4,6,8,10,12,14,16,18,20 minutes). I had planned to do 0-10, all the minutes, and then 12-20, even minutes. The highest recorded value in the mass column for the first 10 minutes was .140 kg, at the 10-minute mark. However, when I proceeded to experiment the next day, I recorded a value of .644 kg at the 12-minute mark. This mystified me in thinking about the large jump between 10 and 12 minutes. I then decided that this could not be an accurate result. I had two ideas: 1) The .644 kg was notably large, or 2) the previous eleven values were notably small. I then decided that I was going to essentially start over with the experiment, but alter the procedure in a minor way. I decided to re-measure the values for the minutes 0-20, with only taking data for the even minutes (see above). This data was finalized in the chart above. The numbers were somewhat larger than the recorded values from the day before, showing that a bit of chance may be involved in the experiment. These numbers looked suspicious to me, as they were not following my hypotheses, which is a very strong possibility in science since our experiments sometimes lead us away from our hypotheses.

The next step was to finalize the data and calculate the coefficient of friction. To do this, we need to recall the equations given earlier:

F_Fr=m _SF_N m _S= F_Fr/F_N

I used the second equation, which reads: the coefficient of static friction equals the Force of Friction, or Applied Force, divided by the Normal Force, or the Weight of the object. To do the necessary calculations, I needed to find the Weight and Applied Force. The Weight of the object can be summarized as the force needed to hold the block to the table, and can be calculated by multiplying the mass of the block by the acceleration of gravity, 9.8 m/s². The Applied Force can be summarized as the force needed to move that block from its stationary state.

I can take the time and mass for 0 minutes, for example. The mass of the block was measured as .25 kg. Find the Weight:

.25 kg * 9.8 m/s² = 2.45 N

Next, find the Applied Force for 0 seconds:

Mass * 9.8 = .102 * 9.8 = .9996 = 1.00 N

The calculations for all of the trials can be summarized in the chart below:

As we can see, the Applied Forces have been rounded to two decimal places for a more pleasant look.

Now I had all the components necessary to calculate the Coefficient of Static Friction of Wood on Wood. Let’s recall the formula to do the calculation once again:

m _S= F_Fr/F_N

We know the Force of Friction and the Normal Force, which are the Applied Force and Weight, respectively, from the charts above. The calculations resulted in the following chart:

The average coefficient of friction determined from the experiment is .76. The larger values of the coefficients mean that the pinewood block has a stronger connection with the oak table. For example, the final four time intervals have a pretty strong connection. A problem occurs at the 840-second time interval, however. The coefficient of friction is larger than 1.00. If a coefficient of friction is larger than 1.00, this means that the object will probably not disconnect from the surface it is placed on. This is not the case, however, with the block, since the data was taken when the block moved. Perhaps, when I was pouring the sand into the cup, I could have poured an extra amount of sand into the cup as it was falling.

Next, I placed the data from the chart into a graph, with the Time on the x-axis, and the Coefficient of Friction on the y-axis. This is viewed in the following graph:

Table of Contents

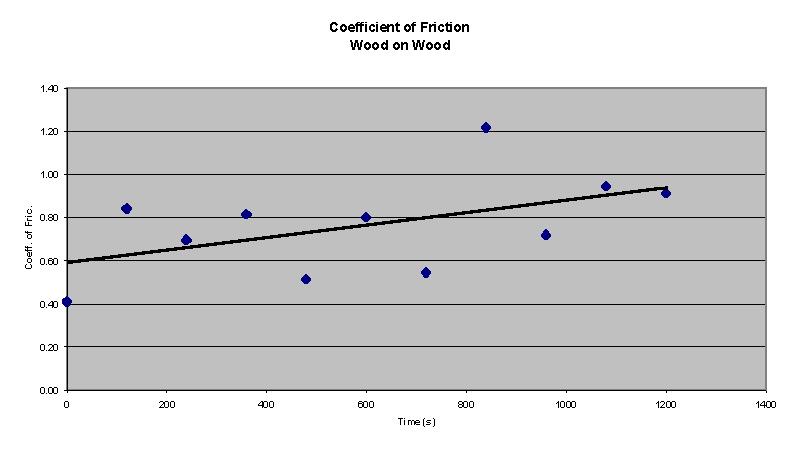
Data1.txt | Data2.txt | Data3.txt - These 3 Data files contain the data used to make the above graph, the exact figures for the graph come from Data3.txt

The blue dots on the graph represent the data points from the data table above. As we can see, however, the data does not present a reasonable pattern. Instead of connecting the data points I have derived an equation for a best-fit line for the data. This line can be used to determine, given a specific time, the approximate value for the coefficient of friction to move the block after it has been covered by the weight for that specific amount of time.

We can take a look at the overall uncertainty, in the following tables. First, we can look at the time and the experimental value:

From putting the data in my TI-86 Graphing Calculator, the equation of the line, where x is the time in seconds, has been calculated approximately:

Y = .592 + ((2.87x10^-4) * x)

Using this equation, the coefficients of friction are calculated, and listed with the previous chart in the following table, where the exp. stands for experimental value, and the calc. stands for calculated value:

Now, we can take this a step further, and calculate the overall uncertainty between the data points, and the graph itself. This can be seen in the following data table:

We can see the average uncertainty between the calculated value from the regression line and the experimental values is +.32. That means that the calculated values for the coefficients were, on the average, .32 more than the experimental versions. The most uncertain point is the point for 840 seconds. This coincides with the fact that the experimental point is impossible since the coefficient of friction cannot be larger than 1.00, or the item may not move, as stated earlier. The values for 1200 seconds, and 240 seconds are the least uncertain points in the chart. As will be discussed later, these are probably just chance values.

Results of Second Trial | Table of Contents

Before the second trial, I hypothesized that the uncertainty of the second trial data would be smaller, since the two interacting items were smoother, so the bonds would be more numerous, but not as strong.

As I massed the cup after each step, I recorded the data once again and arranged it in the following chart:

The next step was to finalize the data and calculate the coefficient of friction. To do this, we need to recall the equations given earlier:

F_Fr=m _SF_N m _S= F_Fr/F_N

I used the second equation again, and calculated the Applied Force of each time interval, and can be summarized in the following chart:

As we can see, the Applied Forces have been rounded to two decimal places for a more pleasant look.

Now I could calculate the Coefficient of Static Friction of a Polymer on a Polymer. Let’s recall the formula to do the calculation once again:

m _S= F_Fr/F_N

We know the Force of Friction and the Normal Force, which are the Applied Force and Weight, respectively, from the charts above. The calculations resulted in the following chart:

The average coefficient of friction determined from the experiment is .53. The larger values of the coefficients mean that the plastic-covered block has a stronger connection with the Formica shelf. The data is a fairly good set of data in that none of the calculated coefficients are greater than 1.00, and the range is very small. If u can recall, if a coefficient of friction is larger than 1.00, this means that the object will probably not disconnect from the surface it is placed on.

Next, I placed the data from the chart into a graph, with the Time on the x-axis, and the Coefficient of Friction on the y-axis. This is viewed in the graph below:

Table of Contents

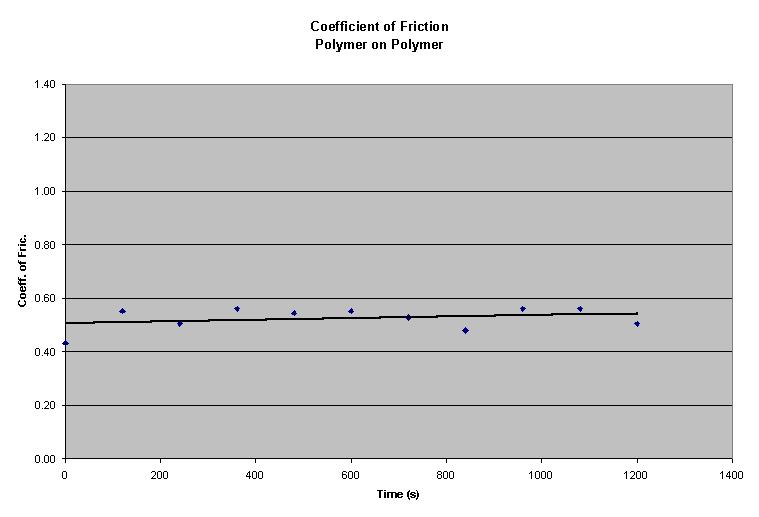
Data4.txt | Data5.txt | Data6.txt - These 3 Data files contain the data used to make the above graph, the exact figures for the graph come from Data5.txt

The blue dots on the graph represent the data points from the data table above. As we can see, the data presents a somewhat reasonable pattern, but is not completely straight. Instead of connecting the data points I have derived an equation for a best-fit line for the data. This line can be used to determine, given a specific time, the approximate value for the coefficient of friction to move the block after it has been covered by the weight for that specific amount of time.

We can take a look at the overall uncertainty, in the following tables. First, we can look at the time, and the experimental value, in the following table:

From putting the data in my calculator once again, the equation line, where x is the time, has been calculated approximately:

Y = .505 + ((3.03x10^-5) * x)

Using this equation, the coefficients of friction are calculated, and listed with the previous chart in the following table, where the exp. stands for experimental value, and the calc. stands for calculated value:

Now, we can take this a step further, and calculate the overall uncertainty between the data points, and the graph itself. This can be seen in the following data table:

Looking at this data, compared to the data for the first trial, the uncertainty is much smaller with this trial. The uncertainty of this trial is +.06, which means that, on the average, the calculated values are .06 greater than the actual experimental value. The most uncertain point is the point for 0 seconds. This could be due to the fact that the block was sitting on the shelf for an undetermined time before the data was taken, or it could be a considerably low number. The most certain point is for 720 seconds, which is calculated exactly at two decimal points. Overall, the experimental points for the second trial are much more certain than the experimental points for the first trial, which is discussed below.

One more thing I looked at was the comparison between the uncertainty of both trials versus each other, with the first trial as T1, and the second trial as T2, and is produced in the following chart:

Looking at the data, the average uncertainty for the time intervals ranged from .01 to .17, with the average uncertainty of .19. The most certain point was for 240, 1080, and 1200 seconds, which were also three of the most certain points in the both trials. The least certain time interval was for 840 seconds, which also happened to be the largest uncertainty in the first trial. The .17 uncertainty is not very large, but the low uncertainties are due to the first trial uncertainties. So, perhaps the average uncertainty should not be looked at, but instead, we should look at the most and least certain points in each chart separately.

Discussion | Table of Contents

Looking at the first data table once again, I have the one value that is over 1.00, which cannot be a real value. Perhaps, then, we can find the largest mass of sand + cup possible to have the largest coefficient of friction, as the coefficient approaches 1.00.

Let’s recall the formula:

F_Fr=m _SF_N

Then, we know the values for and m _S and F_N, which are 1.00, the largest possible value, and 2.45 N, the weight of the block, respectively. Therefore, the largest supposed Applied Force possible to move the block is:

1.0 * 2.45 N= 2.45 N

Then, we can calculate the largest mass value that should be needed to pull the block from its stationary point, using the formula:

F_N = m * a = 2.45 N = m * 9.80 = 2.45/9.80 = m = .250 kg

Therefore, the greatest value that should be needed to pull the block from its stationary point is .25 kg. This is true for both trials. This explains why the value for 840 seconds, which is .304 kg, is too large. This could be due to a couple of reasons. First, when the block moved, I may have dumped some extra sand into the cup while it fell, or, the scale could not have been configured correctly, or, there could have been another outside force of some kind acting on the block on that particular trial.

Conclusion | Table of Contents

Now we can recall, I had formed three hypotheses. The first hypothesis presented was that the coefficient of friction will depend on, and increase in proportion to, not only the obvious object-to-object contact, but on the time the weight is on the block as well. This, as proven, was somewhat untrue due to the first trial. The numbers are random enough that I can conclude that the value for the coefficient of friction for any given time is somewhat random. However, the general shape of the graph increases as the time increases. The coefficient uncertainty of .32 is rather large to make a concrete conclusion that the coefficient would directly depend on the time the weight is on the block.

The second hypothesis I presented that we could estimate the values for the odd minutes (11, 13, 15, 17, 19) by taking data for the even minutes (12, 14, 16, 18, 20). This hypothesis failed as well. Looking at the original graph, we can see that the original data points did not provide a clean enough graph to predict the odd minute values. Now, we could predict the values using the linear regression line, but then we would have the .32 uncertainty, and that would not be a certain enough value to depend on. However, in the second trial, this hypothesis may be somewhat true. Looking at the uncertainty of just .06, we may be able to use the linear regression line to help predict those values for the odd minute intervals. This could perhaps be an extension to this project, to decide whether this hypothesis could be accepted or rejected, by performing the experiment for those times.

The third hypothesis was that the second trial would be more certain than the first trial. I can accept this hypothesis, as the data proves. The second experiment perhaps produced better results because it was modeled after the first experiment.

I wanted to conclude because of my first experiment that the coefficient of friction does not completely depend on the amount of time a force is being applied. This action may play a factor in the coefficient calculated, but it was not thoroughly evident throughout my first experiment. This could have been due to the fact that I performed the experience over the course of 2 days, or the fact that the time does not matter in applying a force. Also, when the weight was removed from the block, the block may have been nudged, therefore the bonds have been partially broken. This could provide an uncertainty in the results as well. But, due to my second experiment, I can reform my first hypothesis to read: The coefficient of friction depends on the object-to-object contact and the time that the weight is placed on the block.

There are probably many ways to perform this experiment to get better results. For example, instead of using a large weight, perhaps, a smaller, easier to use weight of some kind could be used to put the Applied Force on the block. Since the bonds could have been partially broken when I removed the weight, the weight would be easier to take off, therefore, the results would be more certain. Perhaps the results would be more certain if more data points were taken, maybe using 0-20, with all minute intervals giving data. As well, doing two or three days worth of the same amount of trials of each object-to-object contact would give a wider range to draw from in calculating the data and forming a conclusion. The graph would have a more certain shape, and the linear regression would provide less uncertainty in the calculations. Although this may provide a more certain graph, the absolute certainty that the coefficient of friction depends on the time of the force applied would never be certain enough.

Works Cited | Table of Contents

Davies, Paul, Ed. The New Physics. Cambridge University Press, New York, NY, 1989.

Giancoli, Douglas C. Physics, 3rd ed. Prentice Hall, Englewood, Cliffs, NJ, 1991.

Gleick, James. Genius: The Life and Science of Richard Feynman. Pantheon Books, New York, NY, 1992.

Lamott, Dr. Eric E. "Frictional Force." www.csp.edu/csp/people/lamott/khs473/Friction/index.html

Lerner, Rita G. and George L. Trigs, Ed. Encyclopedia of Physics, 2nd ed. VCH Publishers Inc., New York, NY, 1991.

Podesta, Michael de. Understanding the Properties of Matter. Taylor and Francis, Bristol, PA, 1996.

Sieck, Mr. Ed. "Friction." www.esu10.org/~lexington/LexSchools/buildings/High/Science/Physics/friction.html

Related Links | Table of Contents

http://tuhsphysics.ttsd.k12.or.us/Physics/Physics.html - This is the link to the home of the Tualatin High School Physics Web Page.

http://www.ruf.rice.edu/~sandyb/Lessons/friction.htm - This is where the question What is Friction? is answered.

http://www.trms.ga.net/~jtucker/lessons/sc/simplemachine/force.html - This is another short explanation of Force of Friction.

http://mu.mae.cornell.edu/ - Here is another site that contains other related links.

http://www.educationcenter.org/friction.html - Here is a link to a page with a simple experiment to study Force and Coefficient of Friction.

http://fermi.bgsu.edu/~stoner/p201/equil1/tsld001.htm - Here is a site that contains a slide show about Friction and Equilibrium.