The Introduction

There are essentially two types of musical instruments in the world today: those that are constructed with a resonator and a continuous energy source and those that are simply a resonator. Only these two instrument types have emerged, and they basically fall into the categories of percussion and the rest of the instruments. To clarify, a drum is simply a resonator because its sound comes from the vibrations it makes only when it is struck. Another type of instrument, however, has a continuos source of vibrating energy, such as a column of air in an oboe or the bowed string of a cello.

A stringed instrument has two parts: the strings and the sound box to which the strings are attached. This sound box, or body, must resonate with the vibrations of the strings in order to produce a loud enough tone for a concert performance because without that amplification, a string’s vibrations are not powerful at all. As it is, even with the soundbox, a stringed instrument (or any instrument, for that matter) is only a little more than one percent energy efficient in terms of the energy input from the musician. At full blast, a full symphonic orchestra such as one that you would pay outrageous amounts to hear only puts out approximately 67 Watts of sound. This is why the passive resonant amplifier, the instrument body, is so important.

However, the stringed instrument is typically only made out of two types of material: spruce tree for the front, or belly, and maple for the rest of the body. This means that between those two materials, there are only two natural resonant frequencies. This brings up the question: how does the stringed instrument resonate over such a wide range of frequencies with only two natural resonances? This question is the key to all stringed instrument making, and is what makes a Stradivarius or Guarneri instrument worth up to one and a half million dollars.

Through the centuries of instrument making, a process of musical natural selection has taken place. Hundreds of instruments, many of them almost exactly like today’s instruments save for a few details, have gone the way of the buffalo. A critical factor in the success of some instruments over others has been resonance. An instrument’s resonance affects not only the volume of sound it is able to produce, but also the quality of sound. This quality of sound is called timbre, and naturally since it is a French word, it cannot be pronounced in a logical manner, but must be pronounced like TAMBER. Anyway, the timbre of an instrument is determined largely by the resonance of various overtones on a frequency, and today’s instruments have managed to create a fairly uniform timbre for all the frequencies within its range. So, the two main factors in judging an instruments value, volume of sound and timbre, are both largely dependent on resonance, and are the keys to why the musical world has placed on the pedestal the bright and powerful Stradivarius instruments.

How does one make a successful stringed instrument? Well, in such questions one usually must defer to an accomplished violin maker, or luthier, as they like to call themselves, although this paper is capable of setting forth the general concepts. First of all, the volume of sound is produced mainly by the surface area of the sound box. With more surface area of wood that resonates, the vibrations move more air molecules, which becomes louder music to one’s ears. Other factors exist, of course, such as the flexibility of the wood, but the loudness of a sound is relatively easily explained, and so the focus of this paper refers to the timbre of a stringed instrument. How does an instrument create its consistent timbre over such a broad range of frequencies?

This question has been much examined already by professional scientists, with some of the most interesting research done by Ernst Chladni (1756-1827), who discovered that certain frequencies caused correlating sand patterns on an aluminum plate. Chladni is called ‘the father of acoustics’ for his study into how sound affects physical matter. In modern day times, the late Dr. Hans Jenny of Switzerland has expanded Chladni’s experiments into a branch of science called cymatics, which is the study of how vibrations generate and influence patterns, shapes, and moving processes.

The application of this research to the present paper is found mainly in the Chladni patterns and their ability to recreate themselves on the front and back plates of a stringed instrument. It has been shown that with certain frequencies, there are different modes, or patterns, of vibration on the stringed instrument. These patterns show how the masterful design of a stringed instrument allows the body to resonate in a symmetrical manner with different frequencies. The symmetry, in theory, assists the consistency of timbre through the instrument’s range.

Regarding the hypothesis of this paper, I have examined the resonance patterns described by the Chladni patterns using a cello, but instead of using sand, which falls off the cello's sloped back plate, I am using a contact microphone. I expect to find that, since Chladni shows that various places on an instrument resonate differently than others, the microphone will pick up different dominant frequency vibrations from various places on the cello while the same note is played on the string. I would further postulate that the vibrations which tend to the low side of the note being played will be found on both sides of the cello, as will the higher frequency vibrations, in order to maintain the symmetry. A computer program called Spectogram, taken from the internet, reads and graphically shows the frequencies picked up by the microphone.

Works Consulted

Construction [of a violin]. In Violin Making by Hans Johansson [online]. Cited 1999-01-
    15. Available from World Wide Web: URL:http://www.centrum.is/hansi/construction/

Cymatics- The Science of the Future? In Publication for the Expansion of Consciousness [online]. Cited    1999-01-16. Available from World Wide Web: URL:http://www.alphaomega.se/english/cymatics.html

Ernst Florens Friedrich Chladni. In Vanguard Sciences and the Keelynet [online]. 1990-

Hall, 1991. p. 316.

Jourdain, Robert. Music, the Brain, and Ecstasy: How Music Captures Our Imagination.

New York: Avon Books, 1998. pp. 30-46.

SEIFE, Charles, Cooking up the Recipe for a Modern Stradivarius. In New Scientist

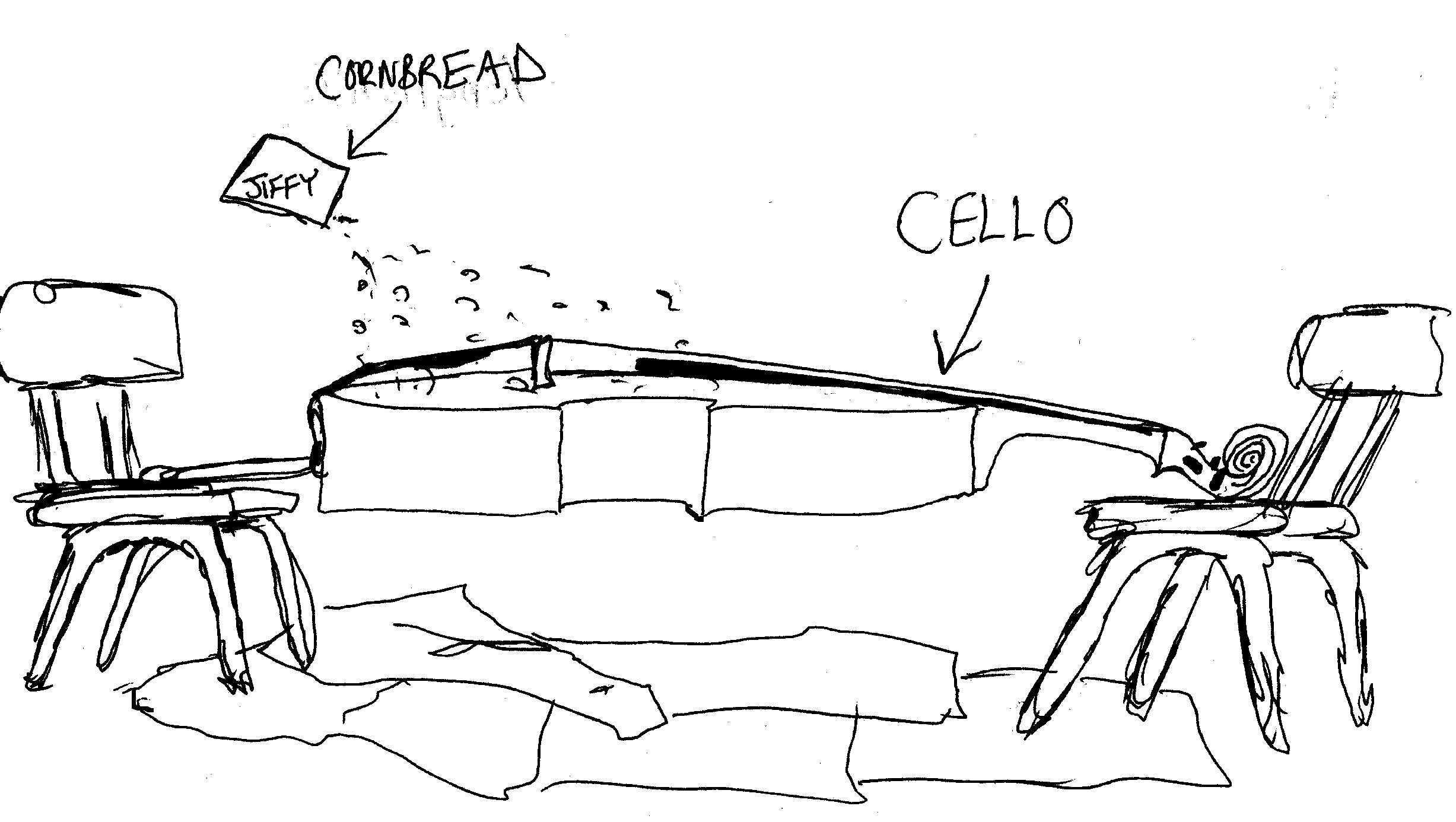
The experiment began with a cello, a bow, and some cornbread mix. The mix was intended to create Chladni patterns on the cello’s backside while the bow was creating the vibration. However, due to the reluctance of the mix to move unless forced to slide down the slope of the wood, this first attempt did not work. The force of gravity on an inclined plane was too great for the experiment to work, although several alternatives were tested. First, flour instead of the cornbread mix, but flour proved to be too sticky. Sugar, a substance more like the black sand shown in internet photos of the same process, also could not overcome gravity. I thought of using a violin because it’s backside does not have the amount of slope that a cello does, but at that point I was ready to try other ideas.
 
 

My dad had the idea of using a microphone; that way, instead of making the vibrations come to me, I went to the vibrations themselves, so to speak. Rigging the microphone with a suction cup insulator, resonant vibrations could be picked up by the computer and measured, thanks to a program off of the internet called Spectrogram. This program reads all the audio data in a resonance point, including noise and, most importantly, overtones while at the same time showing on a graph the intensity of each overtone. A redder coloring of the tone on the graph indicates a more intense, more dominant tone. The printout that follows this section is from Spectogram and it depicts the open strings of the cello being plucked in succession, first from highest to lowest beginning with A 44o Hz, down through D, G, and C two octaves below middle C. Those are the first four tones on the printout, then the order of the strings that are plucked changes.

Here is a picture of the microphone that was used to record the sound while attached to the body of the cello:

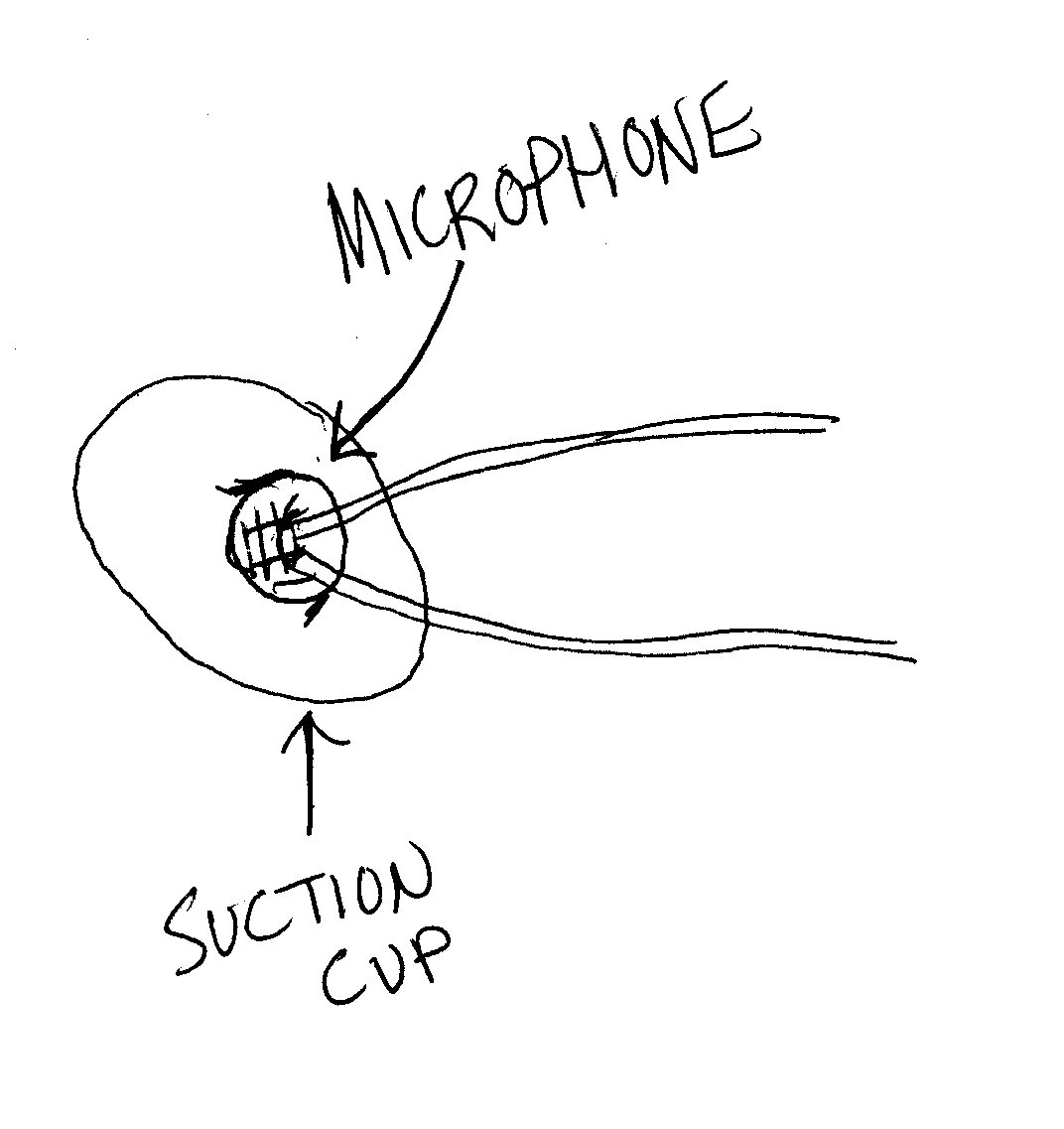
In deciding where to place the microphone for the best sampling of resonances, I chose five obvious strategic locations on both the front and back of the cello: the four corners and the center. I based this on the Chladni patterns that I found on the internet, four of which you can see on page 7. Most of the patterns on the stringed instruments involved either the center or the corners as nodes, so I assumed those to be important locations.

I then used the frequencies of the open strings, since they were easy to calculate using the table from Giancoli, seen below, and also because I didn’t have to worry about if I was playing a note consistently when pressing down a finger. I also plucked the strings to get the vibrations, because then I could fit more into a window on the spectrogram and have more frequencies to compare in a single trial.

Table 12-3

(Giancoli, pg. 316)

Note Frequency (Hz)

C                     262                                          Note: When referring to the bass and treble side

C# or Dflat     277                                                         of the cello, I mean the left or right half

D                     294                                                         which corresponds to the lower two bass

D# or Eflat     311                                                          strings or upper two strings.

E                     330

F                     349

F# or Gflat     370

G                     392

G# or Aflat     415

A                     440

A# or Bflat     466

B                     494

C’                     524

The Results

Even with fascinating technology, there is uncertainty. There are two main likely culprits of uncertainty in this experiment., and the first is found in Spectrogram. The program gives an uncertainty of +/- 5.4 Hz in its reading of the frequency input form the microphone. However, this is a minor uncertainty that is easily accounted and goes hand in hand with the variance of the strings from a tone of exactly 440 Hz. The uncertainty in this regard was diminished by a good tuning of the cello before the experiment, but such an inaccuracy is still worth considering, in my opinion.

The second source uncertainty is interference caused by the lingering tone of each open string and the next note. Of course, a plucked open string has the tendency to vibrate a lot, even when one tries to dampen it before another string is plucked. In some cases, an overtone did carry into the next note’s frequency band; however, the overtones that carried were always dominant ones and usually sounded intensely without help from the previous note.

 Click Here for some RAW data!!!!!!

The Discussion

At first, it was tempting to compare the Chladni pattern photos I found on the internet to the data from the experiment, but then I realized that the internet photos were taken of violins, a totally different animal in terms of resonance frequencies than the cello. So I looked at my graphs and realized something from the lack of support that they provided to my hypothesis. Before the experiment, I thought that symmetry would aid the consistency of the cello’s timbre from its high notes to its lowest note. But the results have made me rethink my assertion, and I now believe that the resonance patterns can probably be asymmetrical as well as symmetrical, even though the photos from the internet of the Chladni patterns show symmetrical patterns. I think that the asymmetry of the instrument’s resonance is what necessitates a bass pole and a sound post in the interior of the cello. The bass pole and sound post balance out the bass and treble frequencies, respectively, between the two sides of the cello. Both are situated basically right underneath the bridge, which is the piece of wood that communicates the vibrations of the strings to the soundbox first.

I was correct in saying that the microphone would pick up dominant frequencies. All the frequencies except two were multiples of a low frequency fundamental, usually the pitch one octave below the string that was being played. The front plate contained the exception, which was a 489 Hz frequency recorded at all corners. Still, it is close enough to a multiple of five and an octave below G that I think uncertainty covers the data.

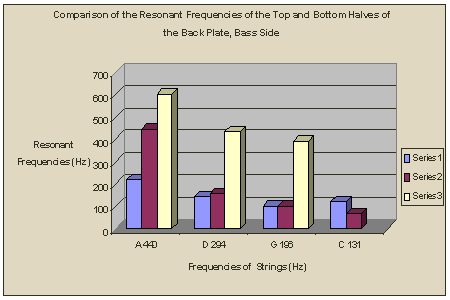
Some of the data does support the notion that certain parts of the cello resonate more with certain types of frequencies. For example, in the graph endlessly titled, "Comparison of the Resonant Frequencies of the Top and the Bottom Halves of the Back Plate, Bass Side," there is a marked trend. At the frequency of A 440 Hz, the top half of the cello’s bass side is doing most of the resonating. As the frequency of the pitch that is ringing gets lower, the bottom half of the cello (bass side, don’t forget) takes over more and more of the resonating job. This is amazing to me, since the back side of the cello is made of only one material, maple wood, and so should be resonating at al the same frequency.

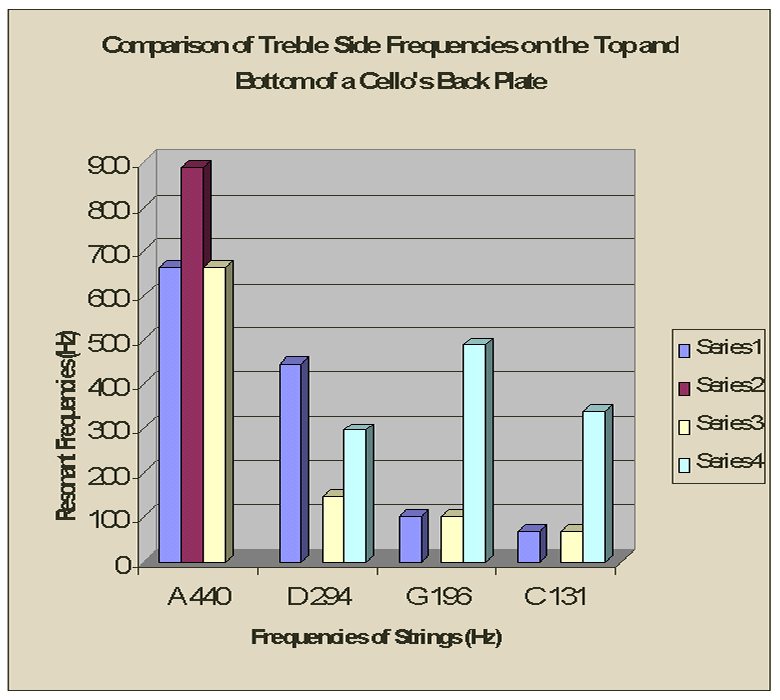
In the related graph unfortunately called "Comparison of Treble Side Frequencies on the Top and Bottom of a Cello’s Back Plate," an decreasing trend occurs in the first two Series of frequencies, or those that correspond to the part of the back diagonally opposite to the bottom half of the bass side (refer to figure below). This shows that the upper treble side resonates most prominently in the upper frequencies and gets less and less notable as the pitch of the string gets lower. By comparing this graph and the graph mentioned in the previous paragraph, one can deduce that the bottom bass quarter of the cello’s back side complements the top treble quarter of the back side in resonance. From this deduction, a skilled scientist could show that the cello does not have a resonating pattern such as the one seen in the twisting figure and on the violin below, because two opposite corners would be up and down.

In continuing this research, I would like to find out if there is any difference in timbre when different locations have certain resonances, or if it’s all the same so long as the resonance is balanced.

Note: The following page contains interesting examples of Chladni patterns on aluminum plates.
 
 

A Very Well-Done, Intriguing Luthier's Guide to Violin-Making
http://www.centrum.is/hansi/construction/
A Fantastic, Fascinating Look at Cymatics
http://www.alphaomega.se/english/cymatics.html
The Most Informative and Directly Related Site
http://www.phys.unsw.edu.au/~jw/chladni.html
Recipe for Your Very Own Stradivarius!
http://www.newscientist.com/ns/980404/nviolins.html
A Short Yet Provocative Piece About Sound Hole Sum Rule!
http://sound.media.mit.edu/~dpwe/AUDITORY/jasa/v77/n2/v77n2p710.html
Briefing on Modal Analysis of a Violin
http://sound.media.mit.edu/~dpwe/AUDITORY/jasa/v77/n2/v77n2p695.html
Comprehensive Page Over Violin Acoustics
http://www.phys.unsw.edu.au/music/violin/
It's All About Chladni Patterns, Baby!
http://keelynet.com/keely/chladni1.txt
Some Cool Chladni Patterns Which Oddly Resemble Those Seen Above...
http://www.regencynet.com/modal/chladni.htm