The Cartoon Water Tank Situation: Return to Research

Physics IA

Eric Blaettler

Tualatin High School

Word Count: 2052

Table of Contents

Introduction (Pg. 3-5)

Method (Pg. 6-7)
Materials (pg. 6)

Procedure (pg. 6-7)

Data (Pg. 8-14)

Raw Data (pg. 8-10)

Finding Flow Rate (pg. 10-13)

Graph Linearization(pg. 14)

Conclusion (Pg. 15)

Reflection (Pg. 16)

Bibliography (Pg. 17)

Related Websites (Pg. 18)

Introduction … Top

As a young kid something always fascinated me about cartoons. A leak would spring in a tank of water and water would gush out at high speeds, blasting away the character, and then the water would slowly trickle down into a slow dribble as the character walks back into the frame. I didn’t know how the water flowed out so fast, and I was unable to recreate this properly with a cup of water or a water bottle, so my question remained unanswered. In my physics class, I learned about Bernoulli’s principle which explained how a giant tank of water could have an initial rush of flow and then slow down as it drained more, it was its height. The equation made can also be modeled as its derivative, something else that heavily interests me as a math nerd.

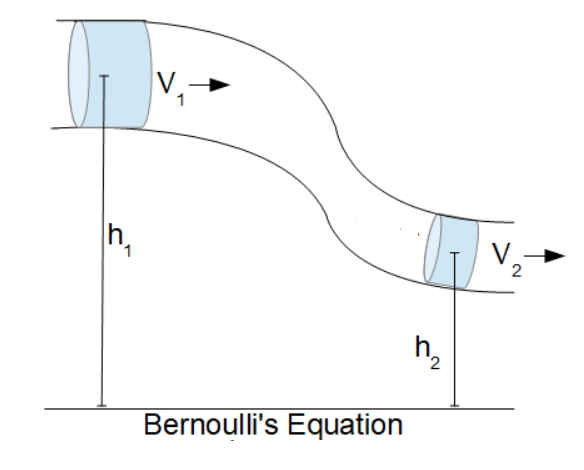
For this situation Bernoulli’s equation would be set up as ^[1], where v is the velocity of the water, p is the density of the water, g is the gravitational acceleration on earth(9.81)^[2], and h is the height from the top of the water to the drain hole. So as the water drains, the height of the water decreases and the velocity of the water going out decreases as well. Since the velocity at the top is much lower than the velocity of the water draining,  is nearly negligible in this equation^[3].

^[4]

Neglecting the velocity at the top can’t be used in all situations though, so this investigation will instead use the velocity at the top and the area of inside the bottle to get the most accurate calculation for flow rate.

This investigation will attempt to determine how the height of water in a container determines its flow rate by finding the relationship between the elapsed time and the height of the container. The independent variable is time and the dependent variable is the height of the water in the container. The controlled variables in this investigation are the temperature, density, and viscosity of the liquid, and the height and diameter of the container. I hypothesize that the container of liquid will have an initial rush of flow out and then slow down as it drains more over time due to the height of the water decreasing and reducing the potential energy. The rate at which water flows out of the container will decrease as the height decreases, and this decrease will begin gradually but will decay faster as the height further decreases. The equation for the flow rate is similar to the equation of whose graph has an initial growth rate that is high but then reduces as x increases. Since this investigation uses a decreasing independent variable, the flow rate will initially have a low decay rate, but as the height of the water decreases the flow rate of the water will decay more rapidly.

Graph of Derivative

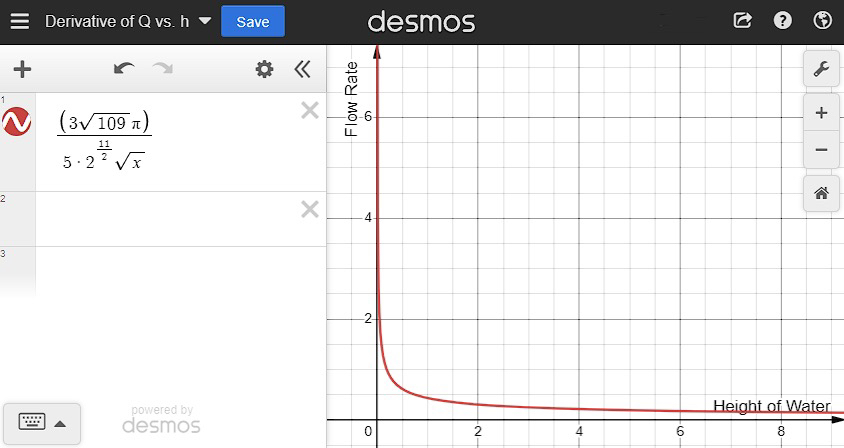
Graphing the derivative of the equation can further support my hypothesis. As can be seen with the graph of the derivative of , when the height is higher the change in flow rate is lower, but as the height gets low, the change in flow rate is much higher.

Method … Top

Materials

Materials for my investigation include a one liter Smartwater brand plastic water bottle, a metric ruler to establish a scale, dyed water to make video analysis easier, a phone with a stand to hold it parallel to the water bottle, and the Vernier Video Analysis program to simplify the process of collecting data from video. The bottle has a hole with a diameter of 0.5 centimeters that is 2 centimeters up from the base in order to avoid potential displacement from the indentation on the base. The indentation will likely not cause much interference, but it is best to avoid any unnecessary variables.

Procedure

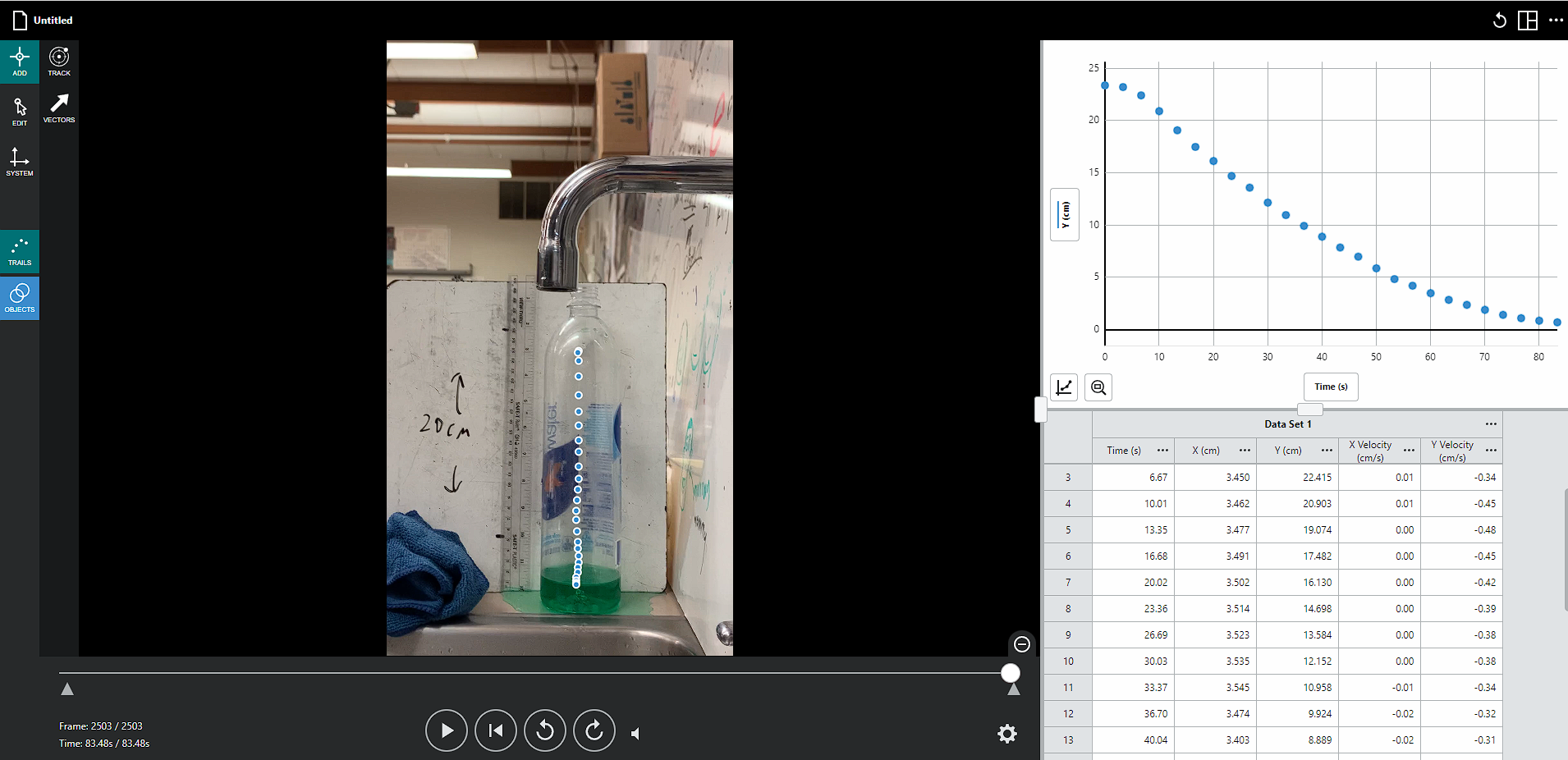
To conduct the experiment first I filled the water bottle up with water and then added dye in order for it to be more visible in the video. Due to the vacuum created, I was able to tighten the cap on the bottle to make the water not flow out of the hole. Then, unscrewed the cap of the bottle and recorded the water draining out until it started to slowly dribble out since the data collected after that wouldn’t be helpful in the investigation. Afterward, I downloaded my footage and put it into the Vernier Video Analysis program. This program allowed me to set a scale for the pixels in the video with reference to the ruler I put in the frame. From there I placed points of reference at every 100 frames which would create a total of around 25 frames of reference in the end. The Vernier Data Analysis program put all my data into a table which I could then move over into a spreadsheet which I could then use to graph my data. I then repeated this process two more times to have a total of three trials each with 24 to 31 points of variation. This variety of data points is due to the height of the water starting differently at each recording as well as human error during the video analysis section where I recorded points of data that wouldn’t be helpful for the investigation because they were so similar to the previous point. The results of three different trials could be averaged in order to neutralize the possible variation from the experiment, such as the starting height of the water. Doing around 25 different variations within the trials it would allow for a smooth graph in the end.

Example of Data Acquisition with the Vernier Data Analysis Program

Conducting this experiment does have the ethical concern of wasting water, so it is suggested that when repeating this experiment, collect and reuse the water for each trial. While my experiment only used around three liters of water in total, it is a good habit for any experiment where any resource can be reused instead of wasted.

The dependent variable of my experiment was the time elapsed and the independent variable was the height of water in the container. To measure the height of the water in the container I used the Vernier Video Analysis program in order to simplify the process, but noting the height of the water at second increments in a video would bring the same results, albeit more tedious. Variables that were controlled include the temperature, density, and viscosity of the liquid, the height and diameter of the container, the camera used, and the frame increment of the data collection. All of my experiments used room-temperature water from the same sink and four drops of food dye were added each time. This was all done to maintain the same density of the liquid in each trial. The same phone camera was used to record each trial in order to keep a consistent frame rate for the Vernier Video Analysis program so all the settings would remain constant and time increments would be the same.

Data … Top

Raw Data

Raw Data from Vernier Video Analysis
Trial 1		Trial 2		Trial 3
Time (s)	Y (cm)	Time (s)	Y (cm)	Time (s)	Y (cm)
0.0000	44.763	0.0000	34.049	0.0000	47.635
3.3350	43.336	3.3363	31.999	3.3356	45.751
6.6700	41.699	6.6725	30.585	6.6712	44.465
10.005	40.047	10.009	29.100	10.007	42.880
13.340	38.729	13.345	27.651	13.342	41.552
16.675	37.267	16.681	26.343	16.678	40.180
20.010	35.843	20.018	25.141	20.014	39.068
23.345	34.596	23.354	23.833	23.349	37.827
26.680	33.314	26.690	22.584	26.685	36.540
30.015	32.167	30.026	21.452	30.021	35.383
33.350	31.098	33.363	20.427	33.356	34.439
36.685	29.922	36.699	19.402	36.692	33.455
40.020	28.960	40.035	18.448	40.027	32.427
43.355	28.106	43.371	17.670	43.363	31.571
46.690	27.071	46.708	16.857	46.699	30.755
50.025	26.395	50.044	16.079	50.034	29.941
53.360	25.645	53.380	15.513	53.370	29.342
56.695	24.969	56.716	14.912	56.706	28.785
60.030	24.290	60.053	14.347	60.041	28.226
63.365	23.862	63.389	13.852	63.377	27.799
66.700	23.257	66.725	13.463	66.712	27.413
70.035	22.865	70.061	13.109	70.048	27.025
73.370	22.544	73.398	12.933	73.384	26.768
76.705	22.365	76.734	12.791	75.285	26.683
80.040	22.187	80.070	12.721
83.375	22.187	83.406	12.650
86.710	22.187	86.743	12.615
90.045	22.115	87.643	12.615
93.380	22.080
96.715	22.008
100.050	22.008

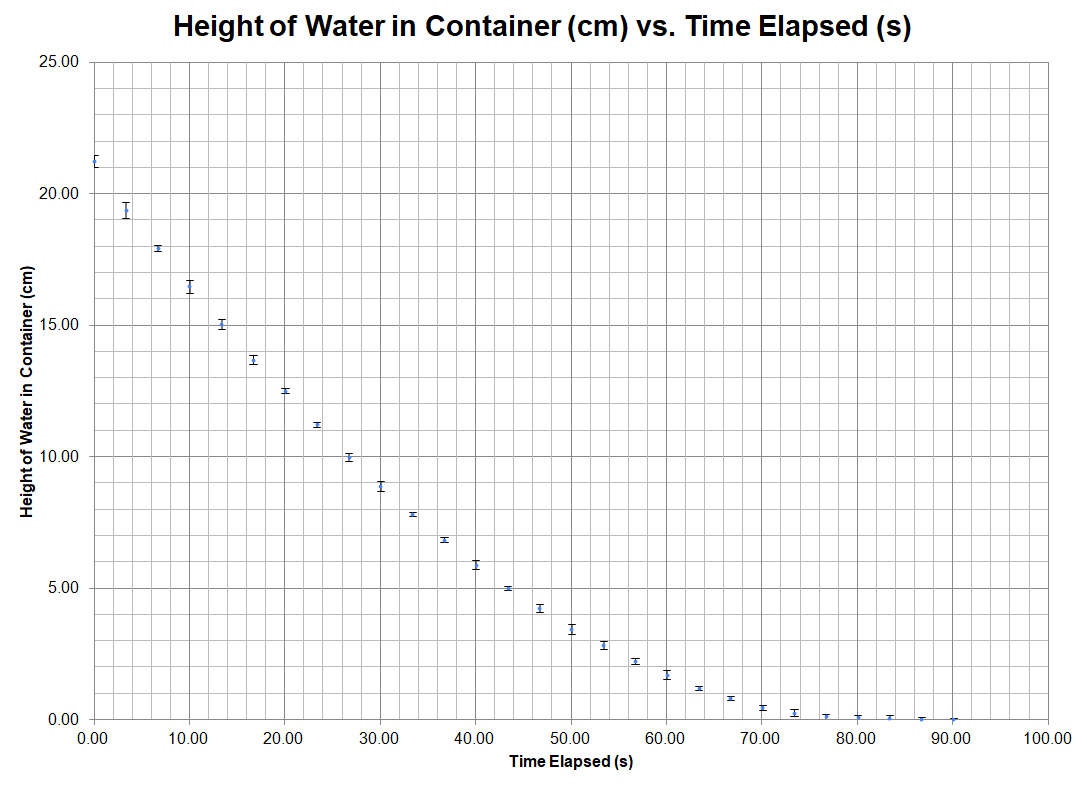
        Raw data is adjusted in order to have all trials start at similar heights, and to end with zero. The last frame was adjusted as well in order to fit into time increments of other trials and align with other trials. All trials are then averaged and uncertainties are found.

Time	Height of Water in Container
+/- .03	h / cm			cm	cm
x / seconds	Trial 1	Trial 2	Trial 3	Average	Uncertainty
0.00	21.33	21.43	20.95	21.24	0.48
3.33	19.69	19.38	19.07	19.38	0.62
6.67	18.04	17.97	17.78	17.93	0.26
10.00	16.72	16.49	16.20	16.47	0.52
13.34	15.26	15.04	14.87	15.05	0.39
16.67	13.84	13.73	13.50	13.69	0.34
20.01	12.59	12.53	12.39	12.50	0.20
23.34	11.31	11.22	11.14	11.22	0.16
26.68	10.16	9.97	9.86	9.99	0.30
30.01	9.09	8.84	8.70	8.88	0.39
33.35	7.91	7.81	7.76	7.83	0.16
36.68	6.95	6.79	6.77	6.84	0.18
40.02	6.10	5.83	5.74	5.89	0.35
43.35	5.06	5.05	4.89	5.00	0.18
46.69	4.39	4.24	4.07	4.23	0.31
50.02	3.64	3.46	3.26	3.45	0.38
53.36	2.96	2.90	2.66	2.84	0.30
56.69	2.28	2.30	2.10	2.23	0.20
60.03	1.85	1.73	1.54	1.71	0.31
63.36	1.25	1.24	1.12	1.20	0.13
66.70	0.86	0.85	0.73	0.81	0.13
70.03	0.54	0.49	0.34	0.46	0.19
73.37	0.36	0.32	0.09	0.25	0.27
76.70	0.18	0.18	0.00	0.12	0.18
80.04	0.18	0.11	0.00	0.09	0.18
83.37	0.18	0.03	0.00	0.07	0.18
86.71	0.11	0.00	0.00	0.04	0.11
90.04	0.07	0.00	0.00	0.02	0.07

Data file: text .:. Excel

Finding Flow Rate

To find the flow rate of water from the velocity of water inside the container, the displacement over time is found by finding the change in height and dividing it by the change over time. From there the velocity can be imputed in the equation . Q is the flow rate, and A is the area of the drain hole. In this table the velocity for the height of 21.24 cm. should be zero, but the bottle was already draining by the time the data was collected. In this situation, that height will be ignored.

Time	Averaged Water Height	Velocity Inside The Bottle	Flow Rate	Flow Rate Uncertainty
+/- .03
x / seconds	h / cm	v / cms^-1	Q / cm^3s^-1	Q / cm^3s^-1
0.00	21.24 +/- 0.24
3.33	19.38 +/- 0.31	0.56 +/- .01	21.46	0.31
6.67	17.93 +/- 0.13	0.43 =/- .00	16.71	0.05
10.00	16.47 +/- 0.26	0.44 =/- .00	16.90	0.08
13.34	15.05 +/- 0.20	0.42 =/- .00	16.29	0.05
16.67	13.69 +/- 0.17	0.41 =/- .00	15.81	0.04
20.01	12.50 +/- 0.10	0.36 =/- .00	13.68	0.02
23.34	11.22 +/- 0.08	0.38 =/- .00	14.76	0.01
26.68	9.99 +/- 0.15	0.37 =/- .00	14.14	0.02
30.01	8.88 +/- 0.20	0.34 =/- .00	12.93	0.03
33.35	7.83 +/- 0.08	0.31 =/- .00	12.08	0.01
36.68	6.84 +/- 0.09	0.30 =/- .00	11.45	0.01
40.02	5.89 +/- 0.18	0.28 =/- .00	10.89	0.02
43.35	5.00 +/- 0.09	0.27 =/- .00	10.28	0.01
46.69	4.23 +/- 0.16	0.23 =/- .00	8.85	0.02
50.02	3.45 +/- 0.19	0.23 =/- .00	9.02	0.03
53.36	2.84 +/- 0.15	0.18 =/- .00	7.08	0.02
56.69	2.23 +/- 0.10	0.18 =/- .00	7.08	0.02
60.03	1.71 +/- 0.16	0.15 =/- .00	5.96	0.03
63.36	1.20 +/- 0.07	0.15 =/- .00	5.88	0.02
66.70	0.81 +/- 0.06	0.12 =/- .00	4.48	0.02
70.03	0.46 +/- 0.10	0.11 =/- .00	4.09	0.04
73.37	0.25 +/- 0.14	0.06 =/- .00	2.35	0.05
76.70	0.12 +/- 0.09	0.04 =/- .00	1.56	0.05
80.04	0.09 +/- 0.09	0.01 =/- .00	0.27	0.01
83.37	0.07 +/- 0.09	0.01 =/- .00	0.27	0.01
86.71	0.04 +/- 0.05	0.01 =/- .00	0.41	0.02
90.04	0.02 +/- 0.04	0.00 =/- .00	0.14	0.01

At zero seconds the velocity cannot be found with the data collected because there exists no reference point before it to calculate displacement over time.

Diameter of bottle: 7 cm.^[5]

Since the uncertainty of area is a constant, all that needs to be done is to multiply the uncertainty of velocity by the area of the inside of the bottle.

v=.56 +/- 0.01 cms^-1.

A= cm.^2

0.01 *

Data file: text .:. Excel

Graph Linearization

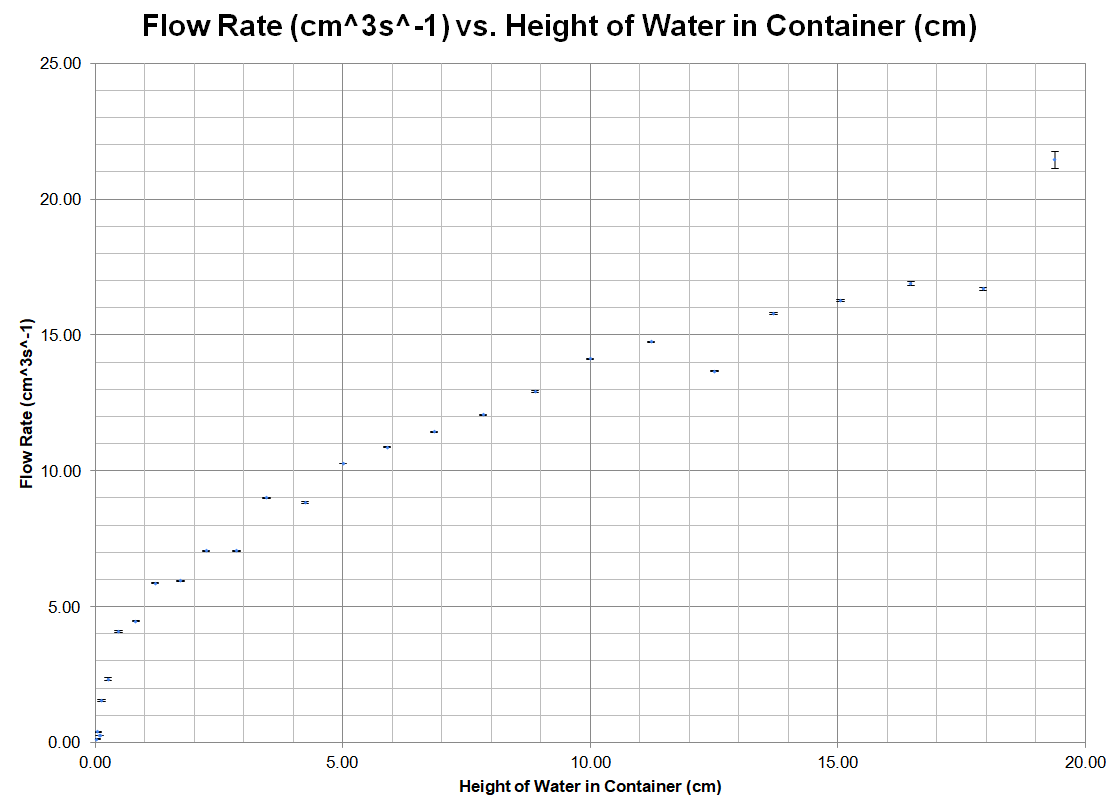
This is an attempt to linearize the data to understand the relationship between height and flow rate. In these graphs, x is the height of the water inside the bottle and y is the calculated flow rate.

)

Data file: text .:. Excel

Data file: text .:. Excel

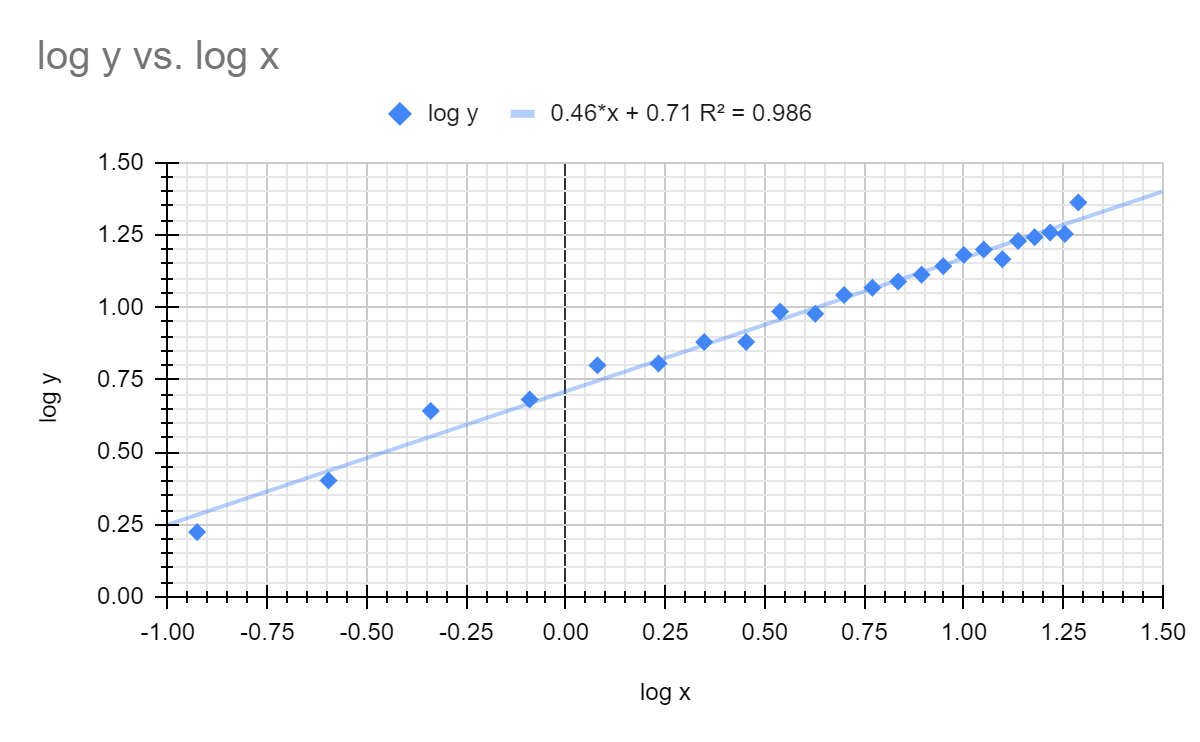
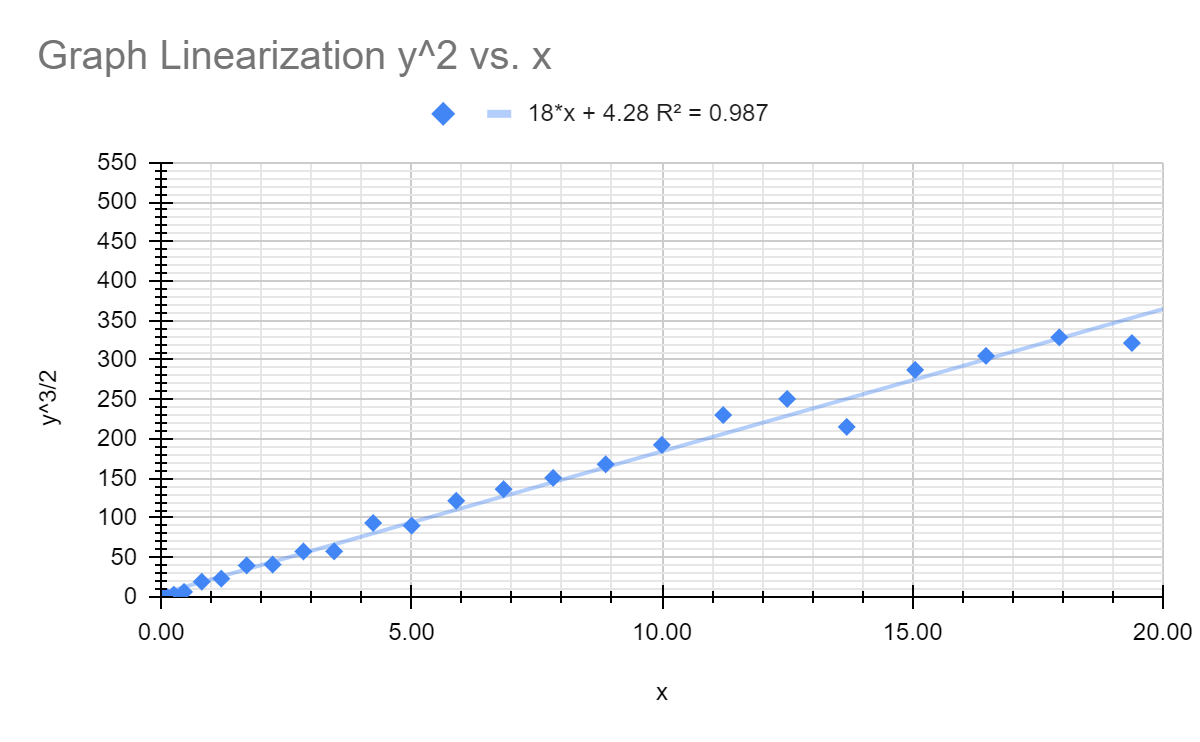
Conclusion … Top

        By looking at the data collected in the investigation, a conclusion can be drawn that supports my hypothesis. As seen in the graphs for flow rate, the flow rate decreases as the height decreases, and the decrease gets more intense as the height approaches zero. From 20 cm. to 5 cm. the line trends linearly, but once the height decreases past 5 cm. the slope rapidly increases. This change in slope is shown by a large decrease in flow rate.

        The reasoning behind the change in flow rate is best explained using conservation of energy and Bernoulli's equation. In this experiment, Bernoulli’s equation is set up as follows,

        As stated in the introduction, this equation can then be simplified by removing unneeded variables since the height of the out hole would be zero and the velocity inside the bottle is much smaller than the velocity out.

        What is left is a sequence of potential energy to kinetic energy. The potential energy being from the height of the water, and the resulting kinetic energy from the velocity the water drains out. As the water drains, the height will decrease, meaning that the potential energy in the sequence is lower, and kinetic energy will decrease as a result. Since velocity is the variable in the equation for flow rate, as the total energy in the sequence decreases, so will the flow rate.

 

Reflection… Top

        This investigation is limited in its methods for data collection. While the Vernier Video Analysis program gets rid of most of the human error when it comes to recording data, the water was turbulent throughout the experiment and didn’t provide a stable line to reference in the program. Most of this turbulence was caused by the unscrewing of the cap to the bottle to release the vacuum. While being able to tighten the cap and create a vacuum in which the water wouldn’t flow out of the drain hole was helpful for transporting the bottle from the sink to where the experiment was conducted, it resulted in turbulence with the water inside the bottle. To reduce turbulence as much as possible, it would’ve been better just to cover the drain hole until the water is still before beginning the trial. Additionally, this investigation could benefit from collecting the flow rate with a device in order to have data to compare with the flow rate calculation. I didn’t have access to the device needed to record this data, so all calculations had to be only theoretical. Even without this additional check, the calculations provide data which was to be expected with the investigation. Finally, Since all of the trials started at different heights, there exists a fair bit of uncertainty in this experiment. If I were to repeat this experiment I would measure each trial to the exact same amount in order to take away this uncertainty.

        If I wished to continue research on this topic I would investigate the variable of viscosity in this experiment. Making assumptions from the knowledge I have, the more viscous the fluid the slower it would flow out. Something I’m actually really curious about is the data collected from a liquid less viscous than water because I can’t picture how different the flow would be to water. The ethical concern of wasting resources would be more relevant with this change because many fluids are more expensive than water and could do damage to the pipes. Overall, adding this additional variable to the experiments interests me a lot and I’m likely to go forward with this research if I find myself with freetime.

Bibliography… Top

Smits, Alexander J. “Bernoulli's Equation.” Princeton University. The Trustees of Princeton University, February 5, 1997. https://www.princeton.edu/~asmits/Bicycle_web/Bernoulli.html.

Hathcox, Kyle, Glenn Marsch, and David Ward. “Physics.” Union University, January 2003. https://www.uu.edu/dept/physics/scienceguys/2003Jan.cfm.

University of Colorado Boulder, LearnChemE. “Draining a Cylindrical Tank.” YouTube. YouTube, June 4, 2012. https://www.youtube.com/watch?v=oIg2SxjF_Mg.

Khan, Sal. “What Is Volume Flow Rate? (Article) | Fluids.” Khan Academy. Khan Academy, 2015. https://www.khanacademy.org/science/physics/fluids/fluid-dynamics/a/what-is-volume-flow-rate.

McMahon, Arthur. “Smartwater Bottle Review: Water Bottle Review.” Backpackers.com, March 19, 2019. https://backpackers.com/outdoor-gear/reviews/smartwater-bottle-review/.

 

Related Websites… Top

        

https://demonstrations.wolfram.com/FlowFromATankAtConstantHeight/

Simuation of flow rate vs height. Cool little thing to observe and play with.

        

https://phys.libretexts.org/Bookshelves/College_Physics/Book%3A_College_Physics_1e_(OpenStax)/12%3A_Fluid_Dynamics_and_Its_Biological_and_Medical_Applications/12.01%3A_Flow_Rate_and_Its_Relation_to_Velocity#:~:text=Flow%20rate%20Q%20is%20defined,v%20is%20its%20average%20velocity

Good explanations of the equations relating to flow rate. I especially like diagrams that show the equations in action.

        

https://lambdageeks.com/does-height-affect-potential-energy/

Lots of random stuff here so mostly focus on just the potential energy stuff. Imagine the diagrams are showing water instead of balls.

        

https://www.youtube.com/watch?v=A3dQRhiTQdM

I don’t know what this video is trying to sell, but it shows that flow rate decreases as height decreases.

        

https://en.wikipedia.org/wiki/Bernoulli%27s_principle

Wikipedia page on Bernouli’s principle. Basically everything you need to know as far as equations go.