Finding the Sweet Spot

Sam Roach

Research Question: What is the relationship between where a ball strikes a baseball bat and its rebound percentage?

Background:

The baseball bat is one of the main instruments in “America’s Pastime”, the game of baseball. After playing baseball competitively for over 14 years, I’d call the sport a pastime of mine as well. Over the last few centuries, baseball bats have become increasingly efficient, and regulations have been changed for their dimensions and materials to safely fit the game. In the 1850s, baseball bats were all kinds of shapes and sizes. By 1969, the baseball bat had regulations such as a barrel no larger than 2.5 inches in diameter, and no longer than 42 inches in length. In 1884, the first Louisville Slugger was created out of white ash wood. Eventually, metal baseball bats were introduced to the game in the 1970s with the aluminum bat.

In an at bat where a batter faces a pitcher, if the batter makes contact, the baseball rebounds off of the bat to a certain extent depending on a few variables. The variables in play when a batter makes contact are the place where the ball hits, the material of the bat, swing speed, and the mass behind the swing. Aluminum bats generally have more rebound than a wood bat, and wood bats have different rebounding factors. Across all levels of baseball, bat regulations are constantly changing, looking for a balance between the entertainment and safety of the game. When the baseball makes contact with the bat, the biggest rebound occurs when there is minimal energy lost during contact. Every baseball player knows the feeling of making contact too close to the hands or too close to the end of the bat and shocking their hands. An explanation for this is when vibration is created during contact, energy is released and the ball does not travel as far. The estimated sweet spot of the bat where the energy lost to vibration is minimal is 17 cm from the end of the bat.

Statement of Problem:

The purpose of this experiment is to find the relationship between where a ball strikes a bat and the energy with which it rebounds. Rebound percentage will be measured by the height that the ball travels back up compared to the point at which it was dropped.

Variables:

The independent variable in the study is the width along the bat that the ball is dropped at. The dependent variable is the height that the ball rebounds in correspondence to the point it is dropped. The notable control variables are the drop height, and the materials of the bat and ball.

Hypothesis:

I think that the tennis ball will have the most rebound in between the end of the bat and the handle, and that the results will create a bell curve with steep edges.

Method/Procedure

Materials List:

-Tennis Ball

-Poster Board

-3 Clear Rulers

-Aluminum Baseball Bat

-Blue Tape

-File Cabinet

-Camera

Diagram

Procedure (Data collection):

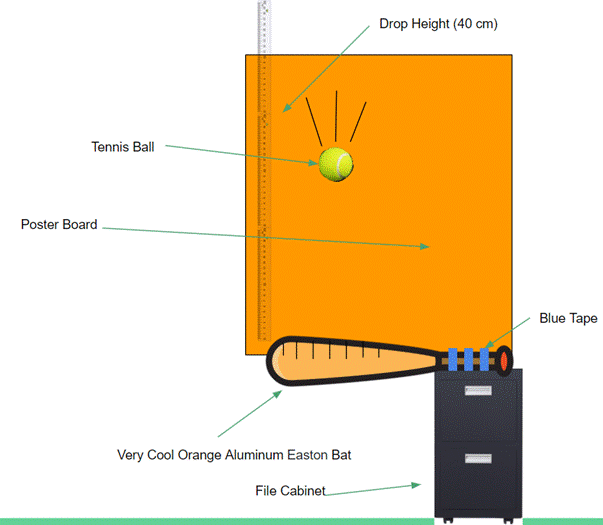
With all of the unique variables in the experiment, I decided to focus on certain ones that pertain to the rebound of the baseball without creating inconsistency. In collecting data, I started by clamping an aluminum bat between a vice, and dropping a lacrosse ball onto the bat at different points along the bat’s length. However, there was not much variation with the barrel being clamped between the vice, and the lacrosse ball made the barrel change elevation with every hit.

To make the experiment more convenient, I decided to tape the aluminum bat’s handle to a filing cabinet and switch the ball to a tennis ball. The tennis ball made sure that the tape did not tear from the force at contact.

The control variables were the baseball bat, rulers to measure height, the drop height of 40 cm, poster board in the back, the filming device, the tape, and the filing cabinet. The ball will be dropped the closest to the center as can be, and will be moved to different points on the length.

There were 10 locations with 3 trials at each drop spot, 3 cm apart that started 3 cm from the cap of the bat and moved towards the handle. Collecting 3 data points per spot allowed me to average the rebound height and percentage since hand dropping a bat onto a ball is not always exact. Having more trials per point allowed for more precision. With each trial, I dropped the tennis ball and made sure that the ball went directly up and did not ricochet to one side or the other. I simultaneously filmed the ball from the side and measured the percentage that the ball rebounded from its original drop point. The trickiest control variable to keep constant was the position of the bat because it sometimes moved when the ball was dropped, so I added more tape to the handle and weight to the filing cabinet. This way, the bat would not flinch with contact. When I got closer to the handle, the bat’s curvature made it bounce to the right, so I had to adjust the bat to continue gathering data.

Risk Assessment

In conducting this research, there are no significant risks. If the experiment were conducted with a lacrosse ball as intended, the ball could ricochet and hit something or someone. If this experiment is conducted with a lacrosse ball, make sure to pick an appropriate, controlled environment.

Data and Analysis

Table 1

	Rebound Height (cm)
Distance From End of Bat cm Δcm = ±0.5	Trial 1	Trial 2	Trial 3	Mean Rebound Height cm
3.0	22.0	22.0	21.5	21.8 ± 0.3
6.0	23.0	24.0	23.0	23.3 ± 0.5
9.0	23.0	24.0	24.0	23.7 ± 0.5
12.0	28.0	28.0	27.5	27.8 ± 0.3
15.0	27.0	28.5	30.0	28.5 ± 1.5
18.0	31.0	30.0	31.0	30.7 ± 1.5
21.0	30.0	29.0	29.0	29.3 ± 0.5
24.0	28.0	29.0	28.0	28.3 ± 0.5
27.0	26.0	25.0	25.0	25.3 ± 0.5
30.0	24.0	24.5	24.0	24.2 ± 0.3

Data File: Excel .:. Text

The uncertainty of the distance of contact from the end of the bat is ±0.5 cm because 0.5 is half the division of a centimeter and an appropriate uncertainty for dropping from 40 cm. There was also uncertainty in the rebound heights which stems from errors in dropping the ball. Examples: differing drop locations, tennis ball seams, drop velocity error, drop height error, rebound height measurement errors, etc… The uncertainty calculations take these errors into account.

Data Calculations:

The uncertainty of the mean rebound height in cm is calculated by taking the highest and lowest rebound heights at each respective distance and dividing them by 2. Take 3 cm from the end of the bat as an example.

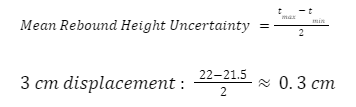
The uncertainty is rounded to 2 significant figures. This was done for all of the displacements.

The mean rebound height was calculated by adding all of the trials and dividing by 3. Here is the trial average of the first displacement of 3 cm as an example.

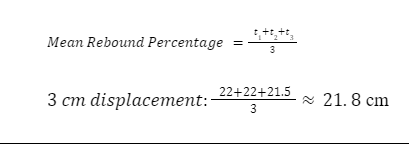
Table 2

	Rebound Percentage (%)
Distance From End of Bat cm Δcm = ±0.5	Trial 1	Trial 2	Trial 3	Mean Rebound Percentage
3.0	55.0	55.0	53.8	54.6 ± 0.6
6.0	57.5	60.0	57.5	58.3 ± 1.3
9.0	57.5	60.0	60.0	59.2 ± 1.3
12.0	70.0	70.0	68.8	69.6 ± 0.6
15.0	67.5	71.3	75.0	71.3 ± 3.8
18.0	77.5	75.0	77.5	76.7 ± 1.3
21.0	70.0	72.5	72.5	71.7 ± 1.3
24.0	70.0	72.5	70.0	70.8 ± 1.3
27.0	65.0	62.5	62.5	63.3 ± 1.3
30.0	60.0	61.3	60.0	60.4 ± 0.7

Data File: Excel .:. Text

Data Calculations:

The mean rebound percentage uncertainties were calculated by taking the highest and lowest trial numbers, finding their difference, and dividing them by 2. Take 3 cm from the end of the bat for example:

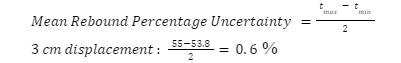
The uncertainty is rounded to 2 significant figures. This was done for all of the displacements.

The mean rebound percentage was calculated by adding all of the trials and dividing by 3. Here is the trial average of the first displacement of 3 cm as an example.

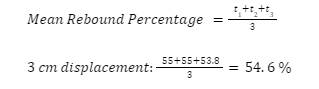
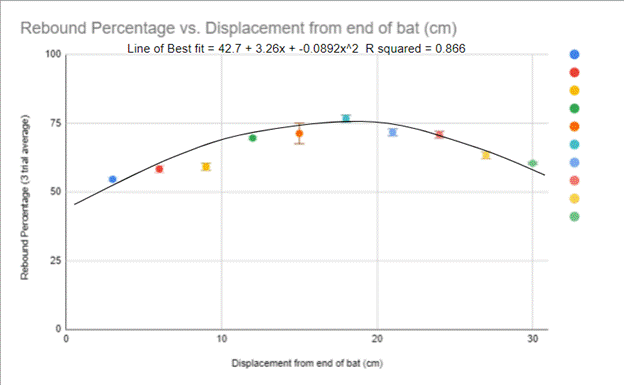
When placed on a graph, the data collected in the experiment shows that the closer that the ball gets to about 17 cm from the end of the bat, the higher the rebound percentage. Hence, there is more energy conserved at that spot. The displacement towards the respective edges of the graph represent the energy conserved when the ball makes contact with the end of the bat or handle. This energy lost must be the vibration felt whenever contact is made farther away from the sweet spot. The r squared value is 0.866 which means that there is moderately strong correlation between the data points. If the uncertainty of the points makes up for some of the drop error, the r squared value increases (at the places where the error bars come closest to the line of best fit). This means that the experiment could be even more accurate than observed.

In order to estimate the exact spot where rebound percentage is the highest, the maximum of the line of best fit must be found. To find that point, the derivative of the line of best fit will be taken and set equal to zero. The x intercept will reveal the point along the bat where the most energy is conserved at contact.

Derivative Calculations:

After taking the derivative of my line of best fit, the estimated sweet spot of the orange aluminum bat is 18.3 cm from the end of the barrel. External sources on the internet say that the sweet spot of a baseball bat is 10-18 cm from the end of the barrel (Russell).

Conclusion

The purpose of this experiment was to find the relationship between where a ball strikes a baseball bat and its rebound percentage. After compiling and analyzing the data, the original hypothesis matches the results. The relationship between rebound percentage and where a ball strikes a bat creates an upside down parabola, similar to a bell curve. Tables 1 and 2 show the correlation between rebound percentage/height and the point of contact along the bat. The maximum of that curve is where the ball had its greatest rebound percentage, and through the use of derivatives I was able to find the “sweet spot” of the bat at around 18.3 cm. Contrasting sources say that the sweet spot of a baseball bat is 10-18 cm from the end of the barrel which is very close to 18.3 cm. The maximum rebound point lies along the part of the bat with the thickest barrel radius. At the spots with the highest rebound percentage, there was less bat vibration observed at contact. Hence, the vibration observed most likely has to do with energy loss at contact.

Evaluation

Research Expansion:

One idea for further research would be sound wave analysis. If another study was conducted, I would use a microphone to analyze the sound waves created by energy loss in the bat.

Another avenue for further research is the correlation between the batter’s grip and where the sweet spot lies. When the bat did not have significant changes in rebound percentage when it was in a vice, it made me wonder what happens to the rebound percentage and sweet spot of the bat when it is held differently. To conduct this experiment, the bat could be put in circular clamps of different sizes or could be placed at different points along the bat, and the sweet spot could be calculated. However, doing this experiment would require ample amounts of research time and data. A team of researchers conducting and compiling similar studies to mine would be effective.

How climate affects rebound percentage is another idea for research expansion. In baseball, my team and I used to lay our bats in the sun to warm up the barrels for “more pop”. I wonder how the rebound percentage of the ball would change based on different climates. If I had extended time, I could do the experiment in different temperatures outdoors.

Strengths:

The experiment had a high r squared value, meaning that the data points had strong correlation to each other. They were not all over the place.

The bats sweet spot was where it was supposed to be according to other studies even with using a tennis ball. The experiment was accurate.

When the bat was successfully taped to the filing cabinet, there was no movement in the barrel during data collection. This allowed the experiment to have more precision.

Limitations and Improvements:

The ball was dropped with my hand, so there was always a possibility that my hand was not perfectly lined up with 40 cm. The r squared value showed that the data points were strongly correlated, but not exact. This could be due to the ball ricocheting ever so slightly to one side of the bat or the other. If I dropped the ball at a velocity of anything over or under zero, the rebound could be affected. To improve this, I could use a low friction material with holes in the side to allow me to drop the ball at the same velocity and elevation every time. This box would also allow the researcher to capture more trials at every spot since there would be less ricocheting.

The analysis of the ball with the camera was not exact. With the ball rebounding at different heights, there is surely a difference between the ball and the camera angle. To prevent this, I could use multiple cameras to capture multiple heights in which the ball rebounds to.

Since this experiment is mostly applicable to baseball, using a baseball would be more effective. However, a baseball has large seams, and it’s hard to drop in the same place every time. Dropping the ball from the box mentioned in scenario 1 would help.

The bat was placed on a narrow filing cabinet and made contact with almost all of the handle. In a realistic scenario, the bat would only be in contact with the batter’s hands. To give the experiment more external validity, the bat would have to be securely clamped around the handle in a similar manner to that of a batter’s hands.

Links

https://link.springer.com/book/10.1007/978-1-4419-8113-4 While reviewing the physics of contact with bat and ball. They also discuss probability when it comes to making contact with the ball in the batters box.

https://www.acs.psu.edu/drussell/bats/sweetspot.html. The website says that the sweet spot is 5-7 inches from the end of the barrel which correlates directly to what mine is. The website also talks about the center of percussion.

http://baseball.physics.illinois.edu/ball-bat.html. The website discusses how the bat is a free object; therefore, grip does not matter. Feats that look like strength oftentimes have nothing to do with the strength of the batter since the bat is a free object.

https://www.baseballbats.net/about-bats/the-evolution-of-bats/. The rebound of aluminum bats compared to wood is discussed. This is relevant to my research because I deal with an aluminum bat.

https://www.real-world-physics-problems.com/physics-of-hitting-a-baseball.html

The sweet spot of the bat is where maximum energy is transferred and minimal amounts are lost. Certain vibration sends the ball to greater lengths.

Bibliography

Cross, Rodney. Physics of Baseball & Softball. Springer, 2011.

“The Evolution of Baseball Bats.” BaseballBats.net, https://www.baseballbats.net/about-bats/the-evolution-of-bats/.

Nathan, Alan M. The Physics of Baseball, University of Illinois, http://baseball.physics.illinois.edu/ball-bat.html.

Russell, Daniel A. “The Sweetspot of a Hollow Baseball or Softball Bat.” What(and Where) Is the Sweet Spot of a Baseball/Softball Bat?, 27 Mar. 2008, https://www.acs.psu.edu/drussell/bats/sweetspot.html.