What effect does changing
the length of a pendulum string have on the period of a simple pendulum?
Hannah
Figueroa Velazquez
Introduction
and Background | Hypothesis | Materials | Method | Risk Assessment | Data and Analysis |
Conclusion | Evaluation
| Limitations | Further
Research Suggestions | Bibliography | Related Websites | Return to
research
Back and forth, back and forth. The consistent motion of a pendulum seemed like magic to me as a child, and it wasn’t until I joined physics in high school that I began to understand the mathematics and science behind such a mystical object. Was it the bob at the end that moved it forward or was this a simple gravity problem? Through more research, I was able to identify the various factors that impacted the motion of a pendulum, one of them being simple yet fascinating: the length of a pendulum string.
The simple pendulum, a perfect example of Newton's first law of motion[1]: the law of inertia, faces downwards at a 90 degree angle as it’s pulled down by gravity at rest.[2] When a force is applied on it, however, the object receives inertia and must stay in motion until forcibly stopped. The structure consists of a mass or “bob” hanging from a string which is attached to a pivot point that allows for the bob to be swung at any angle. Though not exact, the motion of a pendulum with small angles resembles that of simple harmonic motion which results when a restoring force is proportional to the displacement.[3] The angular displacement is the angle of which the pendulum has been drawn back before released and for this reason when displacement is zero, this position is known as the equilibrium position as seen in figure 1.
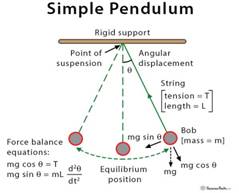Figure 1[4]
Furthermore, the pendulum has been of interest to physicists dating back to 1583 when Italian mathematician and astronomer, Galileo, discovered the relationship between a swinging lamp and his pulse rate.[5] The time in which the lamp took to complete a full swing remained perfectly constant, a tool that the scientist saw could be used for precise timing. In other words, he discovered the “period” of the lamp. A period in physics refers to the time it takes to do one complete cycle. While in waves this means the amount of time it takes for a particle to make a complete vibrational cycle, in a pendulum this means the amount of time it takes to complete a full swing. When noted that the pendulum was affected by length of string and independent of its amplitude, Galileo began imagining uses for the constant oscillation of a pendulum swing such as music tempo for students, taking a pulse, and for improving the accuracy of clocks as seen in the development of grandfather clocks.[6] He wanted to conclude what factors exactly changed the period and timing of a pendulum model.
Finally, it was determined that the mass of a bob at the end of a pendulum had no impact on the period as the gravitational acceleration of which the pendulum was being pulled remained constant regardless of mass added. Likewise, the angular displacement of the pendulum had no influence on period as the greater the angle, though it’s covering a greater space, there’s also a greater amount of acceleration occurring.[7]. On the other hand, changing the length of the pendulum string as Galileo witnessed altered the amount of time it took for the pendulum to complete a full swing.
The purpose of this investigation is to determine the effect a length of a pendulum string has on the period of a simple pendulum. My independent variable is the length of the string and my dependent variable is the period of the oscillation in seconds. My controls are the mass of the bob on the pendulum and the angle at which the bob is dropped.
I believe that as the length of the pendulum string increases, the period will also increase in a linear manner as longer strings will make for longer times taken to complete a full swing just as shorter strings will produce more rapid movement meaning that length and time are directly proportional.
In this experiment I used a pendulum stand that my physics teacher had available in his classroom which I set on a table so that I was able to manipulate my lengths more freely. I also used a long string which I attached to a metal weight and tied to the top of the pendulum stand at different heights depending on what length I wanted. I used a metal clamp to provide more security and ensure that the string wouldn’t slip. The height of the pendulum stand was approximately 120 cm with an estimated uncertainty of about .05 cm. The metal weight at the bottom of the string was 170 grams with an uncertainty of .05 grams. I used a meter stick to measure all of my string lengths and finally I attached a protractor with tape to the top of my pendulum stand and made sure the 90 degree mark aligned with my string when it was at equilibrium as seen in the diagram below.
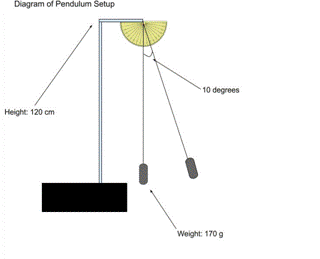Figure 2
First, I measured the length of the string needed for my first string length and marked that point with a sharpie on the string of the pendulum. I used lengths ranging from 10.2 centimeters to 82.6 centimeters increasing each time by increments of 3.8 centimeters so that my data would be consistent. Then, I tied the string on the top of the pendulum stand at the point where the sharpie mark had been drawn using a clamp to ensure that my string would stay in place and movement wouldn’t interfere with my result.. Afterward, I grabbed the pendulum weight and drew it out from equilibrium until the string aligns with the 10 degree mark on the protractor attached to the top of the pendulum stand. As soon as the string was aligned with the 10 degree mark, I released the weight at the same time I began recording on a stopwatch the time it takes for the string to make 10 full back and forth swings. Finally, I ended the stopwatch as soon as the pendulum had finished it’s 10th full oscillation and recorded the time. I did 3 trials for each string length and 20 variations of string length total so that I had enough data points to get a clear image of the correlation between string length and period of an oscillator.
There’s no risk involved in this experiment as long as the pendulum weight is tightly secured to the string nobody is standing in the swing area of the pendulum. There’s no environmental harm done by partaking in this investigation.
Data Table 1: Raw data displaying 3 trials for 20 different length variations
|
Length of Pendulum String ± .05 cm |
Time For 10 Full Oscillations ± .05 s |
||
|
Trial 1 |
Trial 2 |
Trial 3 |
|
|
10.2 |
6.29 |
6.40 |
6.55 |
|
14.0 |
7.56 |
7.45 |
7.23 |
|
17.8 |
8.32 |
8.65 |
8.43 |
|
21.6 |
9.61 |
9.72 |
9.84 |
|
25.4 |
10.31 |
10.15 |
10.01 |
|
29.2 |
11.20 |
10.90 |
10.76 |
|
33.0 |
11.83 |
11.56 |
11.29 |
|
36.8 |
12.36 |
12.19 |
11.98 |
|
40.6 |
13.50 |
13.35 |
13.23 |
|
44.5 |
14.12 |
13.89 |
13.74 |
|
48.3 |
14.57 |
14.31 |
14.27 |
|
52.1 |
15.11 |
15.09 |
14.67 |
|
55.9 |
14.99 |
15.12 |
15.21 |
|
59.7 |
15.75 |
15.53 |
15.31 |
|
63.5 |
16.22 |
16.01 |
15.83 |
|
67.3 |
16.24 |
16.77 |
16.52 |
|
71.1 |
17.02 |
17.28 |
17.46 |
|
74.9 |
17.91 |
17.77 |
17.57 |
|
78.7 |
18.02 |
18.21 |
17.76 |
|
82.6 |
18.29 |
18.75 |
18.55 |
|
Mass of Pendulum Weight: 170 ± .5 g |
|||
|
Height of Pendulum: 120 ± .05 cm |
|||
Data table 1 displays my raw data after 20 different string lengths with 3 trials each. I calculated that because I used a meter stick with increments of .1 centimeters, an uncertainty of .05 centimeters was reasonable which is the same logic I used for my .05 uncertainty for the height of my pendulum. As for my time, I was measuring to the .01 second which is why I chose to assume an uncertainty of .05 seconds. Finally, for my pendulum weight I was measuring its weight in grams which is why I used an uncertainty of .5 g.
Data Table 2: Converting the raw data into averages and calculating the uncertainty
|
Length of Pendulum String ± .05 cm |
Calculating The Time For 1 Full Oscillation ± .05 s |
|||||
|
Trial 1 |
Trial 2 |
Trial 3 |
Average |
Average/10 Swings |
Uncertainty |
|
|
10.2 |
6.29 |
6.40 |
6.55 |
6.41 |
0.641 |
0.013 |
|
14.0 |
7.56 |
7.45 |
7.23 |
7.41 |
0.741 |
0.017 |
|
17.8 |
8.32 |
8.65 |
8.43 |
8.47 |
0.847 |
0.017 |
|
21.6 |
9.61 |
9.72 |
9.84 |
9.72 |
0.972 |
0.012 |
|
25.4 |
10.31 |
10.15 |
10.01 |
10.16 |
1.016 |
0.015 |
|
29.2 |
11.20 |
10.90 |
10.76 |
10.95 |
1.095 |
0.022 |
|
33.0 |
11.83 |
11.56 |
11.29 |
11.56 |
1.156 |
0.027 |
|
36.8 |
12.36 |
12.19 |
11.98 |
12.18 |
1.218 |
0.019 |
|
40.6 |
13.50 |
13.35 |
13.23 |
13.36 |
1.336 |
0.014 |
|
44.5 |
14.12 |
13.89 |
13.74 |
13.92 |
1.392 |
0.019 |
|
48.3 |
14.57 |
14.31 |
14.27 |
14.38 |
1.438 |
0.015 |
|
52.1 |
15.11 |
15.09 |
14.67 |
14.96 |
1.496 |
0.022 |
|
55.9 |
14.99 |
15.12 |
15.21 |
15.11 |
1.511 |
0.011 |
|
59.7 |
15.75 |
15.53 |
15.31 |
15.53 |
1.553 |
0.022 |
|
63.5 |
16.22 |
16.01 |
15.83 |
16.02 |
1.602 |
0.019 |
|
67.3 |
16.24 |
16.77 |
16.52 |
16.51 |
1.651 |
0.027 |
|
71.1 |
17.02 |
17.28 |
17.46 |
17.25 |
1.725 |
0.022 |
|
74.9 |
17.91 |
17.77 |
17.57 |
17.75 |
1.775 |
0.017 |
|
78.7 |
18.02 |
18.21 |
17.76 |
18.00 |
1.800 |
0.023 |
|
82.6 |
18.29 |
18.75 |
18.55 |
18.53 |
1.853 |
0.023 |
|
Mass of Pendulum Weight: 170 ± .5 g |
||||||
|
Height of Pendulum: 120 ± .05 cm |
||||||
Data table 2 shows the process I used for converting my trials into averages, turning time for 10 swings into 1, as well as measuring individual uncertainties for each one of averages. Taking the averages for each string length was simple as I just had to add up the quantities of the 3 trials and divide by 3 to get my average. For instance, for my string length of 10.2 centimeters, my calculation looked like this:
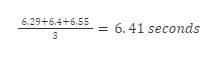
Next, I divided each of my estimated uncertainties by 10 since I calculated the time needed for the pendulum to make 10 full swings while period only refers to 1. Once I had my average periods calculated, I went through and calculated individual uncertainties which I calculated by subtracting the smallest trial value for a given string length from the highest trial value and dividing that number by 2. An example of the calculation looked like:
seconds
Now that I had calculated my averages and uncertainties, I was able to compile all my data into a power function graph as shown below.
*My error bars were too small to be displayed in my graphs
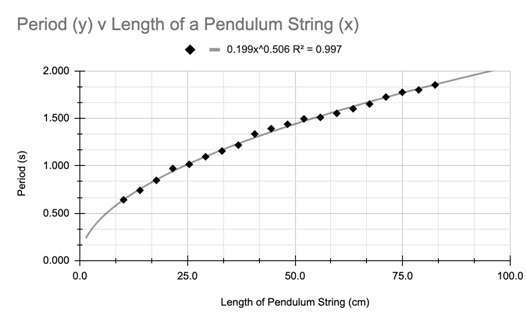
From this graph I was quickly able to see that contrary to my hypothesis, although length of string does have an effect on the period of my pendulum, the two variables form a power function, not a linear one as I had predicted. The time period of the simple pendulum is directly proportional to the square root of its length, meaning that if I were to double the length of the string then the period would increase as well but not by exactly double. I can derive from the strong correlation and the exponent of .5, that the period is roughly equal to the square root of the length with a constant being multiplied in front. I can analyze this relationship further by linearizing my data.
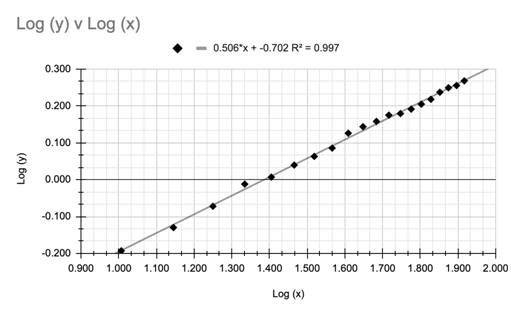
Because
I learned that my data could be shown as a power function, I decided to linearize it by graphing the log of my Y values against the
log of my X values which resulted in a linear graph. I can use the resulting
equation to deduce the value of the coefficient A, and the power n since I know that power
functions are represented by 
where n will be the slope of my line. Since my slope value is about
.5, I can determine that to linearize my graph I will
need to raise my Y value to the 
power, which in this case would be 
or
2.
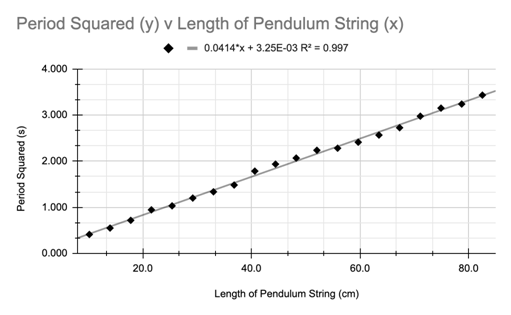
Finally,
once I deduced that I needed to square my Y values in order to linearize my data, I was given a linear trendline
that proved the square root relationship of length and period. Some aspects of
the graph are a product of human error such as the y-intercept being 3.25E -03
implying that when the length of the pendulum string is 0, the period is not.
This answer is nonsensical but certainly the intercept is close enough to 0 so
that my data still remains significantly accurate and representative of the
relationship. This discovery led me to wonder what were the
physics behind this square root correlation between length of a pendulum
string, and its period.
I
investigated deeper into simple harmonic motion and found a widely accepted
equation for the period of a simple pendulum that only worked with small
angles. With the use of geometry and different equations, I was able to derive
this formula and better understand the nature of my findings.
Figure
3
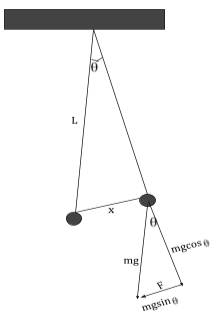
In
this diagram we can begin to understand the correlation between length and
period of a simple pendulum as L is the length of the pendulum swing and 
is the among of degrees by which the string was pulled from
equilibrium. Thanks to small angle approximation, though the triangle created
by the pendulum swing isn’t exactly a right angle, the
angle is small enough that we assume either side could be the hypotenuse. mg is the force acting downwards on the mass which helps us
to understand using trigonometry that the horizontal vector of force acting
upon the mass (F) is equal to mgsin. We can calculate this since we know that:
So in this case, the equation would
look like:
By
moving this around with algebra we can conclude that the horizontal force
vector is equal to mgsin. Furthemore, we can use the triangle created by
the pendulum to compare what sin equals in terms of l
and x. Once again by using trigonometric rules we can identify x as opposite to
and l as the hypotenuse.
This leads us to the equation:
Through the use of
substitution we can rewrite the horizontal force vector acting on the mass to
be:
Now, we can derive the
general formula for period (T) by using the formula for angular velocity (w)
given by:
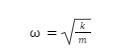
which applies for small displacements as the one used in my
experiment. Next I can use the equation:
to help me substitute 
in for w which by multiplying 
by the reciprocal of 
, I get the general of equation for period given by:
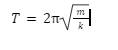
Finally, I can use Hooke’s Law which identifies that as long
as angle of displacement is small, the restoring force of the displaced mass follows
simple harmonic motion which is given by the formula of:
Clearly, we can see how this resembles our derived formula
of:
where k in this case is equal to 
Now that we’ve identified what k is equal to, we can once
more use substitution to sub in 
for k in the equation 
This leaves us with the equation:
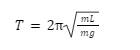
where the mass conveniently cancels out and leaves us with
our final equation for period of a pendulum:
Now that we have our derived formula, we can determine how
accurate our results were and what disparities were caused by factors such as
human error as well as external forces such as air friction. By moving around
the formula, we get that the period in seconds is equal to a constant
multiplied by 
where the constant is 
. If we use 981 
as our value for gravity,
then this constant would be roughly equal to .2006. Comparing this to the value
we got in our first graph’s equation which depicts period v length of pendulum
string, you can see that the square root of length is being multiplied by a
constant of .1990 which is extremely close to the constant in our derived
formula with only a .0016 value difference. Likewise, once our graph has been
linearized we are presented with the a slope that tells us the constant being
multiplied by LA in order to get the period squared
which by moving around our original equation would give us a constant of 
. By calculating this you
get approximately .04024. When compared to the slope we got which was a value
of .0414, you see that once again though slightly skewed due to error the
values are strikingly similar with a difference of only .00116. Finally, we can
attribute some of the calculated error to the slight disparity in value that
comes with using the small angle approximation which states that when 
is small enough, the
sin of approximately equal
to . Looking back at our
general equation for period, we see that:
which we can rewrite to display:
By moving this equation around algebraically we are left
with:
Since I used an angle of 10 degrees in my investigation, that
means that if I convert 10 degrees to radians I am given .1745 radians. Sin of
.1745 radians is approximately .1736. This means that we can rewrite our
formula to look like:
By simplifying the equation we are left with:
Meaning that the period calculated will be about .26% too high
by using the small angle approximation. Of course, most of the error can be put
upon human error as there were various aspects of uncertainty throughout the
investigation.
Ultimately, the square root correlation is no coincidence,
and you can see how the underlying reason is because the time taken to make a
full swing is dependent on the value of the restoring force, or the mgsin
, which in the case of
small angles, we can substitute the degree for 
, meaning angle of
displacement has virtually no effect on the period while length does. In the
same way, because we can end up canceling our mass in our equation, the mass of
the pendulum weight doesn’t impact the period either. The smaller length is,
the greater the restoring force and therefore, the time taken to complete a
full oscillation is less.
Finally, my results confirmed parts of my hypothesis and
rejected others. I imagined that as the length of the string increased, the
period would increase as well, but I wrongly predicted that the relationship
would be directly proportional and result in a linear graph. Rather, I found
through graphing my data and deriving the formula for the period of a simple
pendulum, that the period of a function is equal to the square root of length
multiplied by a constant. As you increase the length of the pendulum string,
you’re decreasing the amount of restoring force as the horizontal gravitational
component will have a less steep slope downward resulting in less of a force.
Though my data was extremely similar to what one would expect
given the established formula for the period of a function, there were several
sources of human error that, if fixed, could provide more accurate results.
Much of the error has to do with the design, as I was timing the amount taken
for 10 complete oscillations with the human eye, and much of the uncertainty
was due to me not being able to precisely end my stopwatch exactly at the time
that the 10 swings ended. One solution for this would be to let the pendulum
swing for more than 10 swings, as it would give a clearer result, but even this
wouldn’t completely solve the issue of the human eye not being fast enough to
clearly tell when the pendulum has reached its last oscillation. If I were to
redo this experiment, I’d use technology to make my results more accurate. If I
were to videotape the pendulum on a video analysis app I would be able to
perfect my timings and have less margin of error in my times. I could even use
slow motion features to tell when exactly the oscillation ended.
Additionally, another source of potential error was with
measuring the length of my pendulum strings. Although I measured the string
each time as accurately as I could, I wasn’t able to perfectly account for the
amount of string that would be used to tie the string on the pendulum stand. If
I were to change this, I would, instead of tying the string, use a stronger
clamp that would be able to hold the weight of the pendulum which would
therefore mitigate the amount of string being tied around the metal rod.
Finally, one of my greatest sources of error in the
experiment would be how I struggled to accurately time and calculate the time
taken for 10 complete swings as the length got increasingly shorter. I quickly
noticed that although 10 degrees was a good angle for long string length, such
a small displacement from equilibrium for small string lengths made the movement
too rapid and shaky to properly measure. Though it’s crucial that the angle
remain small in order to be able to use small angle approximation, I think for
future experiments I would start my string lengths out greater so that my range
would start at a greater value and I wouldn’t have to rely on inaccurate
results for my first few data points.
As I was fascinated by the results of my experiment, I’d be
curious to investigate less widely researched aspects of the simple pendulum.
For instance, as I was researching I found that though there hasn't been much
research done on the subject, it’s been proven that diameter of the string can
actually impact how quickly the pendulum’s oscillations dampen. In the future
I’d be interested to learn more about what affects dampening in a simple
pendulum and how we can manipulate the speed of dampening by changing the
strings being used.
Admin. “Simple Pendulum Derivation
of Expression for Its Time Period - w3schools.” W3spoint, 29 Feb. 2020, https://www.w3schools.blog/simple-pendulum-derivation-of-expression-for-its-time-period.
Buddies, Science.
“Swinging with a Pendulum.” Scientific American, Scientific American, 23 Feb.
2012, https://www.scientificamerican.com/article/bring-science-home-swinging-pendulum/.
“The Galileo Project:
Science: Pendulum Clock.” The Galileo Project | Science | Pendulum Clock, http://galileo.rice.edu/sci/instruments/pendulum.html.
“Gary Garber's Blog.” Gary
Garbers Blog SHM in a Pendulum Comments, http://blogs.bu.edu/ggarber/interlace/pendulum/shm-in-a-pendulum/#:~:text=The%20motion%20of%20a%20simple,Law%20when%20applied%20to%20springs.&text=Where%20F%20is%20the%20restoring,and%20x%20is%20the%20displacement.
“Newton's Laws of Motion.”
Encyclopædia Britannica, Encyclopædia Britannica, Inc., https://www.britannica.com/science/Newtons-laws-of-motion.
Oscillations - University
of Michigan. http://www-personal.umd.umich.edu/~jameshet/IntroLabs/IntroLabDocuments/150-11%20Oscillations[2]/Oscillations[2]%205.0.pdf.
Perdue, Matthew. “The
Factors That Might Affect the Period of Oscillation.” Sciencing, 13 Dec. 2020, https://sciencing.com/factors-might-affect-period-oscillation-8437461.html.
Reinbold, Joan. “Why Does
a Pendulum Swing?” Sciencing, 2 Mar. 2019, https://sciencing.com/pendulum-swing-5280650.html.
“Swinging on a String -
Lesson.” TeachEngineering.org, 22 Feb. 2022, https://www.teachengineering.org/lessons/view/cub_mechanics_lesson09.
\
https://www.acs.psu.edu/drussell/Demos/Pendulum/Pendulum.html
This site is helpful in explaining the derivation of the
formula for period of a simple pendulum as well as displays diagrams that allow
for one to see the forces acting on the bob as it swings.
http://hyperphysics.phy-astr.gsu.edu/hbase/pend.html
This site allows for you to insert length of string and
therefore calculates period for you. Your data should be a little different but
similar meaning this is a good site to check that you’re on the right track.
https://file.scirp.org/Html/7-1720775_73856.htm
This site explores a different but similar aspect which is
the effect of mass on string on damping of a simple pendulum. It’s more
advanced but a good potential project for research.
This site is useful because it explains simple harmonic
motion which is necessary for your introduction and background if you’re doing
anything related to pendulums.
https://www.khanacademy.org/science/physics/mechanical-waves-and-sound/harmonic-motion/v/pendulum
This is a video that I watched to get a better understand
of SHM and how to draw my diagrams when explainingf the forces acting on the
pendulum.
[1] https://www.britannica.com/science/Newtons-laws-of-motion
[2] https://sciencing.com/pendulum-swing-5280650.html
[3]http://blogs.bu.edu/ggarber/interlace/pendulum/shm-in-a-pendulum/#:~:text=The%20motion%20of%20a%20simple,Law%20when%20applied%20to%20springs.&text=Where%20F%20is%20the%20restoring,and%20x%20is%20the%20displacement
[4] https://www.sciencefacts.net/simple-pendulum.html
[5] https://www.teachengineering.org/lessons/view/cub_mechanics_lesson09
[6] http://galileo.rice.edu/sci/instruments/pendulum.html
[7] https://sciencing.com/factors-might-affect-period-oscillation-8437461.html