By Dmitriy Shepelev

Background: .:. Top

Nearly everyone has faced a situation in which a container filled with liquid is discovered to be leaky. Although a major inconvenience, it is also a source of scientific inquiry for me. Given a constant gravitational force of -9.81N, there are many factors that may affect the time it takes for a liquid to issue completely from a container. In this investigation, I will analyze the relationship between the diameter of a hole in a container, measured in inches, and the time, measured in seconds, it takes for the liquid to leak completely from the container.

Statement of Problem: .:. Top

The purpose of this investigation is to measure how changes in the diameter of a punctured hole affect the time it takes for water to issue completely from a water bottle.

Hypothesis: .:. Top

Given a constant gravitational force of -9.81N, I believe that as the diameter of the water hole increases, the time for the water to issue will decrease.

Materials: .:. Top

· Electric drill.

· Screws ranging from 9/64’ to 16/64’.

· Empty 591ml water bottle.

· Facet with running water.

· Timer on phone.

Procedure:

Create a small air hole (7/64’) at the bottom of the water bottle in order to increase air pressure in the water bottle. This will cause the water to issue from the water bottle. Drill a hole of diameter 9/64’ in the cap of the water bottle. Fill water bottle to the top, making sure that no water leaks through the air hole. Put the cap onto the water bottle. Flip the water bottle, with the cap pointing downward, and time how long it takes for all of the water to issue from the bottle. Conduct three trials. Then, increase the diameter of the water hole by 1/64’ with an electric drill and conduct three trials again. Repeat this until the diameter of the water hole is at a size of 16/64’.

Data: Excel .:. Text .:. Top

Given that time, measured in seconds, is the dependent variable, and the diameter of the water hole, measured in inches, is the independent variable, the following models the relationship between time (s) and diameter (in):

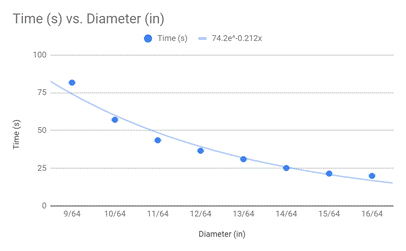
Chart

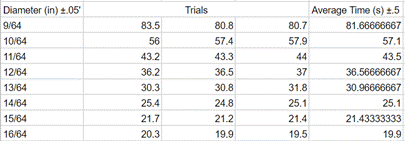
Discussion and Sources of Error: .:. Top

Evidently, the data points appear to follow an exponential decay function. This means that my hypothesis is correct, that as the diameter increases, the time it takes for water to issue from a water bottle decreases. In order to model this relationship, I generated an equation via Google Sheets: 74.2e^-0.212x. A closer look at the data reveals that most points are fairly close to the equation, except the first data point. Looking at the first row of the trials, the first time of 83.5 seconds seems to have skewed the average time, since the latter two trials are at 80.8 and 80.7 seconds.

There are many possible sources of error within this investigation that, if rectified, would improve this investigation. For example, one source of error is the fact that throughout the experiment, there were times when I started and stopped the timer either too early or too late. This error can be corrected by having a camera video the issuance; I could then go back and analyze the tape for the correct times. Another source of error is the fact that the amount of water I used varied marginally each time and was measured by eye. This error can be rectified by using a constant amount of water in each trial. An additional source of error is the fact that the holes were created manually with an electric drill, which means that they were not perfectly circular; this error can be corrected by using a laser to cut a perfectly circular water hole in the cap of the water bottle. The last source of error is the fact that my bottle was not perfectly perpendicular to the ground—i.e., it would vary by a couple degrees. This could be improved by having a machine flip the water bottle, so that the bottle is orthogonal to the ground.

Links: .:. Top

https://www.researchgate.net/post/Does_flow_rate_discharge_decrease_when_diameter_increases - Discussion about a similar experiment.

https://cdn.ymaws.com/www.eps.org/resource/collection/016775D4-8888-474D-887F-3E33AEA5E6D0/EPSPED_MUSE_bot_holes.pdf - Research paper discussing similar topics.

https://physics.stackexchange.com/questions/358258/hole-in-a-water-bottle - Discussion about differing pressures.

https://en.wikipedia.org/wiki/Surface_tension - Wikipedia page for surface tension.

http://hyperphysics.phy-astr.gsu.edu/hbase/surten.html - HyperPhysics description of surface tension.