Evan Malhi

Spring 2019

Basketball is a sport that has been played around the world for decades. There are so many ever-changing pieces to the sport, such as the size of the court, play style, size of the backboard, color of the backboard, etc. However, one thing that has stayed nearly the same throughout time is the ball. It is has always been played with a ball and always will be. The size of the ball has nearly stayed the same throughout time as well.

The sole thing that is crucial for the ball to function is the air which is pumped into the ball. Too little air and the ball will be flat and won’t bounce enough for the game to be played efficiently. Too much air and the ball will be too hard and it will be difficult to grasp as well as bounce too much. One way that air in the ball can be measured by the air pressure. Therefore, it is important to assess how air pressure can affect the rebound height of the ball.

This experiment will research the relationship between the air pressure inside a basketball and its rebound height.

Procedure and Design: Back to Top

Materials:

● Official Sized Basketball (29.5 inch circumference)

● Air Pump with Pressure Gauge in PSI

● Meter Stick

● Phone Camera to Record

● A Flat Surface

● Someone to Help Hold Meter Stick

To begin, take the pressure of the basketball down to 5.5 PSI using the pump with the pressure gauge. Then get a partner to hold the meter stick straight up with the one end touching the ground. Line up the basketball so that the bottom of the ball is in line with the top of the meter stick. Hold phone camera and start to record a video where the whole meter stick and ball are in the frame. Then drop the ball and be sure to try to put as little outside force as possible on to the ball. Wait for the ball to drop and and bounce back up once. When the ball has bounced up once, stop the video and look at the video to determine how high the ball was at its peak after the bounce. Record this, in centimeters, as the first trial rebound height for 5.5 PSI. Repeat these steps until 5 trials are obtained for the current pressure. Then increase the pressure by 0.5 PSI and repeat steps. Keep repeating steps until data is gathered through 9 PSI.

In this experiment, I will be testing how the pressure inside a 29.5 inch circumference basketball affects its rebound height. The independent variable will be the pressure inside the basketball as it will change as more air is pumped in. The dependent variable will be the rebound height of that basketball as that depends on the pressure. By dropping each ball from the same height, I am making sure that my data is as accurate as possible. I chose to record to the centimeter, not the millimeter, because it is easier to see the centimeter marks in the video than it is the millimeter marks.

Data Analysis: Back to Top

Table 1

Pressure (PSI)	5.5	6	6.5	7	7.5	8	8.5	9
Trial 1 (cm)	23	32	38	45	52	59	64	69
Trial 2 (cm)	22	31	40	43	54	60	64	70
Trial 3 (cm)	23	34	38	45	55	57	65	68
Trial 4 (cm)	24	33	37	46	53	57	66	69
Trial 5 (cm)	21	33	39	44	54	59	64	71
Average (cm)	22.6	32.6	38.4	44.6	53.6	58.4	64.6	69.4

Figure 1 Back to Top

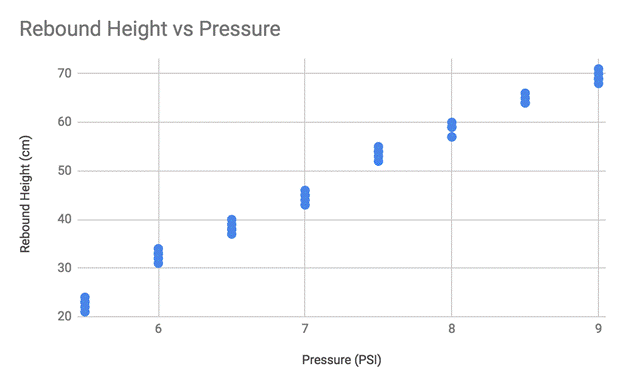
Chart

Figure 2 Back to Top

Data File: Text .:. Excel

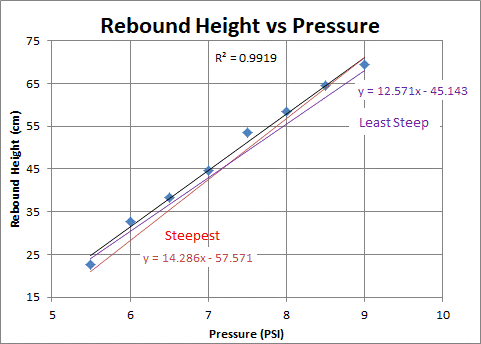
Table 1 shows the data that was collected for each pressure during the experiment. These data points were then averaged to get the average rebound height. Figure 1 displays the rebound height for each trial on one scatter graph. There are five points for each pressure. While there is not a lot of change in the rebound height between trials, there is still some. Figure 2 displays the average rebound height for each trials on one graph with a trend line (black line) through the points. The coefficient of determination, which is 0.9919, is taken from this line of best fit. There is also the most steep line (red line) which connects the smallest rebound height to the largest rebound height. Conversely, there is the least steep line (purple line) which connects the highest rebound height for the lowest pressure with the lowest rebound height for the highest pressure.

Since the coefficient of determination is so close 1, this means that the dependent variable, the rebound height, can be easily predicted from the independent variable, the pressure in the ball. By taking the square root of the coefficient of determination, I can find the coefficient of correlation, which is 0.9959. This means that an increase in the independent variable, the pressure in the ball, has a strong increase on the dependent variable, the rebound height. This can also be seen in the trend line in Figure 2.

In addition, the slope of the steepest and least steep line show the effect that the pressure has on the rebound height. The slope of the least steep line is 12.571. This means that for every PSI the pressure increases, the rebound height increases by 12.571 cm. Conversely, the slope of the steepest line is 14.286. This means that for every PSI the pressure increases, the rebound height increases by 14.286 cm. Therefore, based off of my results, the rebound height of a basketball will increase somewhere between 12.571 cm and 14.286 cm for every PSI the pressure in the ball is increased. If the pressure decreases, then the value the rebound height decreases by is the same as when it increases.

Conclusion: Back to Top

It can be seen that the linear model fits the data very well, given that the coefficient of correlation is 0.9959.

A possible experiment to go off of this one would be to see how much the type of surface the ball is bouncing off of affects the rebound height. I did my experiment on tile in my house but one could test it on a basketball court, blacktop, carpet, etc. I would assume that bouncing the ball off of surfaces such as carpet will cause a much smaller rebound height than bouncing it off of a basketball court or a blacktop.

One way to make the experiment stronger would be if there is a very precise way to measure the pressure. While I did use a pump with a pressure gauge, there is always the possibility that the gauge could be slightly off or that I did not get the pressure to exactly where it needs to be. I think if this is done it will make the trend in the data even more linear than it is now. Also I think there are much better way to find the exact height that the ball rebounded. While I think my procedure was very good, there are improvements that could be made if better resources are available. Also, I used the slow motion feature on my phone’s camera to try and capture as many frames per second, but if one was able to use a better camera they could capture more frames to get the data to be more accurate and possibly be able to record down to the millimeter depending on the clarity of the video.

In addition, it is inevitable that there is a miniscule change in pressure with each bounce of the ball. Even though this difference is very small, it could possibly have had an effect on the data after multiple bounces. It was also pertinent to make sure that no force was exerted on the ball when it was dropped. While this was nearly impossible for one to do, it is something that could be improved about this experiment in the future. One could develop some sort of apparatus that could drop the ball without exerting any force on it.

In conclusion, the results of this experiment were as I expected. The pressure inside the ball has a great influence on the rebound height of the ball and both increase and decrease together.

Links: Back to Top

https://www.livestrong.com/article/411163-does-air-pressure-affect-the-bounce-of-a-basketball/ - General overview of what could affect the rebound height

https://www.scientificamerican.com/article/surface-science-where-does-a-basketball-bounce-best/ - Really good experiment that is basically the same

https://www.researchgate.net/figure/The-basketball-rebound-height-with-varying-internal-absolute-pressure-when-dropped-from_fig8_274248017 - Good graph of what happens when pressure is changed

http://cssf.usc.edu/History/2002/Projects/J0204.pdf - Very professional experiment done in California

https://wright.nasa.gov/airplane/pressure.html - Definition of pressure in an area with force