The Effect of A Trebuchet’s Counterweight on the
Distance Traveled by the Projectile. Introduction| Background
| Method | Results | Analysis | Conclusion | Bibliography | Return to
Research
Before modern weaponry like missiles and guns, other weapons and
mechanisms were used to wreak havoc on a battlefield. One such weapon was the
trebuchet, and specifically this experiment involves counterweight trebuchets.
Simply put, the counterweight trebuchet uses any matter of weight to provide
the force needed to fling projectiles at enemy ranks or castles. It was thought
when using trebuchets, the greater the mass of the counterweight that was used,
the farther and more destructive force the projectile would then have. This
brings up the topic of investigation of the experiment, if the counterweight of
a trebuchet is continually increased, does the distance of the projectile
increase at a constant rate or does the projectile eventually reach a limit.
History is a subject that I have always had mixed feelings about,
because some parts of history are somewhat bland with not much going on in
terms of action, while others have rapid improvement of technology and weapons
that are used in major battle. I personally love any part of history involving
any type of turmoil that includes plagues, wars, or just a simple battle,
because in times of great loss, human kind get creative in all sorts of ways.
This creativity in the art of warfare has always intrigued me, therefore when
deciding the experiment for this internal assessment, I tried thinking of
technology that included physics and eventually found myself face to face with
the trebuchet. The idea came to me when remembering a demonstration of a real
trebuchet, and I decided to use this experiment to begin to understand the
physics behind the trebuchet.
A trebuchet is a type of catapult, which is a common type of siege
engine, which incorporates the use of a swinging arm to “throw” a projectile.
The first trebuchet appeared in Ancient China during the 4th century BC, which
used manpower to swing the arm. However, the more efficient counterweight
trebuchet appeared around the Mediterranean in the 12th century and later
spread to China in the 13th century. Counterweight trebuchets use gravity as
its driving force, specifically; they use potential energy, which is stored by
slowly raising the counterweight attached by a hinged connection to the shorter
end of the beam. Once the counterweight is in place, the trebuchet can be
loosed and the force causes rotational acceleration of the beam around the axle
of the trebuchet. Newton’s Third Law is an important force of the trebuchet
because the action of the falling counterweight sends an equal reaction of the
arm beginning to spin forward. The sling, which holds the projectile, starts
rotating with the beam and since the sling has to swing farther due to it being
placed on the longer end of the arm, must move faster thereby transferring the
increased speed to the projectile being carried. As the arm swings forward, the
projectile is eventually thrown at the optimum angle based off of its placement
on the arm and soars through the air, while the arm can continue to swing
forward at full speed. This means that none of the power is lost from stopping
slightly earlier, which is a common issue with other siege weapons such as
catapults. While the trebuchet slowly faded away from the battlefield after the
introduction of gunpowder, the trebuchet is still a revolutionary piece of
machinery that terrorized every enemy that they faced.
If the mass of the counterweight of a trebuchet is increased at a
constant rate, then the distance that the projectile is thrown will increase
until a point because the weight that is added will only be a small fraction of
the total weight thereby adding little to no extra distance.
Variables:
Independent Variable:
- Mass of Counterweight (Kilograms)
Dependent Variable:
- Distance Traveled by Projectile
After Release (Meters)
Controlled Variables:
- Length of Sling Holding Projectile
- Angle of Release After Fine Tuning
Before Experiment
- Same Level of Damping on Joints
- Constraint Level on Joints
- Shape of Projectile
- Shape of Counterweight
Methodology: Top
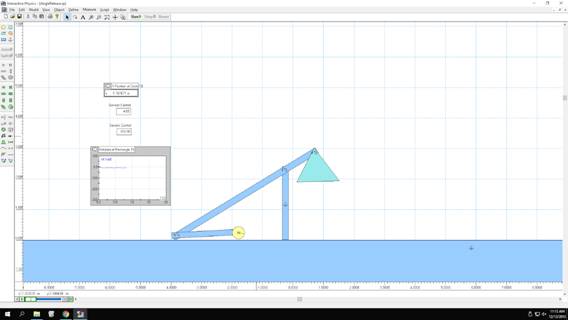
The program that will be used for the experiment is “Interactive
Physics” which allows for a virtual trebuchet to be created and programmed. By
using a virtual model of a trebuchet, many factors such as wind resistance and
pressure differences could be negated, thereby giving more accurate results. A
preexisting trebuchet model is used for the base of the experiment and several
aspects of the program are slightly altered to best fit the experiment. First,
new dampers are programmed onto the different joints of the trebuchet to
eliminate extra rotational forces that break the constraints put onto the
program. Using different constraints on when the trebuchet can release the
projectile and give it a maximum distance also altered the optimal angle of
release. In addition, to make the data gathered more accurate, constraints were
added to stop the projectile once it reached the x-axis, which was being used
to simulate the ground. These constraints stopped the projectile in order for
an individual to measure the distance accurately. Once all of the programming
and added constraints were completed, the experiment could begin by hitting the
run button on the program after setting the specific mass of the counterweight.
Each data point was then recorded onto Microsoft Excel for the eventual data
table and graph creation.
Picture of Trebuchet: Top
Equations to Support:
A trebuchet is a device
that converts potential energy to kinetic energy:
Mgh=12mv2
From basic physics we know
that the range of a projectile with initial velocity v and angle α is:
R=2v2sincosg
Thus, the maximum
theoretical range of a trebuchet is given by:
RMax=2McwMph
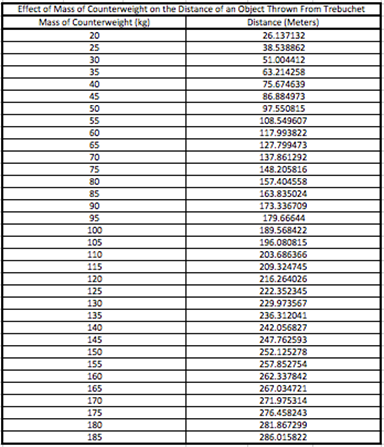
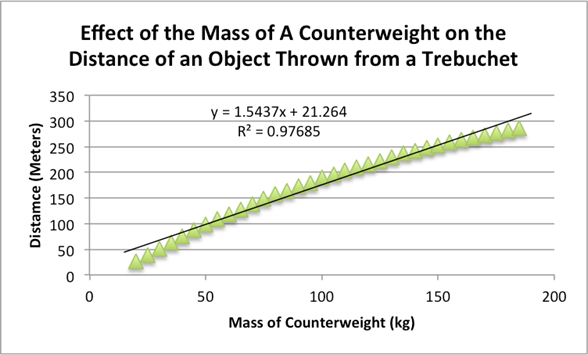
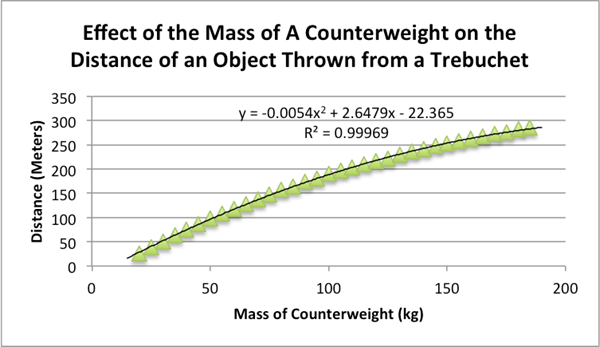
From the data provided by the experiment, two different graphs
could be produced with a linear equation and a polynomial equation each with
its respective correlation coefficient. While at the beginning of the data
collection process, the line of best fit appeared to be linear, but as more
data points were acquired the data clearly showed that this was not the case.
For the amount of data points acquired in the experiment, the higher
correlation coefficient of the polynomial equation of 0.99969 allows for
extrapolation of data points not calculated much more reliably then the linear
model with a correlation coefficient of 0.97685. The equations above correspond
to real life trebuchets, and while we can calculate some of the variables like
velocity with the information known from the program, the angle of release and
the height of the trebuchet were not calculated within the program. However,
these equations would be of use if the experiment were trying to calculate
either the velocity or the angle of release if additional programming was added
to the simulation in “Interactive Physics.”
Conclusion: Top
It is evident that the polynomial model fits the data of the
experiment the best, as seen by the higher correlation coefficient. The model
would allow for extrapolation of more data points, but more recorded data
points would always be more beneficial for an experiment.
However, every experiment has areas where errors could occur and
this experiment was no exception. As stated before, more data points would help
to further strengthen the equations calculated and more clearly identify the
potential limit that the trebuchet could reach. In addition, the trebuchet
simulation that was programmed had an upper limit of 185 kg for the
counterweight because the constraints that helped gather the data would start
to fail due to the high rotational forces that incredibly heavy counterweights
would exert upon the program. This could be remedied by running more extensive
tests on the simulation to make sure that the program could function at higher
weights. Further testing the program could perhaps bring the beginning weight
down from 20 kg because the simulation wouldn’t function for any weight below
20 kg. If the trebuchet were also programmed to identify the different lengths
and materials that the trebuchet was constructed out of, it would allow for
more complex calculations to determine other factors such as optimal angle of
release.
If these errors were to be fixed in a future experiment, it would
be interesting to calculate whether or not different designs of trebuchets
could greatly affect the results of the distance of the projectile. Overall, I
was surprised by the results of the experiment and I am glad that the
experiment gave me an excuse to learn more about physics and history in an
engaging way.
Danielsson, Mats. “What
Is the Physics Behind a Counterweight Trebuchet?” COMSOL Multiphysics©, 11 Oct.
2017, www.comsol.com/blogs/what-is-the-physics-behind-a-counterweight-trebuchet/.
“Trebuchet.” Medieval Squires, Mar. 2018, www.medieval-life-and-times.info/medieval-weapons/trebuchet.htm.
“Trebuchet Physics.” Real World Physics
Problems, www.real-world-physics-problems.com/trebuchet-physics.html.
1.
www.medieval-life-and-times.info/medieval-weapons/trebuchet.htm
This website assisted in the background information of trebuchet and how they
are built.
2.
www.real-world-physics-problems.com/trebuchet-physics.html
This website explains the physics behind a trebuchet with some helpful diagrams
and explanation.
3.
www.comsol.com/blogs/what-is-the-physics-behind-a-counterweight-trebuchet/
More explanation behind the physics with some animations to assist.
4.
https://classes.engineering.wustl.edu/2009/fall/ese251/presentations/(AAM_13)Trebuchet.pdf
A presentation of sorts that goes into detail behind more information about the
trebuchet.
5.
https://hackaday.com/2019/05/20/make-physics-fun-with-a-trebuchet/
Has an interesting video and different experiment involving trebuchets with a
more technological approach.