Tegan Johnson

Effect of Mass on the Regelation of Ice

Introduction Δ Procedure & Design Δ Data Analysis Δ Conclusion Δ Bibliography Δ Other Links Δ Return to Research

Introduction: Go Up

Why is ice so slippery? Up until the 1950s, it was believed that pressure melting was the cause; however, in the 1850s, scientist Michael Faraday believed he had realized the real, physical cause. Faraday thought there was a very thin layer of liquid water on the surface of ice at all time (Faraday); his theory revealed the ease of skating on ice and skiing on snow in way that pressure melting could not explain fully, and Telford and Turner (1963) conducted experiments of their own in a more controlled way later on to prove his theory (Telford) in the most detailed investigation of his theory before the 1970s (Hobbs).

Faraday’s theory makes it possible for regelation (the freezing of water after pressure causes it to melt) to occur; as pressure is applied to the ice and melts it, the water above the surface of the ice refreezes (Yen). Professor Bottomley of Glasgow University performed an experiment in 1872 looking into Faraday’s claims before they were universally accepted. He hung a piece of wire with weights on the ends over a chunk of ice, and hours later, the wire had worked its way through the ice (“On the Melting…”). The ice was slightly marred by the wire’s passage, but he was not able to break the ice along the line.

His experiment fascinated me, so I want to recreate it and investigate how the mass of an object hanging by a wire changes the speed at which it completely passes through a block of ice. I believe that the more weight I add, the faster regelation will occur because the more weight put on the ice, the more pressure will be exerted, thus melting it quicker. Examining the relationship between the mass and time will also be interesting—I don’t know if they are related linearly or exponentially. After collecting data, I will use Microsoft Excel to determine which regression line fits my data best.

Procedure and Design: Go Up

Materials:

● 24 gauge galvanized steel wire, 0.51 mm in diameter (± 0.005 mm)

● 2 inch brass pipe, 5.08 cm diameter (± 0.005 cm)

● Varying weights, 0.5 kg to 2.5 kg (± 0.0005 kg)

● Timer

● Way to record time (iPod Touch)

● 2x4 wood with 1 cm wide notch for balancing ice (± 0.05 cm)

● Water

● Freezer to freeze water (-17.5 ℃ ± 0.05 ℃)

● Way to contain experiment (5 gallon bucket)

Weeks before I started collecting any data, I filled a brass pipe (with a rubber stopper on one end) with water and after they froze, I would ease the cylinder out of the pipe and cut it into three or four sections. Those would be kept frozen until I would actually experiment with them. To test the regelation time period, I had a timer in a bucket with my iPod touch taking a time lapse resting on the notched 2x4 laying across the bucket. I made a large loop with wire and attached varying weights to it, making sure they were secure and would not fall off; I then hung the loop across an ice cylinder resting on the wood and started the timer at the same time I let go of the wire. After a couple hours, I would check on the ice to see if the wire had worked its way through, and if it had, I would record the time on the time lapse at which the weights hit the bottom of the bucket.

Variables:

In my experiment, I will test how many minutes it takes for a weighted 24 gauge wire to pass through a 5.08 cm diameter cylinder of ice. Every piece of wire used will be 24 gauge, and every block of ice will be 5.08 cm in diameter. The independent variable will be the mass of the weight attached to the wire; I will wrap the different masses to the wire for each trial. The dependent variable will be the time it takes for the wire to pass through, from when I set the wire on the ice to when the weights hit the bottom of the bucket. By starting my timer at the same time when the wire’s full weight rests on the ice and watching the time lapse video for when the weights fall to the bucket, I can obtain a fairly accurate time of regelation. I chose to record just how many minutes, not down to the seconds, because my time lapse would not give an adequate recording. In addition, in my preliminary tests, each of the different weights fell several minutes apart; it was clear that rounding to the seconds was sufficient. (I rounded results 0-29 seconds down and 30-59 seconds up.)

Data Analysis: Go Up

Logarithmic regression line

y = -98.2ln(x) + 137.45

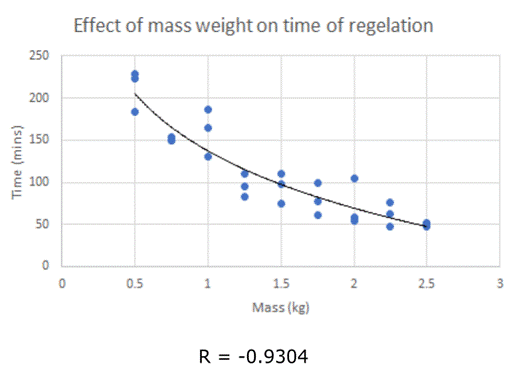
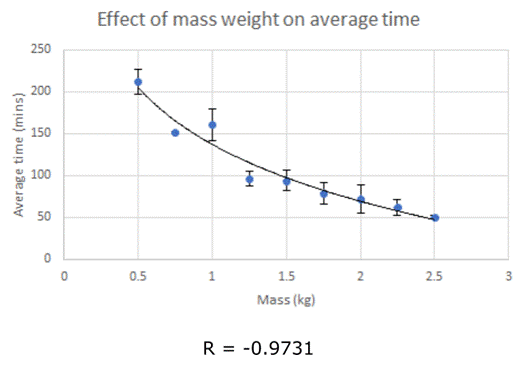
Screenshot (1).png Screenshot (2).png

Data file:Text Δ Excel

The negative logarithmic regression line fits my data very well. The correlation coefficient for the graph of averages is -0.9731, so I can assume that y = -98.2ln(x) + 137.45 is an accurate approximation to the regelation time of kilogram masses going through a 5.08 cm diameter block of ice. The data points at 0.75 kg and 1 kg seem odd; one of them is most likely an outlier, but I cannot say for sure which one. I presume the average time I found for the 1 kg mass is an outlier because it doesn’t fit the regression line as well as the time for the 0.75 kg mass, but finding outliers in this case is beyond the scope of this experiment. I don’t believe I have enough data to determine whether a measurement is an outlier, or what kind of skew an outlier would have on my results, but it seemed important to note the abnormalities.

I can interpolate values between 0.5 kg and 2.5 kg somewhat confidently, because I already have data points within that series and can reasonably infer the outputs of those values; despite that, extrapolating less than 0.5 kg or beyond 2.5 kg might prove to be problematic and unreliable. It makes sense that as the mass of the weights increase, the time of regelation will decrease (following the model), but it is nearly impossible to find an equation to accurately model the nature of ice—as the mass of the weights get closer to 0, the ice will melt entirely before the wire works through the ice underneath, so having the time of regelation near infinity is not possible. Additionally, the regression line crosses the x-axis at about 4 kgs, but I think it’s impossible for the time of regelation to be less than 0 minutes. While the logarithmic regression line might fit the given data reasonably well, an exponential graph could more accurately represent the nature of regelation.

Exponential regression line

y = 272.67e^-0.682x

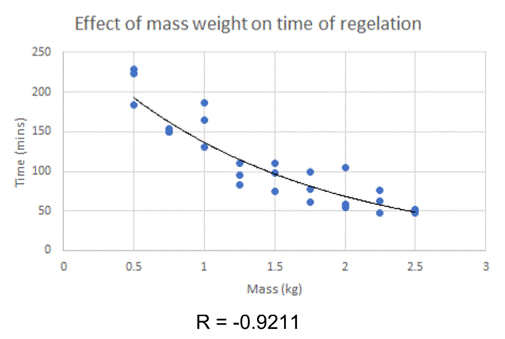
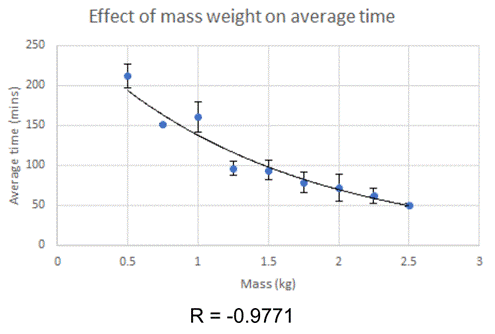
Screenshot (4).png Screenshot (5).png

Data file:Text Δ Excel

The exponential regression line y = 272.67e^-0.682x fits my data better than the logarithmic line. The correlation coefficient for the exponential regression line of averages is -0.9771, which is better than the logarithmic one. This trendline better represents regelation; it never crosses the x-axis, so the accuracy is improved there. However, there is no horizontal asymptote at the y-axis (it crosses at 272.67 minutes), meaning there is a maximum time period for regelation to occur. I don’t think any graph could accurately describe what happens as time mass approaches 0 minutes; there must be a restricted domain.

Because this regression line shows the nature of regelation better than the logarithmic model, any extrapolation beyond 2.5 kg could be more reliable. Nevertheless, as is always with extrapolation, any calculations with values outside of my experimental data are still dubious, but probably more accurate than those with my logarithmic line.

Semi-log graph

Data file:Text Δ Excel

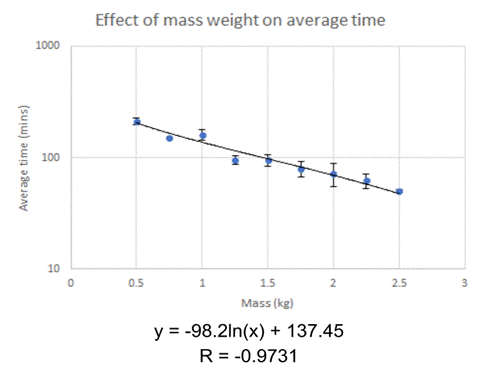
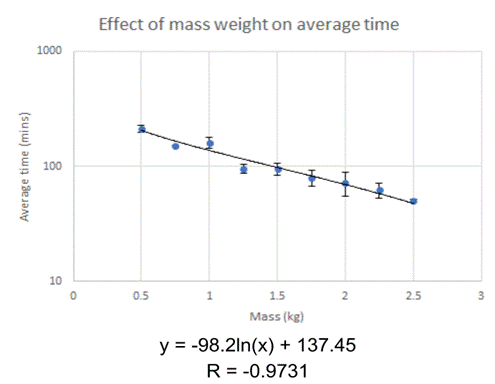
By graphing my data on a semi-log plot (changing the y-axis to a log scale base 10), it is clear that there is an exponential relationship between the mass and the time of regelation. The semi-log plot demonstrates this relationship by showing the data in a line that appears linear due to the change in scale on the y-axis. While this trend obviously cannot go on as the domain increases, for the data I’ve collected, this is a suitable representation of the connection between mass and time.

If I were to scale both of the axis on a log scale, making it a log-log plot, my data would not appear linear. The semi-log plot displays the trend of the data in a more useful way.

Calculating pressure

Using the formulas and , I can find how much pressure the wire was exerting on the ice. If one half of the wire is laying on top of one half of the ice cylinder, the total area can be calculated by multiplying half of the circumference of the wire by half of the circumference of the ice.

½π(0.00051) * ½π(0.0508) = 6.392542771*10^-5

Therefore, using , the pressure for the each of the masses is:

Mass (kg)	Pressure (kPa)
0.25	38.365
0.50	76.730
0.75	115.095
1.00	153.460
1.25	191.825
1.50	230.190
1.75	268.555
2.00	306.920
2.25	345.285
2.50	383.650

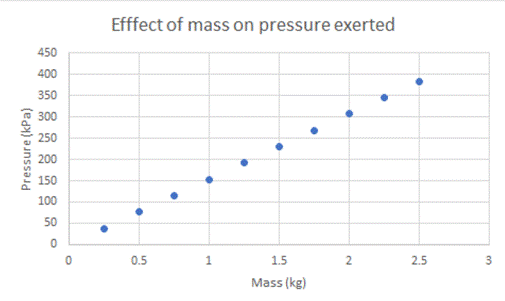
Screenshot (8).png

Data file:Text Δ Excel

Understandably, this relationship is linear.

Conclusion: Go Up

It is evident that the exponential model fits the nature of regelation in my experiment, as seen by the higher correlation coefficient and the semi-plot plot. I believe some extrapolation to other sized weights could be considered, but the scope of my experiment is quite small.

It would be interesting to see how different types of wire cut through ice differently, either by changing the speed at which regelation occurs or the size of the marred ice. Wire made out of a different metal, like copper, would move through the ice faster because it has better thermal conductivity than the galvanized steel wire I used. Testing the time it takes for regelation to occur in different temperatures; I would assume that a high temperature would cause it to occur faster.

This experiment would definitely be stronger if I included more trials. Because of the time constraint I was under, the number of trials and variations I tested was very limited, and I understand that my conclusions are therefore limited and do not have a high degree of confidence. My method of finding data was also not exactly error-free: I’m not sure about the accuracy of my digital stopwatch, as it’s over 20 years old, and in addition, the temperature of my garage actually changed throughout the experiment, something I didn’t notice until after I collected all my data. It started out at 4.5-5.5 ℃, but as the weather outside warmed up, the garage temperature rose to 8.5 ℃ by the end of the experiment. This would mean that the ice was melting already as the wire was pushing through, thus making the diameter of the cylinder smaller.

Many of the ice cylinders I cut had irregularities (like air bubbles within the ice or uneven surfaces), so I avoided using the especially misshapen or bubble-filled ice; however, it was impossible to find cylinders without any air bubbles. I used tap water to fill the cylinder and froze them for several hours in my freezer (at -17.5 ℃, the same temperature at which the wire was placed on them), and the water in my area is very soft, and my sink aerates the water coming through the faucet. I tried boiling the water to remove trace minerals and air molecules, but the ice made from boiled water did not look any different from water straight from the tap. I would assume that finding a way to eliminate these air bubbles, perhaps by freezing from the top down using a cooler in my freezer, would make my data more reliable. Even so, I am satisfied with my ice cylinders, as they more closely mimic ice in nature, full of irregularities.

Overall, I am still amazed at what regelation can do. I had never heard of it before until a few months ago, and seeing it in action was incredible. The cylinders of ice that the wire worked through were only slightly marred by its passage, and I was unable to break the ice along the line. I have included picture of this phenomenon to show its surprising nature.

Bibliography: Go Up

Faraday, Michael. “Letter 3530.” The Correspondence of Michael Faraday, Volume 5: 1855-1860, IET, 2008.

Hobbs, Peter Victor. Ice Physics. Oxford University Press, 1974.

“On the Melting and Regelation of Ice.” Pacific Rural Press, 16 Mar. 1872, p. 163.

Telford, J.W. and J.S. Turner (1963). “The motion of a wire through ice.” The Philosophical Magazine, vol. 8, p. 527-531.

Yen, Yin-Chao. Review of Thermal Properties of Snow, Ice and Sea Ice. UNITED STATES ARMY CORPS OF ENGINEERS, 1981, p. 6.

Introduction: Go Up

Procedure and Design: Go Up

Materials:

Variables:

Data Analysis: Go Up

Logarithmic regression line

Exponential regression line

Semi-log graph

Calculating pressure

Conclusion: Go Up

Bibliography: Go Up

Other Links: Go Up