The Consequences of a Changing Trebuchet Counterbalance
By Migdalia “Midge” Pensado
Table of Contents: Background >>>> Materials >>>> Method >>>> Diagram >>>> Data >>>> Graph >>>> Conclusion >>>> Bibliography/Related Sites >>>> Back to Research
The trebuchet was known in the Middle Ages as a terrifying war machine that laid siege to seemingly indestructible castles and forts across Europe. The path of destruction that they created was fearsome enough for individual trebuchets to earn their own names such as “‘God’s stone thrower,’ ‘the daughter of the earthquake,’ ‘big mother,’ ‘war wolf,’ and the ‘bad neighbor’” (Farrell). Unlike their catapult predecessors, the trebuchet was more accurate and more powerful, capable of throwing stones up to one ton over the distance of three football fields or more. The trebuchets themselves had throwing arms up to 60 feet long, and needed a team of twelve men to load, wind, and launch rocks, hot sand, diseased bodies, Greek fire, darts, and even excrement at enemies.
These fearsome machines had a throwing arm that was weighed down with a hinged counterweight that would swing down, and propelling and opening the leather pouch on the opposite end of the throwing arm towards whatever it was aimed at.
The counterweight is an important part of how the trebuchet is able to launch so far. It always needs to be heavier than the projectile being thrown so it can fall and move the arm. It could be possible to manipulate the mass of the projectile, but when engineers in the Middle Ages tried to construct these massive war machines, it was a guessing game to see what size counterweight would work the best for the trebuchet. Counterweights that were too light wouldn’t swing down as hard as one that was heavier, and even then if it was too heavy, it could stress the frame too much.
Statement of the Problem: The purpose of the investigation is to investigate the effect of the mass of counterweight on how far the constant projectile is thrown.
Hypothesis: I believe that the decrease in the mass of the counterweight of the trebuchet will result in a shorter measured distance thrown of the constant mass because there will be less mass and thus less inertia than a bigger counterweight. Distance is defined as the measured length from the trebuchet and where the constant throwing mass lands after being launched. Controlled variables will include the trebuchet itself, the launching location, and the throwing mass. The dependent variables will be how far the projectile mass will be thrown, and how long it will be in the air.
● Trebuchet
● Tape measure
● Baseball
● Weights the kilogram increments of 1, 2, 2, and 5
● Makeshift cart made from a wide plank of wood and wheels
● Rope
● Pencils
● Notebook
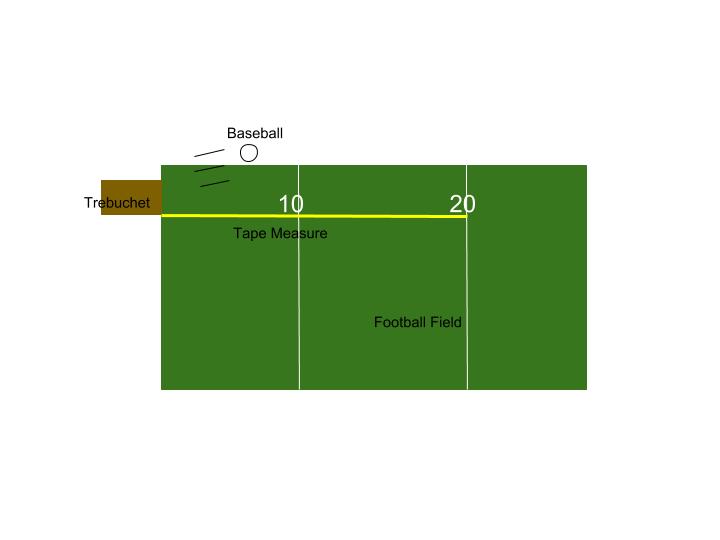
Method: The trebuchet is placed and tied to the cart and rolled up to the football field and was lined up at the line that represented zero yards, and taken off the cart. A tape measure was then rolled out alongside the trebuchet, and staked to the ground with a pencil to prevent any movement that can change the measurements taken. The counterweights are changed for each round of three trials, and the holder for the weights did count in the final counterweight mass due to the fact that it weighs one kilogram itself. The baseball is then placed in the pouch to be launched and the crater made in the football field with the impact is then measured from the center, and recorded in the notebook.
Figure 1: The trebuchet

Figure 2: Aerial arrangement of experiment on football field (not drawn to scale)
Data Table:
Figure 3: Raw Data
|
Counterweight (kg) |
Distance (m) |
|
1 |
0 ± 0 0 ± 0 0 ± 0 |
|
2 |
0.9 ± 0.34 0.61 ± 0.34 0.22 ± 0.34 |
|
3 |
0.96 ± 0.15 1.34 ± 0.15 1.26 ± 0.15 |
|
4 |
1.87 ± 0.09 2.47 ± 0.09 2.05 ± 0.09 |
|
5 |
2.7 ± 0.38 2.06 ± 0.38 1.94 ± 0.38 |
|
6 |
4.63 ± 0.415 4.12 ± 0.415 4.95 ± 0.415 |
|
7 |
6.4 ± 0.675 4.91 ± 0.675 5.05 ± 0.675 |
|
8 |
5.81 ± 0.265 5.47 ± 0.265 5.28 ± 0.265 |
|
9 |
5.12 ± 0.185 5.62 ± 0.185 5.49 ± 0.185 |
|
10 |
6.88 ± 1.095 7.68 ± 1.095 9.07 ± 1.095 |
Figure 4: Average distances of each counterweight
|
Counterweight (kg) |
Average Distance (m) |
|
1 |
0 ± 0 |
|
2 |
0.576 ± 0.34 |
|
3 |
1.186 ± 0.15 |
|
4 |
1.49 ± 0.09 |
|
5 |
2.3 ± 0.38 |
|
6 |
4.56 ± 0.415 |
|
7 |
5.453 ± 0.675 |
|
8 |
5.52 ± 0.265 |
|
9 |
5.41 ± 0.185 |
|
10 |
7.876 ± 1.095 |
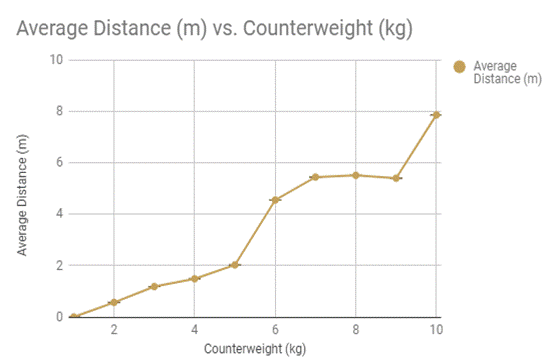
The mass of the counterweight did have a significant effect on how far the projectile was thrown. For example, the the one kilogram weight was too light to have any impact on the throwing distance at all, but when the weight was doubled to two kilograms, the ball was actually able to be lifted off the ground and launched a modest distance. This distance generally increased as the counterweight increased as well. I say this because my biggest assumption in proving my hypothesis would be that the distance would then increase in a linear fashion of the regular intervals that the counterweights were increasing in, and that wasn’t the case because of the measurements of the average distances of the eight and nine kilogram counterweights that seemed to have gone backwards in the trend. The distance also spiked with the addition of the six, and ten kilogram counterweights as well, making this a more nonlinear graph than I expected; it had more of a curve with spikes and drops than I originally expected. This could have been a fluke in the how the average was calculated because of the varying values in the actual measurements that were recorded while out at the field, or a more complex relationship with the weights than I imagined. At first, when the counterbalance was increasing to five kilograms, the average distance increased steadily in a linear fashion, only to spike at six kilograms, slowly rise until a slight decrease in the distance at nine kilograms, and spiking again at ten. This could be due to the fact that these are only the averages, and that the range of the results calculated to reach this could have thrown the data in for a loop. As for an infinite mass, it would be the same as nothing because they would accelerate the same as gravity, so there is some consistency in the experiment.
As for errors that might have occurred in the measurements recorded, what was possibly a factor in how different the data was that it was gathered over the span of two different days: the first day started out relatively dry until it ended in rainy weather, while the second was sunnier and much more clear out. The water from the rain the first day could have changed the way the wood of the trebuchet worked during the launches, like how well the arm could move and throw the baseball. Even the wind could have played a role in how far the ball was thrown.
Another source of error could have also been the minute movement of the tape measure as I used it to gather the measurements. I am unsure one how much this could have affected the data, since the end of the tape measure was firmly staked down, and didn’t give me much trouble. I calculated the varying amounts of error for each trial, and it seems that error increased as the distance that the projectile distance grew. This could account for the spike in the graph of the data, or could account of the air resistance the ball experienced as it flew through the air longer distances each time, and that could have affected the data.
As for improvements for this experiment, I would definitely start by conducting this during a time when the days are longer and would therefore allow me to gather all my data at once, instead of being spread out over the course of two different days. I would also try to find a way to make the launch smoother, maybe by oiling the trebuchet, or even making one of my own design if time allowed, instead of simply fixing one up from a previous experiment. This way, there would be less friction in the arm that can allow for the falling motion of the counterweight much more smoother as well. The tape measure, even with my certainty about the security of it, could be held down by something much stronger and possibly less mobile, like being taped to the ground.
Despite my troubles and misadventures with my trebuchet, I can say for certain that the mass of the counterweight really does affect the distance thrown for a projectile: the generally heavier, the generally better.
Science Buddies Staff. "Effect of Trebuchet Arm Length or Counterweight Mass on Projectile Distance" Science Buddies. Science Buddies, 28 Oct. 2017. Web. 29 Oct. 2017 <https://www.sciencebuddies.org/science-fair-projects/project-ideas/ApMech_p013/mechanical-engineering/effect-of-trebuchet-arm-length-or-counterweight-mass-on-projectile-distance>
This displays the mechanics of the trebuchet, and how it is possible to build one. ]
Linda, Alchin. “Trebuchet.”
Trebuchet, Lords and Ladies, 2017, www.lordsandladies.org/trebuchet.htm.
This site gives a detailed history of the legend and lore surrounding the
massive real-life trebuchets used in the Middle Ages.
Farrell, Scott. “Arms and Men: The Trebuchet.” HistoryNet,
HistoryNet, 23 June 2016, www.historynet.com/weaponry-the-trebuchet.htm.
This details the history of the weapon, and how it was used in medieval
warfare.
https://www.comsol.com/blogs/what-is-the-physics-behind-a-counterweight-trebuchet/
This explains the
physics behind the trebuchet, and includes helpful demonstrations of virtual
ones being shot.
http://shortsleeveandtieclub.com/designing-a-trebuchet-optimizing-weight-and-length/
More intrsuctions on how to build a trebuchet, and how to optimize the measurements and weights for the best throws.