By: Tyler Lathrop, Mikah Springer, and Sean Chamberlin

Table of Contents: Personal Engagement – Background – Question – Variables – Controlling Variables – Hypothesis – Materials – Procedure – Diagram – Data – Conclusion – Related Links – Bibliography – Return to Research

We chose to do our IA on the effect of frequency on the flame height of a Rubens’ Tube not only because it’s a fun and interesting experiment, but also because we want to know what standing sound waves look like in relation to two different harmonics. Doing this, we hope to discover where there are areas of oscillating pressure (where the flames are lower) and where there are areas of constant pressure (where the flames are higher), and which frequencies cause the pressure to react this way.

Background: Go Up

The discovery of simple harmonic motion dates back to the 1600’s, which was when Robert Hooke was the first to experiment with it. In July of 1664 he calculated the number of vibrations for each musical note leading directly to harmonic motion. Hooke created a law later named after himself and it stated that elastic materials return to their original form after being deformed. The elasticity of an elastic material is the restoring force on the material after deformation. He also said that “simple harmonic motion is a periodic oscillation that is commonly found in nature. For example the vibrations of musical notes.” The equation for Hooke’s law is as follows: F=(-k)(x)

Where:

F = Restoring Force

k = Constant of Proportionality or the Spring Constant

x = Distance from One End of the Spring to the Stretched End

Later, in 1822, French mathematician Baron Jean-Baptiste-Joseph Fourier published a discovery that found the oscillations of musical instruments can be measured in simple harmonic motion. In fact, any regularly repetitive motion and any wave, no matter how complicated its form, can be treated as the sum of a series of simple harmonic motions or waves.

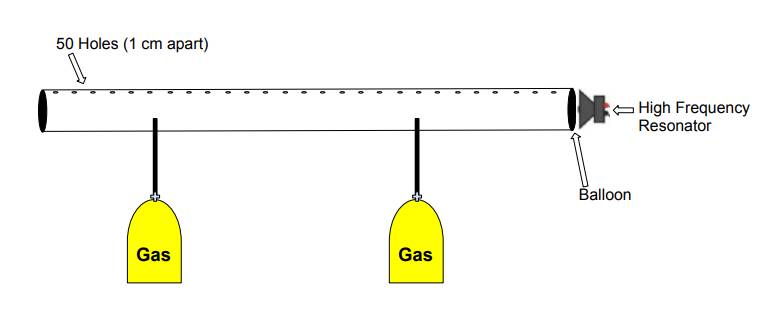
The Rubens’ Flame Tube was invented in 1905 by a German physicist named Heinrich Rubens. The invention was his way of demonstrating acoustic standing waves visually. The first model was built with a 4 meter long brass tube that had 100 2mm holes drilled on top that were spaced 3 cm apart. He sealed the tube so that no excess gas would leak out when it was filled. He then lit flames from the gas leaking through the holes. Because speakers didn’t exist back then, he used a tuning fork to produce the sound going into the tube at one end. Standing waves were produced in the tube which were seen through the change in height of the flames.

Question: Go Up

How does the frequency of sound played (Hz) affect the maximum flame height (cm) in a Rubens’ Flame Tube?

Variables: Go Up

Independent	Frequency (Hz)
Dependent	Flame Height (+/- 0.5 cm)
Controls	Gas source, frequency generator, speaker, airflow, temperature of room

Method of Controlling Variables: Go Up

The gas source, frequency generator, and speaker will be controlled by using the same ones throughout the experiment. The airflow will be controlled by keeping all doors closed during each of the trials to keep the flames from flickering. The temperature of the room will be controlled by testing in the same room and making sure the thermostat is always the same.

Hypothesis: Go Up

Materials: Go Up

One round metal duct pipe (3 x 60 inches)
One plastic or metal end cap (3 inches inner diameter)
Two brass barb MIP adapters (3/8 x 1/4 inch)
Two rubber O‐rings (1/2 inch inner diameter)
Two washers (1/2 inch inner diameter)
One latex hose (60 inches, 3/8 inch outer diameter, 1/4 inch inner diameter)
One latex balloon (12 inch diameter)
One 1/2 inch drill bit, capable of drilling metal
One 1/8 inch drill bit, capable of drilling metal
Speakers with good bass
Electric drill
One roll of duct tape
One roll of masking tape
Scissors
Pliers
Permanent marker
Metal file
Two metal stands
Two propane tanks
Lighter
Ruler
App to generate frequencies

Procedure: Go Up

Assemble the metal duct pipe and place a piece of duct tape down the seam of the pipe. Cut the duct tape so that it reaches right up to the edge of the pipe but does not wrap around it. Be sure that the duct tape is smooth and that there are no wrinkles.
A line of 1/8 inch diameter holes will be drilled along the top of the tube and will be 3/4 inches apart. To make sure that the holes are drilled in a straight line, place a piece of masking tape down the length of the pipe with one edge of the tape along the center of the top of the pipe.
Starting about 8 inches from one end of the tube, make marks every 3/4 of an inch until you get to about 8 inches from the other side of the tube. Use the edge of the masking tape so that all of the marks are in a straight line. There should be a total of 60 marks. Remove the masking tape when all of the marks have been placed.
Use a 1/8 inch drill bit to drill a hole where each mark was made. Be sure that the drill bit is precisely lined up on the mark before the hole is drilled. Since the metal is very thin, some of the holes might have jagged edges. A metal file or pliers may be used to clear up the holes. It is important that all of the holes are clear and round so that the flame heights will be uniform.
Two 1/2 inch holes will be drilled in the side of the tube for gas hoses to be connected. Place two marks on one side of the tube, each about 18 inches from the end of the tube. Use a 1/2 inch drill bit to drill a hole where each mark is located. File down these holes as well.
Locate the two brass barb adapters, two washers, and two O‐rings. Place a washer over the threaded end of each adapter, and then place an O‐ring over the threaded end of each adapter. This will be connected to the side of the pipe and is where the gas hoses will attach.
Screw the threaded end of each barb adapter into the 1/2 inch holes. Pliers might need to be used to tighten the barb and O‐ring down to the pipe. It is very important that there be a tight seal between the O‐ring and metal pipe to ensure that there are no leaks. If the adapter will not thread properly, it might be that the hole needs to be rounded out more with a file or pliers.
Place the cap over the crimped end of the tube. Be sure that it is pushed down as far as possible on the end of the tube. Seal the end by wrapping a piece of duct tape around the cap and pipe. Be sure that the tape is smooth and has no wrinkles.
Locate the latex rubber balloon and use scissors to cut off the end of the balloon. Stretch the balloon over the open end of the tube to form the diaphragm. Be careful to stretch the balloon tightly but not so tight that it will tear against the edge of the tube. Use a piece of duct tape to secure the balloon to the tube.
Locate the latex hose and use scissors to cut it in half. Connect each of the 30 inch hose pieces to the barb adapters that have been installed into the side of the tube. Ensure that the hoses are connected as far up on the adapters as possible so that they have a good seal.
Put two metal stands under each end of the tube to hold it up.
Hook up each tube to a propane source and turn the sources on.
Wait for the tube to fill with gas and then light the top of the tube with a lighter, making sure that every hole gets lit.
Secure a speaker on the end of the tube with the balloon, or hold the speaker up to it.
Use a frequency generator app to find the frequency that creates the highest possible single flame.
Go down from that frequency in 0.5 Hz intervals 17 times, using a secured ruler to measure that same flame height in cm each time.
Go up from the maximum height frequency in 0.5 Hz intervals 17 times, using a secured ruler to measure the flame height in cm each time, making a total of 35 data points (17+the maximum flame+17).
Repeat steps 15-17 with other flame heights that are relative maximums to gather sufficient data.

Diagram: Go Up

Data: Go Up

Data Table 1.0- 112-129 Hz

Frequency (Hz)	Flame Height (+/- 0.5 cm)
112	6.2
112.5	6.5
113	6.7
113.5	6.9
114	7.1
114.5	7.3
115	7.4
115.5	7.6
116	7.7
116.5	7.9
117	8.4
117.5	8.5
118	8.7
118.5	8.8
119	8.9
119.5	9.4
120	9.9
120.5	11.1
121	10.3
121.5	10.1
122	9.6
122.5	9.3
123	8.8
123.5	8.6
124	8.3
124.5	8.1
125	7.9
125.5	7.7
126	7.6
126.5	7.5
127	7.3
127.5	7.3
128	7.2
128.5	7.2
129	7.1

Data File: text .:. Excel

Data Table 2.0- 195-212 Hz

Frequency (Hz)	Flame Height (+/- 0.5 cm)
195	6.1
195.5	6.2
196	6.3
196.5	6.3
197	6.5
197.5	6.6
198	6.8
198.5	6.9
199	7.1
199.5	7.2
200	7.4
200.5	7.5
201	7.5
201.5	7.6
202	7.8
202.5	8.3
203	8.8
203.5	9.1
204	8.7
204.5	8.2
205	7.9
205.5	7.8
206	7.7
206.5	7.5
207	7.5
207.5	7.4
208	7.2
208.5	6.8
209	6.7
209.5	6.6
210	6.4
210.5	6.3
211	6.2
211.5	6.1
212	6

Data File: text .:. Excel

Conclusion: Go Up

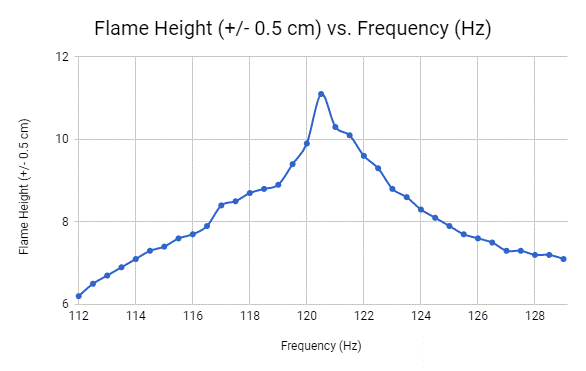
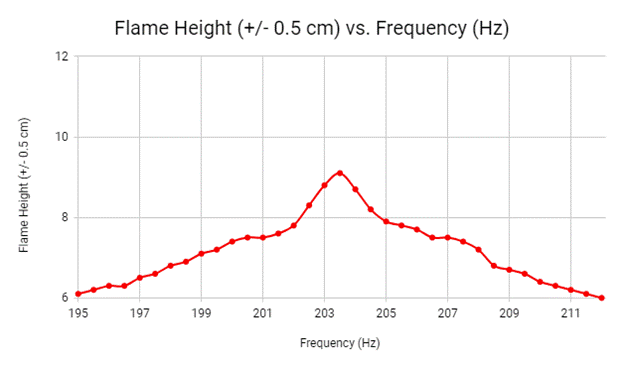
If a maximum flame height is found and the frequency of the sound is altered by 0.5 Hz several times on both sides of the maximum then the flame height will decrease by 0.2 cm for every increment away from the frequency of the maximum flame height. The hypothesis was not confirmed by the data from the experiment, but was very close. When we altered the frequencies by 0.5 Hz, the height of the maximum flame changed by an average of 0.262 cm for the 112-129 Hz frequency range and an average of 0.179 cm for the 195-212 Hz frequency range. The average of these two is 0.221 cm which means that our hypothesis was only 0.021 cm off. There were several instances in each range of frequencies when the flame height changed by 0.2 cm which was predicted by the hypothesis. However, some frequencies made our flame jump 0.5 cm, 0.8 cm, and even 1.2 cm, which was the maximum amount of change between frequencies.

This means that the higher the frequency of the interval, the less difference is seen in the biggest flame height between each specific frequency. Overall, the data tells us that for different frequencies, the height of the highest flame on the Rubens’ flame tube varies, because of the unique sinusoidal wave of each frequency. At the specific frequencies of 203.5 Hz and 120.5 Hz, the peak of the sinusoidal wave was the highest. When decreasing or increasing the frequency in intervals of 0.5 Hz from these peak frequencies the flame height creates a bell curve before repeating again. With this information, we were able to conclude that the overall heights of the flame in the lower range of frequencies were taller than the overall height of the flames in the higher range of frequencies.

The conduction of this experiment had many possible errors that could have affected the outcome of the data. First, the environment in which we conducted the experiment had a draft and as a result the flame height could have been altered. Second, when reading the flame height the flame was flickering so the recorded height was not always completely accurate. Third, the gas pressure inside the tube could have varied depending on how far from the two gas inputs the flame holes were. This brings some of the accuracy of the data down to perception, and leaves a lot of room for error in recording the correct height of the flame.

The way to fix the first possible source of error would be to perform this experiment in a room sealed off with no draft or vents to alter the flame height. The way to fix the second issue would be to use a camera to record the flame height and average the height of the flame over an interval to find a more precise flame height. The way to fix the third issue would be to use more gas inputs and consistent pressures measured with gauges to ensure accuracy.

Related Links: Go Up

prettygoodphysics.wikispaces.com/file/view/How to Build a Rubens Tube.pdf – This is how to build a Rubens Tube.

www.britannica.com/biography/Joseph-Baron-Fourier – History of the Rubens Tube.

www.britannica.com/science/simple-harmonic-motion – How simple harmonic motion works.

http://www.physicsclassroom.com/class/waves/Lesson-4/Formation-of-Standing-Waves – The formation of standing waves.

http://www.bbc.co.uk/bitesize/standard/physics/telecommunications/communication_using_waves/revision/5/ – Frequency, wavelength, amplitude, and wave speed.

Bibliography: Go Up

Brown, Travis. How to Build a Ruben's Tube. 2013, prettygoodphysics.wikispaces.com/file/view/How to Build a Rubens Tube.pdf.

Gardner, Michael. An Investigation of Rubens Flame Tube Resonances. Aug. 2007, www.physics.byu.edu/docs/thesis/27.

Struik, Dirk Jan. “Joseph Fourier.” Encyclopædia Britannica, Encyclopædia Britannica, Inc., 25 Jan. 2017, www.britannica.com/biography/Joseph-Baron-Fourier.

The Editors of Encyclopædia Britannica. “Simple Harmonic Motion.” Encyclopædia Britannica, Encyclopædia Britannica, Inc., 15 Feb. 2017, www.britannica.com/science/simple-harmonic-motion.