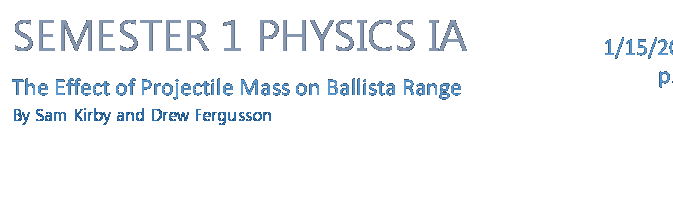
Contents

Introduction

Background

The ballista is a medieval siege weapon that resembles a large crossbow. It was known for being more accurate than a catapult since it fired bolts, but it also had less range₁. It gets it power from two twisted ropes that create tension and allow it to fire low and straight₂. The design is thought to have originated in Ancient Greece, and the Romans later adapted it in approximately 120 B.C.₃. It continued to be used into the 13^th century and beyond. It was used extensively by the French and it featured during the Siege of Dover in 1216₄. Large ballistas were capable of firing projectiles hundreds of yards. Eventually the ballista would be replaced in widespread usage by cheaper and simpler weapons like the crossbow and trebuchet₅.

Generally, slightly heavier projectiles are slightly more accurate due to the fact that they are not affected by wind and other atmospheric conditions. Lighter arrows aren’t affected as much by gravity but also have less momentum and can be affected by the wind. A bow or other firing mechanism can only provide the projectile with a certain amount of force, and the rest is determined by the composition and shape of the projectile₆.

Problem

This investigation in designed to test the effect of projectile mass on the distance that a ballista can fire that projectile.

Hypothesis

If the mass of the projectile that is being fired using the ballista is changed, then the distance travelled will graphically be in a bell curve shape because there will be an optimum mass, and anything lighter or heavier than that will have less range. The mass will be the measure of the inertia of the wooden projectiles that will be used. The range is the horizontal distance travelled by the projectile. Other variables that will be kept constant include the size and shape of the projectile, the location of the experiment, the launch angle of the ballista, and the amount of tension on the ballista.

Method

Materials

In order to perform this experiment, it is required to have a working ballista and a large, flat area where it can be fired safely. Sandbags should also be brought and placed on the base of the ballista in order to prevent movement and make the procedure safer. It is also necessary to have five projectiles with differing masses but identical shape. For example, five projectiles made up of the following types of wood could be used: cherry, walnut, oak, maple and birch. A distance measuring wheel is also necessary to find the distance that the projectile travels. A scale is needed to measure the mass of the wooden projectiles.

Procedure

In order to test the aforementioned hypothesis, the first step is to build or obtain a functioning ballista. This construction can be done in a number of different ways, and guides on how to do so are easy to find on the internet. To begin, measurements for all of the different lengths must be taken from either existing blueprints, or guessing and checking. There are three main steps to fully build a ballista: the first is to build the frame, next build the shaft based on the frame with the winch and the trigger, and finally, build the stand to allow for vertical-horizontal motion. Then, the ballista should be placed on a flat area in a large space and secured with sandbags. With the safety on, use the winch to put the ballista into firing position. Then place the first projectile into the firing slot. Fire the projectile and follow the path of the projectile with the measuring wheel. Record the distance and reload the ballista. Each projectile should be fired and recorded five times to maximize precision. Then repeat the process for each of the different types of wood.

Results

Range of Ballista (m) (±0.5 m)
	Mass of Projectile (g) (±0.5 g)
Trial	82	73	83	70	92
1	24.6	28.8	21	20.4	25.2
2	24.6	25.2	25.8	23.4	22.8
3	22.8	26.4	25.8	19.2	24.6
4	21.6	24	26.4	20.4	27.6
5	25.8	24	22.2	22.8	25.2
Mean	23.9	25.7	24.2	21.2	25.1
Standard Deviation	1.66	2.01	2.46	1.78	1.72

Data File: text .:. Excel

Calculations Used:

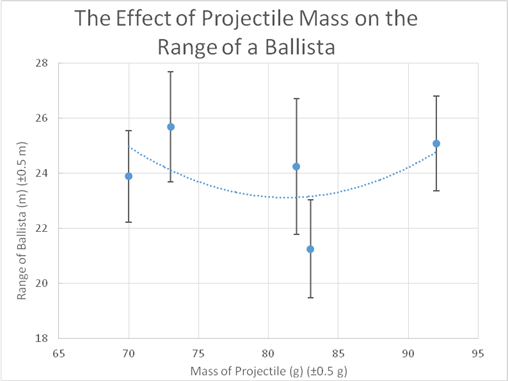
The data demonstrated that, to an extent, projectiles with both high and low masses tended to fly farther, and ones with medium masses didn’t fly quite as far.

Conclusion

From the data that was gathered during the experiment, it would appear that projectiles masses that were either relatively high or relatively low flew farther than there medium-mass counterparts. Prior to performing the inquiry, we believed that the distance travelled would be graphically be in a bell curve shape, with anything lighter or heavier than the optimum mass having less range. This hypothesis was not supported by the data from the experiment. In fact, the oak projectile, with a medium-weight of 83 g, had an average distance of 21.24 m. Whereas the walnut projectile, one of the lighter projectiles with a mass of 73 g, flew a mean distance of 25.68 m. This could be due to the reasons that were discussed in the background. Lighter projectiles are able to take advantage of the air current and float, leading to more time in the air and a longer distance overall. On the other hand, heavy projectiles have more momentum and are able to punch through the air in order to travel farther.

Although the lab was planned in order to minimize the potential for error, there were still some issues that could be addressed for future trials. Due to the space needed to perform the trials, the experiment had to be performed outside. This means that external forces like wind, temperature and atmospheric conditions may have had an effect on the final results. Plus, the use of a measuring wheel on uneven and grassy ground may have meant that some distance measurements weren’t entirely precise. The standard deviation values of our tests ranged from approximately 1.66 to 2.46. While the data was fairly accurate, the errors likely had an impact on the values that were recorded. This could be why the graphed data doesn’t necessarily follow a trend closely. To improve the procedure, a large, flat, indoor area would be a better location to perform the trials in as it would eliminate many external factors that could affect the results.

Bibliography

1. "Ballista." Ancientfortresses.org. Siteseen Ltd, n.d. Web. 13 Jan. 2015.

A explanation of Medieval castles and weaponry

2. "Ballista." Lords and Ladies.org. Siteseen Ltd, n.d. Web. 11 Jan. 2015.

A basic history of medieval warfare and weapons

3. Ancient Greek Artillery Technology

An article on the technology and weapons of Ancient Greece

4. Ballista

A page on the history and uses of the ballista

5. What Is a Ballista?

An explanation of the ballista as a siege weapon