Background Information
The principle of current dates back to the 1700s with Sir William Watson in England. He discovered that current could be sent through a wire in a circuit. It is believed that the current was from an electrostatic discharge, probably from a Leyden jar charged with high voltage. Long ago, people could create electric current by rubbing materials together such as glass and fur. Later on in 1800, Alessandro Volta described the parts of the early battery. It was made by layering silver, paper or cloth soaked in salt, and zinc. This was stacked until the desired voltage was reached. This is why we now call the potential through a battery or circuit “volts.” Then, by the end of the 19th century, the famous Thomas Edison created an alkaline battery, or cell, using iron as the anode material (-) and nickelic oxide as the cathode material (+). The electrolyte used was potassium hydroxide, which is the same used in modern alkaline batteries.
In this research paper, the capacity of these alkaline batteries will be tested against the capacity of the cell. The capacity of a battery is typically measured in amp-hours. An ampere is the measurement for electrical current and is defined as a coulomb of charge passing through an electrical conductor in one second. It is claimed that the battery capacity decreases as the rate of discharge increases. Because of this, many battery manufacturers prefer to rate their products at very low rates of discharge—they last much longer and therefore are rated higher on the market. This principle seems to work, if what you are trying to power is a small circuit, like a calculator. However, if the circuit you are trying to supply energy to requires a lot of current, a battery that can withstand a higher rate of discharge is needed. This led to the development of many different types of batteries and usages.
The typical drain of an alkaline AAA battery available at a local grocery store is 10mA. The capacity of the battery is typically 1000mAh under normal temperature (25°C or 77° F) and efficient discharge rate (usually 10-hour rate).
Purpose
The purpose of this investigation is to find the relationship, if any, between the discharge rate of AAA batteries, by manipulating the resistance in a circuit, and the capacity of the battery as measured in amp seconds.
Question
How is the capacity of a AAA battery affected by manipulating the resistance in the circuit, therefore changing the rate of discharge?
Hypothesis
The capacity, as measured in amp seconds, of a AAA battery will be higher with a low-rate discharge current than with a high-rate discharge current lasting for a shorter duration of time. This will occur because of the amount of heat lost and frictional losses from a high-rate discharge and a higher current of energy moving through the circuit, resulting in a less efficient circuit.
Set-up
For this experiment, there are a few variables that must be either known, or able to be calculated from the data taken in the process. These include: time in seconds (T), voltage in volts (V), resistance in ohms (R), current in amps (A), and, of course, capacity in amp seconds (C).
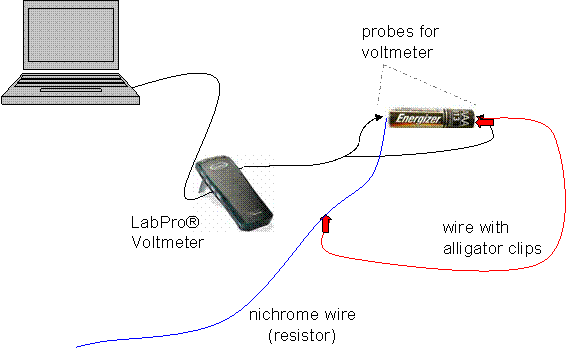
The first step was to build a simple series circuit with a AAA battery. I found a device to wrap around the battery in order to have something to fasten the wires to (a rubber band seemed to work just fine). Then, I connected a nichrome wire to the positive side of the battery; this wire is the resistor. From there, I attached a wire with alligator clips on each end, and vuala!, I made a working circuit.
In order to measure the voltage of the battery, a circuit must be connected to a voltmeter that will take consistent readings of the voltage across the battery until the power is completely dissipated. To make life easier, a LabPro® voltmeter can be connected to the positive and negative ends of the battery, and set up to a computer that will record the voltage across the battery twice per second until the battery essentially is drained.
Note: It was crucial that all wires were securely taped down—bumped wires altered the results!
Procedure
To change the discharge rate of the given battery, the resistance was manipulated. This is because the lower the resistance, the higher the current, and therefore, the faster the battery will discharge. In order to change the resistance, the alligator clip from the diagram above can be clipped to different positions along the length of the nichrome wire, adding resistance by increasing the length, and decreasing resistance by shortening the length of the nichrome wire in the circuit. In order to have enough data to find a trend, I performed 7 trials, beginning with 4cm length of nichrome wire and adding multiples of 4cm in length each trial (4cm, 8, 12, 16, 20, 24, 28). I hooked each battery up in the circuit, and let it drain all of its potential energy.
Data Collection and Calculations
Voltage
Remember, the voltage is a value that is known in this set-up, because the LabPro ® voltmeter recorded the potential twice per second until the battery dissipated. A table below shows the initial voltage across each battery for the seven different lengths of wire used.
Initial Voltage for Varying Lengths of Nichrome Wire
|
Length of nichrome wire (cm) |
Voltage (v) |
|
4 |
0.695971 |
|
8 |
0.876679 |
|
12 |
0.959707 |
|
16 |
0.964592 |
|
20 |
1.12576 |
|
24 |
1.24298 |
|
28 |
1.18437 |
As the length of the resistance wire increases, the potential also increases at a steady rate.
Resistance
In order to calculate the resistance in the circuit after each adjustment, I took a 2meter long segment of nichrome wire and used and ohmmeter. The longer the wire used to base the proportion off of, the more accurate the measurement. From this information, I simply set up a proportion to find the resistance of 1cm of wire and multiplied this by the length used in each trial. It was important that I kept as many significant figures as possible for accuracy.
Conversion Table of Length of Wire to Resistance
|
Length of nichrome wire (cm) |
Resistance (Ω) |
|
4 |
0.004651163 |
|
8 |
0.009302326 |
|
12 |
0.013953488 |
|
16 |
0.018604651 |
|
20 |
0.023255814 |
|
24 |
0.027906977 |
|
28 |
0.03255814 |
Time
Of course the time is a known variable in this experiment. Simply by looking at the data table of potentials that the computer recorded, the time it took to discharge the battery is the same time that the potential finally reached 0. However, since some of the batteries took over 8 hours to fully discharge, the time (in seconds) that it took each battery to discharge is recorded when the battery reaches a potential of 0.02 v. A data table below shows the relationship between the resistance and the time that the seven different batteries took to discharge to 0.02 v.
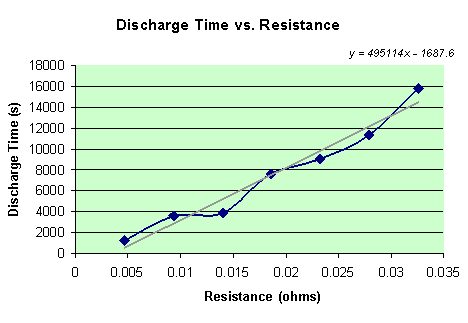
There is clearly a linear relationship in the data. As the resistance is increased, time is greatly increased. The equation for this line is y = 495114x – 1687.6.
Current
With both the potential and the resistance known, the current can be calculated with a simple formula: I = V/R. A data table below shows the initial currents of each trial.
Initial Current for Varying Lengths of Nichrome Wire
|
Length of nichrome wire (cm) |
Current (amps) |
|
4 |
149.63377 |
|
8 |
94.242993 |
|
12 |
68.779002 |
|
16 |
51.84682 |
|
20 |
48.40768 |
|
24 |
44.540117 |
|
28 |
36.377079 |
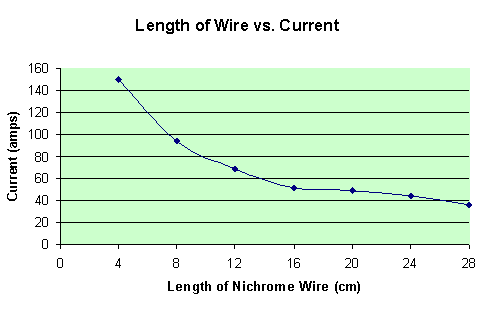
By looking at the graph above, there is an obvious, (and expected), trend in the data. As the length of wire increases, therefore increasing resistance in the simple circuit, the current must decrease. This all relates back to the wonderful equation I = V/R.
Capacity
Finally, what you’ve been waiting for… the capacity of the AAA battery in each of the seven different circuits! To find the capacity, as measuring in amp seconds, the total current must be found. Since data points were collected twice per second, all of the currents can be summed and multiplied by 0.5 to get the total current running through the battery. A graph of the capacities of each battery compared with the discharge rate, or seconds it took for the battery to drain, is displayed below.
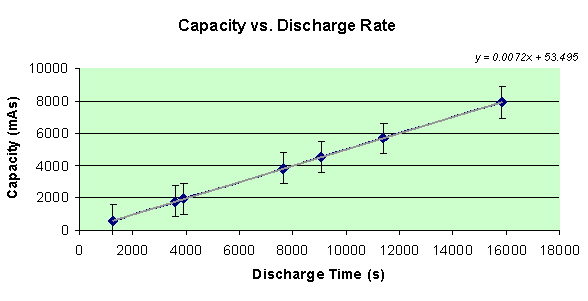
By looking at the graph, my hypothesis was correct in that when the battery takes longer to discharge its energy potential, the capacity of the battery is increased greatly. In fact, there is a very linear relationship between these two variables. The equation of the line is y = 0.0072x + 53.405.
Click on the links below to view the complete data spreadsheets. The files are divided up between different lengths of nichrome wire for the different resistances.
Restatement of Hypothesis
The capacity, as measured in amp seconds, of a AAA battery will be higher with a low-rate discharge current than with a high-rate discharge current lasting for a shorter duration of time. This will occur because of the amount of heat lost and frictional losses from a high-rate discharge and a higher current of energy moving through the circuit, resulting in a less efficient circuit.
Findings
Through this demonstration my hypothesis of the relationship between rate of discharge and capacity was proved to be correct. It is very evident, based upon the data collected and the calculations above that, when the discharge rate is increased by increasing the resistance in the circuit, the capacity of the battery is also increased at a linear rate of change defined as y = 0.0072x + 53.405. There is a strong enough trend to know that this is a valid relationship. This means that a AAA battery is most efficient in its energy output when it is discharged a low rate, with a low current running through the simple circuit (such as 36 amps running through a length of 28 cm of nichrome wire). When there is a high load across the battery, there are internal energy losses, frictional losses, and a release of energy in the form of heat at high currents. It would be an interesting investigation to test this same experiment in a parallel circuit and see how the type of circuit affects this relationship and if the results would be similar or not.
Another factor to examine is the actual graph of the potential vs. time as the battery discharges at different rates. The curve of 4cm of wire is compared with 28cm of wire below:
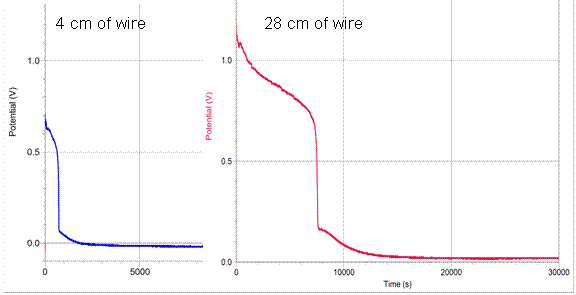
As shown, the curve is relatively similar in shape; however the 4cm length of resistance discharges much more rapidly than that of the 28cm wire. Additionally, both batteries discharge the last 0.05 v at a very slow rate. Other research has been done, and the last 0.05 v seem to disregard this length of time and potential. This is probably because it is a similar rate of discharge once it reaches that small of a potential.
Sources of Error
In terms of design set-up and methodology, the experiment seemed to keep controls consistent and accurate. However, since the batteries took anywhere from 0.5 hours to over 8 hours to discharge, sometimes another student could accidentally bump a wire in that lengthy window of time. For the most part, the set-up remained largely undisturbed. In addition, the width of the alligator clipped to the resistor was a factor affecting the precision of the length. Aware of this, I tried to measure from the end of the clip to the positive end of the battery, keeping consistency. Certainly more trials would produce more accurate and valid results. However, from the graph of the capacities, it is evident that there is a clear trend. To fully determine the relationship between discharge rate and capacity, larger lengths of wire for resistance should be tested to see if it continues to be a liner relationship, or if the line plateaus at some discharge rate, and no longer increases in capacity.
“History of Battery Invention and Development” <www.AllAboutBatteries.com> 2004.
“Notes on Batteries: Duration under Load” W.E. Johns <www.gizmology.net/batteries> 2003.
“Battery Capacity” Charles Wenzel <www.techlib.com> 1995-2007.
“Capacity and Battery Ratings” Engineers Edge <www.engineersedge.com/battery> 2000-2009.
“Battery Life” Monty Smith and Paul Wilson <www.climber.org> 2005.
This site contains a timeline of major developments in the history of the
battery cell, beginning with Benjamin Franklin in 1748 coining the term
"battery" to describe an array of charged glass plates.
Visit this site to read about battery life as well as how to determine which
would be the best battery to purchase for optimal usage in certain devices.
This site contains a tutorial called "Batteries 101: How Batteries Work" that
explains in detail how common disposable and rechargeable batteries function.
This site also provides valuable information about the care of batteries and an
interactive timeline of the history of the battery cell.
For information about factors that affect the life of a battery and its
capacity, such as temperature and pressure, visit this site. It includes
helpful graphs and explanations of the aging process of batteries.
Battery Capacity Conversion Often battery capacity is measured in milliamp-hours (mAh), however some companies choose to note different measurements of their product's capacity. This site contains helpful conversions for various measurements.
This site helps to define many of the terms used throughout this investigation
such as capacity and ampere-hours. There is also a conversion equation to
determine capacity versus discharge rate.