Before there were guns to fight wars, catapults and trebuchets used to be essential if an army wanted to achieve a victory. The most common trebuchet consists of a long pivoting beam, a very heavy counterweight swinging from a hinge at one end, and a sling with a big rock hooked to the other end. When released the weight drops, the beam rotates and the rock slides down the track in the sling. When free of the track the sling rotates very quickly up and over the beam, and slips off a hook. The rock goes out of the sling and flies away. The projectiles from these weapons had the potential of causing massive damage on any castles or barracks at which they were flung.[1] The more massive the rock, the more destructive the force would be. Of course this seems obvious when one takes into account Newton’s Second Law which states that force is equal to mass times acceleration (F=ma) which in this case is gravity. Early trebuchets were operated by hand, but as technology got better, they were flung with the help of gravity. These are what are called "counterweight trebuchets.”[2] Wheels were also put on these trebuchets to allow for more motion, mobility, and strength. These started to be used in the 1300’s and were kept in use all the way up to the 1500’s when advances in gunpowder exceeded the destructive force of trebuchets.[3]
Review of Literature
Most of the literature used talked about the time period trebuchets were in use, and how they were operated. This was good background knowledge, but it helped little in understanding the mechanics of the weapon which was the focus of the research. There was information found at seige-engine.com that did give designs of certain trebuchets, but not as much on how it worked.[4] By far the best information was found at the University of Carthage’s Physics Department web site because there was not only background information and in-depth trebuchet designs, but also an analysis of how these things worked.[5]
Research Question
If the mass of the counterweight or the the angle at which the projectile is launched is manipulated, how does it affect the distance a projectile travels?
Variables
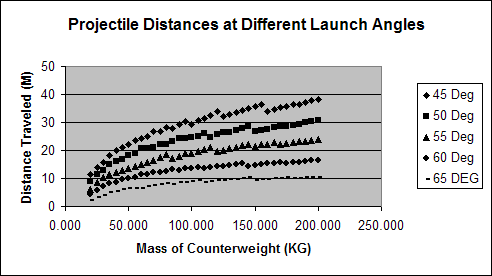
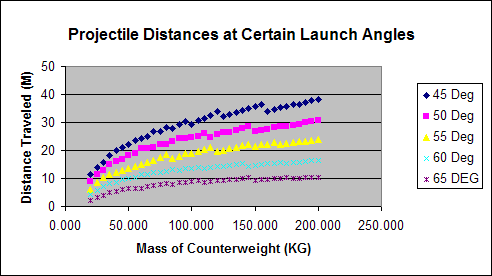
For the entire project, the distance that the projectile travels will be the dependent variable. There will be two different tests with two independent variables tested. The first independent variable is the mass of the counterweight with the angle of launch at a constant 45 degrees. The second independent variable is the angle at which the projectile is launched, and the mass of the counterweight will also change. For all tests, the mass of the projectile, the position of the fulcrum from the counterweight, and the couillard length will stay constant and air friction will be discounted as the tests will be run in a computer simulation on “Interactive Physics.”
Hypothesis
When the mass of the counterweight increases, the distance of the projectile will travel should increase in a linear path due to the relationship between gravity and the counterweight. As the force exerted on the projectile is equal to the mass of the counterweight times the gravitational constant, when the mass is increased, the force will also increase. Furthermore, because for every action there is an equal and opposite reaction (Newton’s Third Law), the force that is put on the counterweight should be the same force exerted on the projectile. The distance traveled then should be directly related to the mass of the counterweight. In the second test, the distance the projectile travels should be the greatest when the angle of release is closest to 45 degrees. This is due to the fact that there will be no air resistance on the projectile allowing 45 degrees to be the perfect arc for maximum distance.
Materials
For the purposes of this experiment, we have decided to utilize the technology that is available to us. We will be using the “Interactive Physics” program to simulate both the construction and launch of the trebuchet. Although it is theoretically possible to duplicate this experiment in perfect conditions, our research should be the most accurate because the “Interactive Physics” program allows us to negate the effects of air friction and it, in theory, carries out the mathematical formula to make a projection of where the mass should land. We will then be inputting all of our data into Microsoft Excel to ensure that we are able to most effectively evaluate the data.
Procedure
The Initial Design
Because we utilized the computer to carry out our experiment, we selected a program that would allow us to design a fairly complex model of a trebuchet, while maintaining a user friendly interface. The program “Interactive Physics” allowed us to create such a design. We began by making a simple catapult to experiment with the program’s capabilities and limitations. Although we would eventually encounter many problems with the program, it was initially very easy to use.
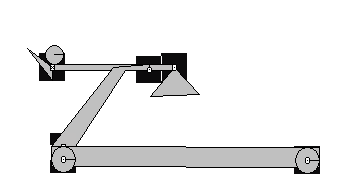
We slowly added parts to the catapult until it began to take the shape of a trebuchet (shown below). This design was too simple, however. Because of the structure of the couillard, we were unable to control the release mechanism and modify the release angle.
If you would like to view this model in real time and have "Interactive Physics" on your computer, click here. Although, as noted above, this version won't work very well.
The Final Setup
We eliminated the original design and replaced the couillard with something that looked more like this:
If you would like to view this model in real time and have "Interactive Physics" on your computer, click here. Again, as noted above, this is the model that we eneded up using. So it should work better.
By replacing the platform with the ball to rest on with a rigid joint, we could control when the projectile was released. Rather than letting physics dictate the angle of release, we could manipulate the joint to release in terms of the angle of the cross-beam. This allowed us to find the maximal release angle by modifying that angle between the range of 45°-65°.
Gettin’ To Work
Our experiment was relatively easy to carry out once we were able to create a working model of our trebuchet. Unfortunately, sitting in front of the computer for hours clicking the mouse repeatedly to collect roughly 185 data points gets old. Luckily, we were able to plan ahead and spread the work out over the semester to offset the effects of becoming overjoyed with physics.
To begin, we minimized the frame-rate to roughly one frame per .02 seconds and inserted a function into the computer that stopped the program once the projectile had crossed a certain plane on the y-axis. This functioned as both our “ground” and as a way to get an accurate measurement of the distance the ball had traveled. We launched the trebuchet with counterweights on a range of 20-200 kgs at 5 kg intervals. We then repeated this process for the 5 pre-selected angles.
The Experiment

Data Collection and Analysis