By Zach Peterson
- Design
- Method
- Results, Analysis, and Conclusions
- Raw Data
| top |
Scientists have been studying flames and microgravity separately for years, and the research is still incomplete and arguable. Fire, a force mankind has known of and used for millennia is loosely defined as “a chemical between two or more substances in which a large quantity of heat is involved,” (3) and we still don’t know how it really works. Microgravity, also known as 0-g, has only been studied for the past 35 years, only ever since the Apollo missions.
|
|
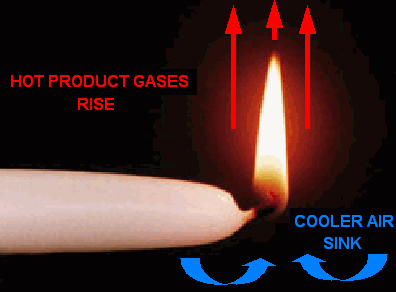
In contrast to what happens to flames on earth, in a zero-g environment, the glowing soot particles move away from the point of combustion at an equal speed and distance. Since there is no friction in a zero-g environment, then the flame appears spherical because of the pressure (created by the increase in heat at the point of combustion) that pushes the
|
Webster’s dictionary defines microgravity as a “condition in space of virtual absence of gravity.” So based on this, what exactly have I set out to do? After a bit of reading, I discovered that with the exception of being in orbit |
around the earth, the easiest way to replicate microgravity is with a fall. In a freefall, gravity has 1/100,000 the force it would on an object, essentially eliminating gravity from the equation (1,4,5). I suppose that the easiest way to test to see if you have really achieved microgravity is to place a candle inside the “microgravitic” space. Since we already know what happens to flames in microgravity, I chose to use this method to test whether or not I have achieved zero gravity.
| top |
Since we already know what happens to flames without gravity, this project turns from a cause and effect problem into an engineering problem. Since a candle would just go out if you drop it, then it needs to be shielded from rain, wind, etc. But after doing some more reading, and after remembering an important lesson from a chemistry class, fire needs oxygen. I had considered putting the candle inside a jar and closing the lid, but it needs oxygen to stay lit, or else it would burn out.
As stated above in the background information, I plan on testing whether or not I have achieved microgravity by watching a candle burn in a freefall. But obviously I can’t just drop a candle from a high place and expect it to stay lit, it needs to be in its own confined space. I suppose that microgravity can be achieved, and furthermore tested, by placing the candle in a clear container (a mason jar or something, but without the lid), and observing the flame. If the candle is really under the confines of microgravity, the flame will appear spherical.
| top |
My apparatus had to fit a few important requirements:
1) Reusable
2) Flame resistant
3) Confining (the flame has to be kept shielded from the environment)
4) Legal
The best way to meet these is with a mason jar or plastic container. A glass jar would fit all but the reusable requirement, and the plastic container would fit all but the flame resistant requirement. The only plastic container I had burned very easily and melted quickly, so I went with a mason jar. In order for it to be reusable, I had to find some way to keep it from breaking, and I didn’t want to have to buy six pickle jars and set them all up the same way.
Instead I bought five bungee cords, one measuring .644 m (2 feet) and the rest measuring .322 m (1 foot). First, I used a long alligator clip to put an old piece of chewing gum on the bottom of the jar, near the center (epoxy is hard to mix and I didn’t want to ruin my only alligator clip). Next, I took a candle and cut into it with a razor knife and exposed more of the wick. This way the flame would burn higher and brighter, and would melt the wax faster. I managed to get the candle to stick there, but later I decided to put a bit of super glue on the bottom of the candle. Next, I glued the top of the jar to the metal ring that wraps around the metal lid using some industrial strength epoxy glue, but I left the lid off so I could prod around if I needed to and to provide oxygen to the flame. I took the four bungee cords, and rammed them into the lid with a hammer at four equidistant points; then I hooked all four to the remaining cord. This created a pyramid that was reasonably stable.
|
Length: .31 m Bungee cord: .644 m Bungee cord pyramid Jar w/candle: .49 kg 12^2 – 1.5^2 = b^2 b=11.5 in. or .309 m |
The total length of the cords was .954 m. The total mass of the jar and candle weighed just over a pound, or .49 kg.
With this in mind, I thought next that based upon the work done upon the bungee cords, I would need to find the ultimate elongation of the bungee cords. Obviously it would be very hard to measure the elongation of the cords while in the fall, so I estimated, taking the mass of the apparatus into consideration first, 160% of the original length. This gives a total stretched length of 1.53 m, with a cord diameter of .006 m. The diameter is needed to calculate the force required to break the cord, as seen below:
Tensile properties of a ½ inch (.013 m) diameter bungee cord
|
Stretching properties |
Load (lbs. of force) |
Load (N) |
|
50% elongation |
5.5 |
24.5 |
|
75% |
8.25 |
36.8 |
|
100% |
11 |
49 |
|
125% |
13.8 |
61.5 |
|
Force needed to break |
280 |
1247.3 |
Using the following formula, I was able to calculate the final velocity, since I knew that the acceleration was 9.8 ms^-2, and the initial velocity was 0. At this point I decided to drop the jar from the roof of my dad’s shop, close to 13 m tall.
v^2=u^2+2as
v^2=(0^2)+2(9.8)(13)
v^2=254.8
v=15.96 m/s
This yields a final velocity of 15.96 m/s, or 36 mph. When the jar reaches the end of the cord’s stretchiness it begins to decelerate, and using the stretchiness of 160%, that gives a distance of 1.53 m.
v^2=u^2+2as
0^2=(15.96^2)+2(a)(1.53)
0=254.8+23.06a
-254.8=2.06a
a=-83.27 ms^-2
I was surprised when I first say this figure, but after thinking about the information, it made sense. Over a distance of .6 m, the jar has to decelerate in less than 1/40 of a second. I did a bit of math, and I figured that the deceleration would occur over a period of around .064 seconds. At this point I had figured out all the information I would need to conduct the experiment, so I decided to go for it.
| top |
I decided to perform three drops, including a fee tests to make sure it was safe. On the night of December 11, 2002, my dad climbed up on the roof of his shop and performed four drops. We did a few test drops to see how the apparatus would hold up, and it seemed okay. The first drop went well, the second time the jar had to be wiped out. The third time the candle fell over and the flame went out about half way down (but stayed lit), so I repeated it after putting another drop of glue on the bottom of the candle. The fourth time the jar separated from the lid and cords, and amazingly it stayed lit the whole time. Needless to say, the jar broke and I reasoned that maybe I should have used more glue. Aside from these few complications, my method was the same each time.
- Results, Analysis, and Conclusion
| top |
The results matched up with my hypothesis somewhat. The fact that the flame would appear spherical was true to a degree, but it looked like it was trailing a bit. This is probably because I left the lid off, allowing gravity’s convection currents to carry the soot particles upwards. On the other hand, I don’t see how I could have left the lid on, because the flame needs to have oxygen in order to continue to burn.
After I finished, and while I was typing this, I thought about how distances I was using. I could just have easily used a cord of around 5 m, which would elongate to maybe 8 m. That way my time measurements wouldn’t be decimals. I went back and did some rough calculations, and found that the time would have been maybe between 2 and 3 seconds. If I ever do another experiment like this, I would use longer cords and probably use an alcohol burner.
I suppose I could sum it up with a compare and contrast statement. In short, microgravity produces a round, cooler spherical flame. In one g (9.8 ms^-2), the flame appears conic, and the highest temperature is at the flame base. In microgravity, the highest temperature is at the flame “tip”, or the outermost point away from the point of combustion.
- Works Cited
| top |
1) Agosta, Vito. “Burning Velocity Measurement.” McGraw-Hill Encyclopedia of Science and Technology. Vol. 3. 8th Edition. McGraw-Hill. New York. 1997.
2) Giancoli, Douglas C. Physics: Principles with Applications. 3rd Edition. Prentice Hall. Englewood Cliffs, New Jersey. 1991.
3) International Baccalaureate: Physics Higher Level Data Booklet. Second Revised Edition. January 1998.
4) “Microgravity Combustion Science Brochure.” National Aeronautics and Space Administration. Accessed: 14:03 11.20.02
mgnwww.larc.nasa.gov/bd/combustion/combustion.gov
5) “Why Microgravity?” University of California Berkeley. Accessed: 16:18 11.21.02