Katie and Mary's Battle With
Simulacra!!!!

Cellular automata are “computer simulations that try to emulate the way the laws of nature are supposed to work in nature” (Ehrencrona). Cellular automata may not necessarily be completely accurate all of the time, but they do provide some answers as to how an organism reacts towards its environment. Cellular automata also may illustrate the ways certain diseases behave such as Cancer. Furthermore, the cellular automata is a community of cells which interact with one another. Thus, the cellular automata serves to depict both population and community ecology since it incorporates the interactions of different cells within a pattern. The cells behave in a way that depending on the location of one cell, a neighboring cell will either survive, become deactivated and “die,” or be born.
There are several essential features of cellular automaton. These include: its state, which can either be a number or a property; its neighborhood, which consists of the cells with which it interacts; and its program, which defines the changes that it endures in response to its status and that of its neighbors. The state, explained in biological terms, could represent “the number of animals at each location or the type of forest cover growing there…if each cell represents part of a landscape” (Green). Furthermore, the states could correspond to environmental features such as coral cover or topography. Cellular automata also possess several properties, which consist of self-organization, life-like behavior, and “thermal” behavior. In self-organization, patterns are forced to emerge. Furthermore, in life-like behavior, the automata behave in ways like those of biological systems. For example, the cells may: “die out, become stable or cycle with a fixed period, grow indefinitely at a fixed speed, or grow and contract irregularly” (Green). In thermal behavior, configurations may either be frozen into a stable pattern or may behave in a more active, gaseous way.
In cellular automata, several items can be altered. These include: the number of states per cell, the number of dimensions, the way cells are arranged, the neighborhood, the weight of neighbors, and the operations performed on neighbors (Wójtowicz). In addition, the parameters can be altered, the birth and survival rates changed, by selecting a different number that a cell requires to be born or to survive. Although the typical birth/survival numbers are 3, and 2 and 3, these numbers can be altered so that the birth/survival numbers could be 5, and 4 and 7.
The game of LIFE was invented by the mathematician John Conway. In this program, a cell is either alive or dead, and the effect of a cell’s neighbors’ location is determined as it is this that determines whether or not the cell is alive or dead. This is supposed to be reminiscent of population change. In this program the rules are:
1. A living cell with only 0 or 1 living neighbors dies from isolation.
2. A living cell with 4 or more living neighbors dies from overcrowding.
3. A dead cell with exactly 3 living neighbors becomes alive.
4. All other cells remain unchanged.
However, as mentioned above, these numbers may be altered. The standard is what we listed in 1-4, but by altering the parameters, we can adjust the birth/survival numbers to any number we want to. (The survival rate represents the number of neighbors a cell needs to survive, and the birth rate represents the number of neighbors for a cell to come to life.) As the generations pass, cells either are maintained in some type of order, broken up into isolated patterns, or disappear.
In the Life program, the number of states can be altered in addition to the survival and birth rates. Within my experiment, the state refers to the state of the cell. A cell with two states would be considered either “alive” or “dead.” A cell with 8 states would be either “dead” or seven shades of alive. In the case of our cellular automata viewer (CAV), the states are represented by different colors or different shades of color. To illustrate this, imagine the states representing the forest cover (and its different stages), and after examining the effects of a forest fire, the states could represent the different stages a forest progresses through including bare earth, grass, woodland, and closed forest.
Preston and Duff write, “ Conway. . . discovered a simple rule which had an immediate effect, i.e. led eventually to either a stable pattern or to patterns exhibiting a repetitive, i.e. oscillatory, stability” (10). Although it is evident that the different programs within the cellular automata viewer do emerge as patterns, whether stable or completely random, we would like to pursue the effects of altering a parameter, the number of states. We would like to see what effect this would have on the original pattern. Thus, we intend to manipulate the states to see if a cycle emerges in the population.
Statement of the Problem:
What will happen when the states of a pattern are altered in an environment where the birth and survival rates equal zero?
Statement of the Hypothesis: If we increase the number of states in a pattern, then it will cause an increase in the number of generations within a cycle.
We began by downloading the cellular automata viewer 2.0 CavGB from the site: http://www.rennard.org/alife/english/cavgb.html. Since we were fairly inexperienced with this program, we learned the basics of how to use it by using the help section and figuring out what all of the different devices in the main bar and the control panel represented. Out of the four available programs for cellular automata (Life, Vote, 1D Wolfram, and 1DB Langton), the Life mode seemed the most appealing. Next, we figured out how to alter the birth, survival, and state rates. We also learned how to change the dimensions (the size of the cells), the speed, whether or not it ran all at once or step by step, and how to save a pattern which we created.
We created my pattern by selecting a “random” scattering of data under dimension one (which zooms in on the cells). Once we had created our own pattern, and saved it as “JINX,” we then altered the birth, survival and state rates. We chose to select zero for both the birth and survival rates. Since we had set out to determine the effects of the states on the population, we kept the survival and birth rates at zero throughout the entire lab, but we changed the states. The states thus served as the independent variable which would alter the dependent variable, the population.
In the JINX pattern, we first found the population numbers for the first thirty generations after we altered the state number. Once the birth and survival rates were at zero, we began tracking data on Excel for the second state. Then we changed to the third state and tracked the next set of data. We continued to do this for each state. As soon as we had collected all of the data concerning each generation’s population under the seven different states, we then observed at what point the numbers in the population became a cyclic pattern. We then further analyzed what happened when the population did emerge as a repetitious cycle.
Since we wanted to have multiple trials, we decided to run three other trials, one of which we created. We ran the patterns: Oscillator 01, Acorn, and our creation, panda. We did the same thing with these three patterns as we did with JINX. However, with some of these patterns, we had to track the population numbers past the thirtieth generation because it took longer for a population to emerge as a cyclic pattern. Once the patterns did have repetitious cycles, we marked what these cycles were and what population numbers were contained within these cycles. Since the third state never proved to have a repetitious cycle, we continued to run it until the 600th generation. When we had all of my data compiled on to Excel, we then produced graphs to analyze and compare the data.
Overall, we observed the effect the alteration of the states had on the population. We wanted to see what would happen when we increased the states and whether or not it would take longer for the population to become cyclic.
Below is the data representing the population numbers at each generation for each different state. The numbers in bold signify where the repetitious cycle begins. The highlighted portions indicate the repetitious cycle.
JINX
(started out with an even population)
Here is a graph of JINX representing the data from the table above. Its periodic nature shows its cyclic nature. This periodic nature displays the life-like behavior of cellular automata.
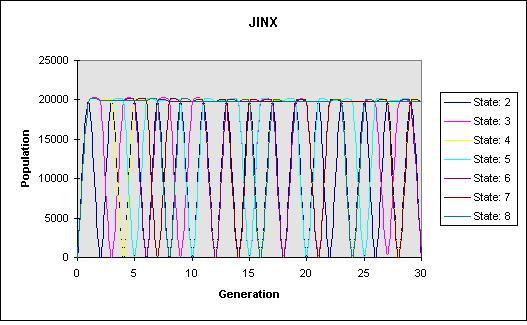
PANDA
(started out with odd population)
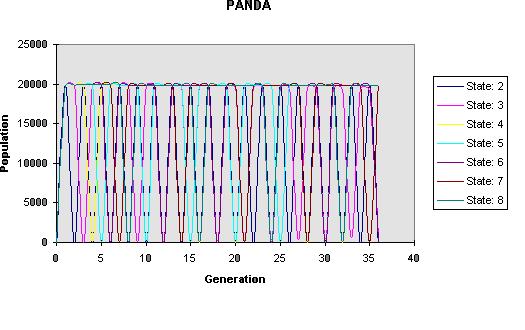
Oscillator 01
(started out with even population)
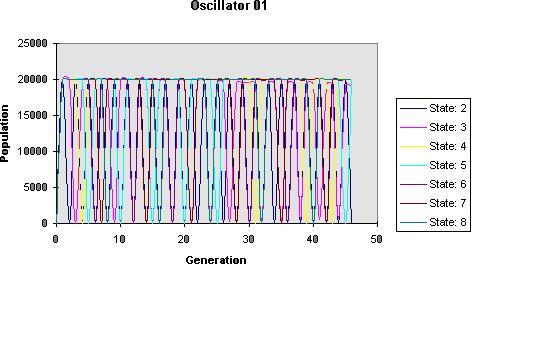
ACORN
(started out with odd population)
|
Generation
|
State: 2
|
State: 3
|
State: 4
|
State: 5
|
State: 6
|
State: 7
|
State: 8
|
|
0
|
7
|
7
|
7
|
7
|
7
|
7
|
7
|
|
1
|
19966
|
19972
|
19972
|
19972
|
19972
|
19972
|
19972
|
|
2
|
9
|
19968
|
19974
|
19974
|
19974
|
19974
|
19974
|
|
3
|
19966
|
19
|
19981
|
19987
|
19987
|
19987
|
19987
|
|
4
|
9
|
19960
|
18
|
19983
|
19989
|
19989
|
19989
|
|
5
|
19966
|
19946
|
19982
|
23
|
19984
|
19990
|
19990
|
|
6
|
9
|
41
|
19969
|
19985
|
24
|
19986
|
19992
|
|
7
|
19966
|
19943
|
19984
|
19975
|
19980
|
22
|
19986
|
|
8
|
9
|
19919
|
19
|
19981
|
19968
|
19978
|
22
|
|
9
|
19966
|
70
|
19986
|
19980
|
19973
|
19965
|
19978
|
|
10
|
9
|
19918
|
19969
|
20
|
19973
|
19966
|
19965
|
|
11
|
19966
|
19887
|
19986
|
19980
|
19970
|
19966
|
19966
|
|
12
|
9
|
109
|
19
|
19976
|
13
|
19966
|
19966
|
|
13
|
19966
|
19889
|
19986
|
19980
|
19971
|
19966
|
19966
|
|
14
|
9
|
19854
|
19969
|
19980
|
19964
|
8
|
19966
|
|
15
|
19966
|
154
|
19986
|
21
|
19967
|
19966
|
19966
|
|
16
|
9
|
19851
|
19
|
19980
|
19967
|
19963
|
8
|
|
17
|
19966
|
19822
|
19986
|
19976
|
19967
|
19966
|
19966
|
|
18
|
9
|
206
|
19969
|
19981
|
9
|
19966
|
19963
|
|
19
|
19966
|
19803
|
19986
|
19980
|
19967
|
19966
|
19966
|
|
20
|
9
|
19792
|
19
|
21
|
19964
|
19966
|
19966
|
|
21
|
19966
|
266
|
19986
|
19980
|
19967
|
8
|
19966
|
|
22
|
9
|
19745
|
19969
|
19976
|
19967
|
19966
|
19966
|
|
23
|
19966
|
19764
|
19986
|
19981
|
19967
|
19963
|
19966
|
|
24
|
9
|
336
|
19
|
19980
|
9
|
19966
|
8
|
|
25
|
19966
|
19679
|
19986
|
21
|
19967
|
19966
|
19966
|
|
26
|
9
|
19736
|
19969
|
19980
|
19964
|
19966
|
19963
|
|
27
|
19966
|
414
|
19986
|
19976
|
19967
|
19966
|
19966
|
|
28
|
9
|
19605
|
19
|
19981
|
19967
|
8
|
19966
|
|
29
|
19966
|
19708
|
19986
|
19980
|
19967
|
19966
|
19966
|
|
30
|
9
|
500
|
19969
|
21
|
9
|
19963
|
19966
|
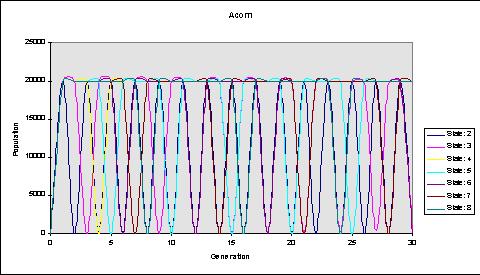
We realized for most of my patterns (JINX, Panda, Oscillator, and Acorn) the states two and four through eight were periodic in nature. Although they are periodic, it is evident that there are boom and bust cycles, with the boom occurring as the population increases, and the bust occurring as the population crashes and decreases. Overall, it is evident on the graph for states two and four through eight that there exists a carrying capacity at around 10,000. The population size oscillates around this number. Altering the states overall had no effect on the carrying capacity. When we altered the states, the carrying capacity continued to occur at around 10,000. The difference was that when the states increased, the population was maintained at a larger population for a longer period of time.
Overall, we saw that the number of states equaled the number of generations in a cycle (i.e. the fifth state had five generations within a cycle) except State 3 on all and the fourth state on JINX. State three graphs showed a regression of the maximums and minimums; therefore the graph decreased vertically in size. The trend eventually narrowed down to a range within the 5000s. Thus, the carrying capacity was around this number.
So, we analyzed the third state more closely. Since the behavior of the third state was the same for all four patterns, we decided a concentration on one would prove necessary. We decided to study JINX.
The graph below represents the population numbers which were low, and it focuses on what kind of cycle they are in. Based on the graph, at first it looks as if the numbers increase exponentially. We ran the pattern until around the 600th generation and found that the population averaged out around 5000-5300. Therefore, this graph would start out exponentially, but at a certain inflection point, it changes and becomes more logistic, reaching a limit. This would support the logistic growth of populations found in populations, where the population of an organism reaches some limit. This limit that the population is influenced by is the carrying capacity, the number of individuals the environment can support for a certain amount of time. Time, in this instance, is represented by the number of generations. The carrying capacity may be influenced by the food supply or access to sheltered sites (in animals), or access to sunlight or the availability of water (in plants). In the third state, it just so happens that the carrying capacity occurs at around 5000-5300.
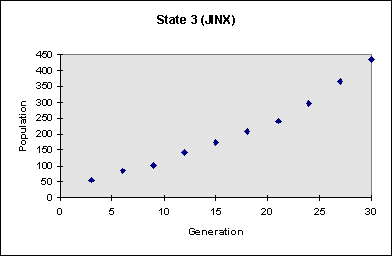
The following graph represents the high population figures within the same pattern JINX. Unlike the graph above, it decreases exponentially, and then at some inflection point (not represented on graph), the exponential graph evolves into a logistic graph, in which the population reaches some limit. However, in the following graph, it is different from the one above because unlike the one above, the graph does not increase until it reaches a carrying capacity. Instead, it decreases until it reaches a point where the population is henceforth stabilized between 5000 and 5300. This population is obviously influenced by the carrying capacity though, since it approaches a limit and the carrying capacity represents the limit where the population is maintained. So, even though the population numbers are decreasing, they are approaching a number that the environment can provide for, the carrying capacity. Thus, in both graphs, the curves started out exponential, but later emerged as logistic, showing that the population was influenced by the carrying capacity in the third state.
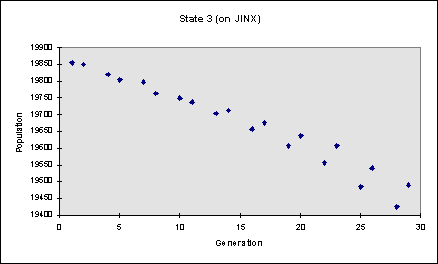
The following graph is an overall graph of the population numbers recorded from the 1434 to the 1490 generation. The graph shows that the graph oscillates around 5000-5300. Although the population numbers have changed drastically from the beginning thirty generations, Jinx has still retained the periodic cycle. It has merely evened out around a certain population (represented by this carrying capacity). Although the population still hasn’t emerged as a repetitious cycle (and it’s likely it never will), it does act as an oscillating pattern influenced by the carrying capacity.
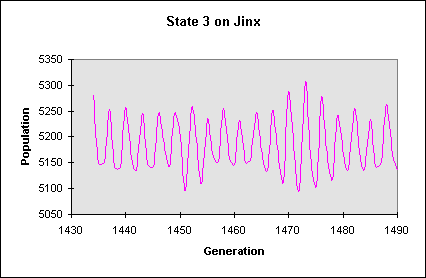
Overall, we did not encounter much uncertainty since the data we obtained came exactly from the cellular automata program. However, it is possible, that as we recorded the data into Excel, we accidentally entered inaccurate data. Also, CAV (cellular automata viewer) and cellular automata in general are relatively new, and there may be certain concepts that have yet to be discovered about the program.
Our data proved my hypothesis to be correct. In our hypothesis, we predicted that the number of generations in a repeating cycle would increase as we increased the number of states.
For example:
2nd state: 19831, 44
3rd state: never emerged as a repetitious cycle
4th state: 58, 19870, 19838, 19871
5th state: 19877, 19844, 19882, 19870, 79
6th state: 19831, 19848, 19850, 19848, 50, 19846
7th state: 19871, 19869, 19873, 19866, 66, 19865, 19845
8th state: 19871, 19869, 19873, 19873, 19866, 66, 19865, 19845
Not only did it increase, but the number of generations in a cycle equaled the number of states. This was evident in the above examples (taken from Panda’s data). All of this occurred in each trial (Panda, JINX, Acorn, Oscillator 1) except with three, and state four did not work in JINX. We do not know why three didn’t work, but it never emerged as a cyclic pattern. Although it did look periodic, it just wasn’t a repetitive cycle. In the third state, the low populations steadily increased and the high populations steadily decreased, so eventually, the population stabilized around 5000-5300. This occurred around the 600th generation. We could have made our lab more accurate by actually tracking the data points at these generations (from the first generation to the 1500 generation) and depicting this information on a graph, but that would have been over ambitious. Instead, we found it sufficient enough to graph the beginning thirty generations, and then the 1434-1490 generations, just to show what the population eventually looked like. We figured by just eyeing the population numbers at the 600th generation, we would have been led to the same conclusion. Also, we do not really know why state four did not work in JINX. However, state four wasn’t nearly as random as state three for although it did not follow the same pattern as the other states, it did operate around the same numbers, just not exactly. In states three and four, the populations did cycle in the same fashion, where the number of generations in the so-called pattern did equal the number of states; however, these numbers were not exact. And state three eventually led to a different population of 5000-5300, whereas state four basically stayed around the same population. Thus, although not all of our data supported our hypothesis, the vast majority of it did. An additional hypothesis that might have explained my data could have been that the number of generations within a repetitious cycle would equal the exact number of states which the pattern was in. In all of our population graphs, we were able to observe there being a carrying capacity that influenced the population. For states two and four through eight, this carrying capacity seemed to be around ten thousand, even though the graph wasn’t necessarily logistic. The graph was stationed around this carrying capacity and would increase or decrease, but it oscillated around this point. The graph of the third state also proved to have a carrying capacity, despite its randomness. After examining the high and low population numbers, we discovered that the graph eventually emerged as a logistic graph, with a carrying capacity of around 5000-5200. Overall, the graphs for state two and four through eight contained repetitious cycles, which are not truly common in actual life. Therefore, perhaps state three was a more accurate predictor of actual life patterns due to its randomness.
As was stated before, in life-like behavior, the automata behave in ways like those of biological systems. The cells may: “die out, become stable or cycle with a fixed period, grow indefinitely at a fixed speed, or grow and contract irregularly” (Green). Our data possessed this life-like behavior, characteristic of biological systems. In states two and four through eight the cells emerged as a pattern that became stable and cycled with a fixed period. Likewise, in state three, the cells grew and contracted irregularly, while at the same time, they eventually became stable. So even though this was a computer program, it was able to emulate what actually occurs in nature, the interaction between organisms (cells), and the effect of the states (environmental factors like topography) on their population. The program also produced populations whose populations were reminiscent of population trends that occur in nature, as well as populations that possessed carrying capacities, which are evident in nature.
Overall, our method was effective in producing the results we wanted. Some limitations we encountered were present in the actual cellular automata program we used. For instance, a limitation could have been the number of states that we could alter. We could only alter the states from two to eight. We do not know if there exists a program in which more states can be altered, but if such a program exists, it would have allowed us to study the effects of altering the states more extensively. Also, another limitation could have been that we only emphasized the importance of the states. We could have researched the effects of altering all of the parameters, including the birth and survival rate. Instead of having the birth and survival rate at zero all the time, we could have changed it to one for both the survival and birth rate. However, it would have taken years to analyze and compile all of the different combinations. Also, it might have been better if we had examined a different birth and survival rate since zero is a bizarre number to have as the birth and survival rate. Having zero as the birth and survival rate would mean that in order for a cell to survive, it must have zero neighbors, and for a cell to be reactivated, or born, it must have zero numbers. This combination would not occur in nature, since in order to survive, or “reproduce,” it is necessary to have neighbors. Thus, having zero has the birth and survival rates at zero could have been an unrealistic combination and one that is unrepresentative of what actually occurs in nature. It would almost be like spontaneous generation in a sense, since a cell would be born without needing any neighboring cells. Instead of cells reproducing, a cell would just suddenly appear out of nowhere, much like in spontaneous generation.
Also, we could have researched the other programs within the cellular automata viewer, which would have included vote mode, mode 1D (Wolfram), and mode 1DB (Langton). However, we knew beforehand that we wanted to research the life program because we would be able to alter the parameters more easily. Plus we did not have enough time to do a comprehensive study of everything in the cellular automata viewer. It was realistic to emphasize a quality about a particular mode, and go in depth about the effects that quality has on the mode. This was exactly what we did: we specifically studied the life mode, and researched the effects of altering the states. Since we always had the birth and survival rates at zero, we were able to do an in-depth study of one environment. Also, we could always have done more patterns, but we found that four patterns were sufficient enough. Also, we could have collected more data points for each pattern, especially for the third state. Since we stopped at around thirty to forty generations, we never closely examined what the population size was at the 600th generation. We did, however, run it, and we made assumptions about what eventually occurred. If we wanted to make an improvement, we could have collected population numbers for the third sate when it’s generation number was really high (continued after the 1500 generation). We could have done this for the third state in each pattern (Jinx, panda, Oscillator 01, and Acorn ). Instead of analyzing all the pattern’s third state, we just examined Jinx’s. We had noticed that the third states had behaved pretty uniformly; however, there could have been subtle differences that might have altered our conclusions about the third sate. Thus, we could have gone more in depth on the third state for all four patterns, instead of just one.
Ehrencrona,
Andreas. Cellular Automata. 28 Oct 2002 <http://cgi.student.nada.kth.se/cgi-bin/d95-aeh/get/lifeeng>.
Evolving
Cellular Automata. 2000. EvCA Group. 28 Oct 2002 <http://www.santafe.edu/projects/evca/>.
Green,
David G. Cellular Automata. 1993. Charles Sturt University. 28 Oct
2002 <http://life.csu.edu.au/complex/tutorials/tutorial1.html>.
Preston,
Kendall Jr., and Michael J.B. Duff. Modern Cellular Automata: Theory and
Applications. New York: Plenum Press, 1984.
Wojtowicz, Mirek, ed. What is Life and Cellular Automata?. 07 Jan 2002. Mcell. 29 Oct 2002
<http://psoup.math.wisc.edu/mcell/whatis_life.html>.
Wolfram, Stephen. Cellular Automata and Complexity: Collected Papers. 2002. Stephen Wolfram, LLC. 28 Oct 2002
<http://www.stephenwolfram.com/publications/books/ca-reprint/>.
Wolfram, Stephen. Theory and Applications of Cellular Automata (including selected papers 1983-1986). Singapore: World Scientific
Publishing, 1986.
Primarily, we used Rennard.org’s web pages on
cellular automata. We downloaded the CAV from the site; the author,
Jean-Philippe Renard, Ph. D. created it. Site:http://www.rennard.org/alife/english/acgh
Papers from Stephen Wolfram were also helpful in understanding the basics of cellular automata. Dr. Wolfram was a pioneer in the understanding of cellular automata. His book, A New Kind of Science, was recently released for further information.
Site: http://www.stephanwolfram.com/publications/article/ca/
Cellular Automata: Digital worlds provided a step-by-step method of explaining the essential components of cellular automata.
Site: http://www.ifs.tuwien.ac.at/~aschatt/info/ca/ca.html
Of course, we only explored the life program of the cellular automata viewer. Yet, cellular automata are also depicted within various programs. The history of the cellular automaton is included within this website.
Site: http://www.brunel.ac.uk/depts/AI/alife/al-ca.htm
This source was effective in explaining the basics of cellular automata, how the states work, and what determines whether or not the cell is alive or dead.
Site: http://psoup.math.wisc.edu/mcell/whatis_life.html
 +
+  +
+  =
= 
Note: Elephant picture from http://www.art.com/asp/sp.asp?PD=10054494&RFID=642275
Penguin mating pictures were from Guillaume Dargaud (site: http://www.gdargaud.net/Photo/ArchiveEmperor.html )If any qualms result from these pictures, keep in mind that our project looked at population growth, hence the mating.
Emperor penguin chick was from SeaWorld/Busch
Gardens Animal Information Database (site: http://www.seaworld.org/infobooks/Penguins/hatching.html
)