 Evan and
Tegan's Totally Awesome Physics Research page!
Evan and
Tegan's Totally Awesome Physics Research page!

This page is presented in glorious black background and white text to make it less abrasive to your eyes as you read. We are very concerned about your personal comfort as you read our page, and we feel that you will enjoy what we have to say even more if you are at ease while you are here.


Table of Contents
| Introduction | Materials/Procedure | Planning | Results | Conclusion | Bibliography | Related Links | Return to Research Page |
According to thermodynamics, when an
object is heated it causes the velocity of the molecules to increase. As the
velocity of the molecules increases the rate at which the molecules hit the
walls of the object also increases. This results in an increase in the force of
impact on the walls and causes the walls to be pushed out and therefore causes
an increase in the volume of the object itself. Likewise, when metal is cooled
down, the molecular velocity decreases and the force of impact on the walls is
lessened, allowing for a compaction of volume. The research question now
becomes, what effect does the increase in volume of the spring’s coils have on
the spring constant itself? When assessing this question, two potential frames
of reasoning come to mind. One may assume that because the spring volume is
increasing and typically thicker springs typically hold more weight, or have a
higher spring constant, the expansion in volume would allot for an increase in
the spring constant. However, the opposing idea would be that because the
matter of the spring is not increased, simply the volume, the spring would
actually become weaker because the molecules are no longer as tightly packed. However,
the focus of our research is simply to see whether an effect is present, not
why it is or is not. Based upon research, it is our hypothesis that by
increasing the temperature of a steel spring, the increase of volume of the
spring will lead to a decrease in the spring constant. Support for this idea is
as follows,
“Most objects expand when they are heated
and contract when they are cooled. Most objects also get hotter when they are
compressed and cooler when they are expanded. This effect can get complicated
because the values of the elastic module also depend on temperature, usually
getting smaller for higher temperatures” (2000 Oxford Dictionary of Physics).
This
means that as the
temperature increases, the spring constant decreases and a visible weakening of
the spring should be noted.
As far as
accounting for potential room for error there are three main areas that must be
taken into consideration. The first of these is the ability of the spring to
resist deformation. The atomic volume of steel is said to increase
exponentially with its temperature. While
the increase is relatively small, particularly when considering an increase of
almost 2000 Kelvins is required to increase the atomic volume by 1e-3 mm3,
it is still enough to cause a significant change in the ability of the spring
to resist deformation. However, to avoid
this, temperatures will be kept well under 2000 Kelvins.
The second
of these is the possibility of the spring becoming plastically deformed.
Hooke’s Law states that stress is linearly proportional to strain. If the stress is doubled then the strain is
doubled; if the stress is tripled than the strain increases threefold. However, there are limitations to the
validity of Hooke’s Law; it is usually only valid “for strains of far less than
1 percent. In most pure metals, for
example, the elastic limit is reached for strains as small as .001
percent. For larger strains, the object
never reverts exactly to its original shape on removal of the stress but
remains changed to some extent; it is said to be plastically deformed” (1996
Macmillian Encyclopedia of Physics).
The third
potential room for error is creep. “Creep is the term used to describe the
time-dependent plastic flow under conditions of constant load or stress. Whilst creep can occur over the whole
temperature range…with engineering metals and alloys, creep is of practical
importance only at high temperatures” (1972 Creep of Metals at High
Temperatures). However, high
temperatures typically pertain to those close to the melting point of the given
metal, and in this case the temperature to which the steel spring will be
heated will not be within range of its melting point.
Materials: one steel spring, ammeter, power supply, leads A and B,
stand, clamp, paperclip, mass holder (50 grams), and masses (grams).
Procedure:
1)
Locate a stand to suspend the spring
from. The stand should be about ten times longer than the spring (at least).
2)
Attach a clamp to the stand to
suspend the spring from. Make sure that the clamp is at least 5 inches away
from the stand itself so that no contact between the spring and the stand is
made.
3)
Locate a spring to be used. The
spring should have a loop at the top of it perpendicular to the rest of the
coils to allow it to be hung.
4)
Attach the spring so that it is
dangling from the clamp. The spring should form a 90-degree angle with the
clamp and be parallel to the stand. The spring should be hanging straight with
no curve in it.
5)
Hook the ammeter up the power supply.
6)
Attach lead A to the top spring loop;
secure lead B to the bottom spring coil.
7)
Take a paper clip and bend it into a
crescent shape and suspend it from the bottom spring coil.
8)
Attach the mass holder to the paper
clip (the mass holder should be equal to 50 grams).
9)
Run the experiment with approximately
each of the following amounts of current: 0A, 1A, and 3A. For each current use
masses of 50, 100, 150, and 200 grams to stretch the string. Remember that the
mass holder itself has a mass of 50 grams and use only it for the 50 grams
mass. Then add a 50 grams mass to the mass holder for a total of 100 grams and
so on. Record results.
The procedure above was the one used in actually when running
our lab, however, it was not the original one planned. While actually running
our lab we had to account for certain aspects, which in turn required an
alteration to our original procedure. The first of these would be that it was
anticipated we would be able to use actual temperature calculations to mark the
decrease in the spring constant. However, it became increasing difficult to
find a way to heat the spring in the first place. We originally had planned to
heat the spring in water and use a thermometer to get the temperature of the
water and then assume that temperature would equal the temperature of the
spring because we would allow it to remain submerged for some time. However, we
decided this would leave too much room for error because the container the
water was heated in would have to be exposed to some source of heat, obviously,
and we knew that the spring would sink to the bottom of the container and come
in direct contact with the container. This would potentially cause the spring
to be laid up against the part of the container being heated and the heat
source would cause the container to be hotter in that spot then that actual
over all temperature of the water. However, because we would be relying on the
temperature reading of the water and not the temperature of the actual
container directly above the heat source, we would have an inaccurate
temperature reading. Also, it would take a lot of time to heat each spring and
water to different temperatures and we could not be certain as to how long the
spring would need to be submerged before taking on the temperature of the water
in the first place. Instead we decided to run current through the spring, which
would cause an increase in the spring temperature, and use qualitative data. We
found that the increase in current caused a notable change in temperature
simply by touching the spring and therefore could tell the current was having the
desired effect on our spring. We also made sure that we attached connector
cables A and B directly to the endpoints of the spring. This was done out of
fear that attaching the connector cables anywhere other than directly to the
spring would cause a discrepancy between the actual amount of current running
through the spring and the reading of the ammeter because it would not be
running only through the spring but through other apparatus.
 1
1
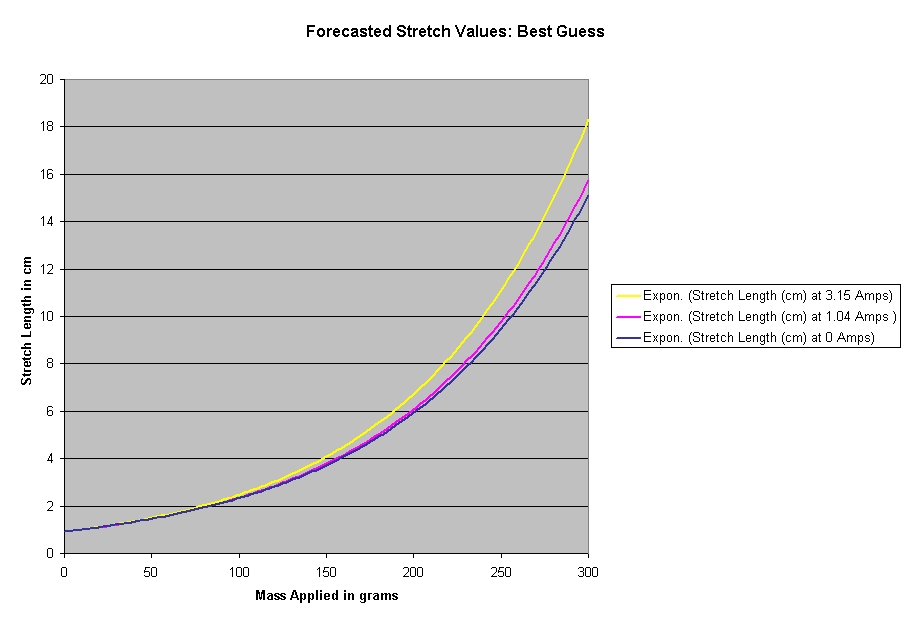
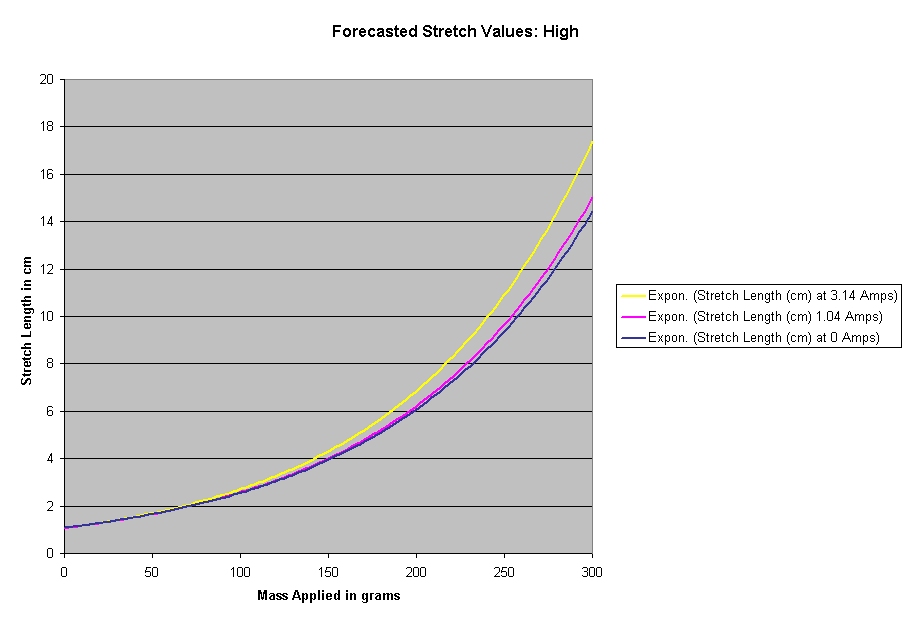
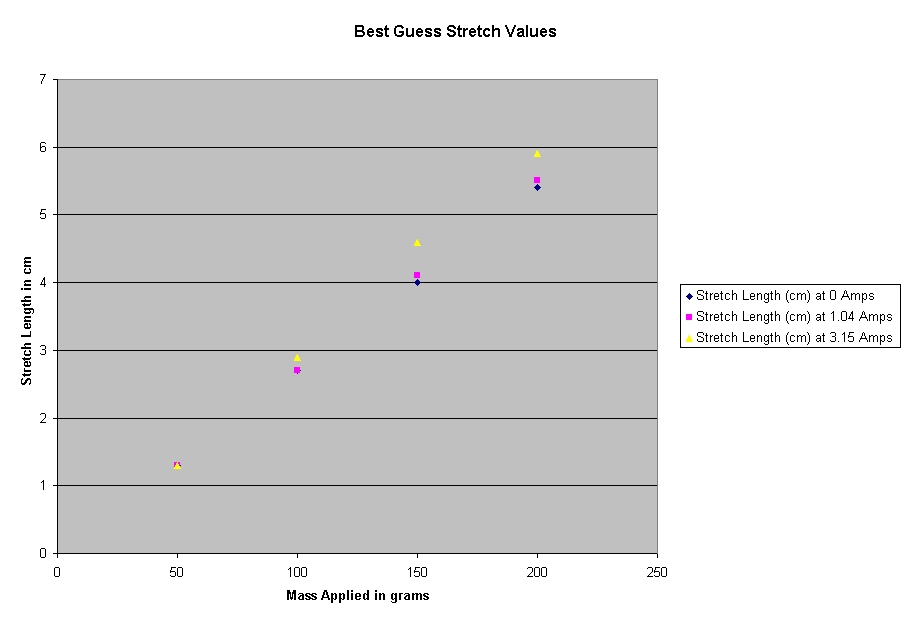
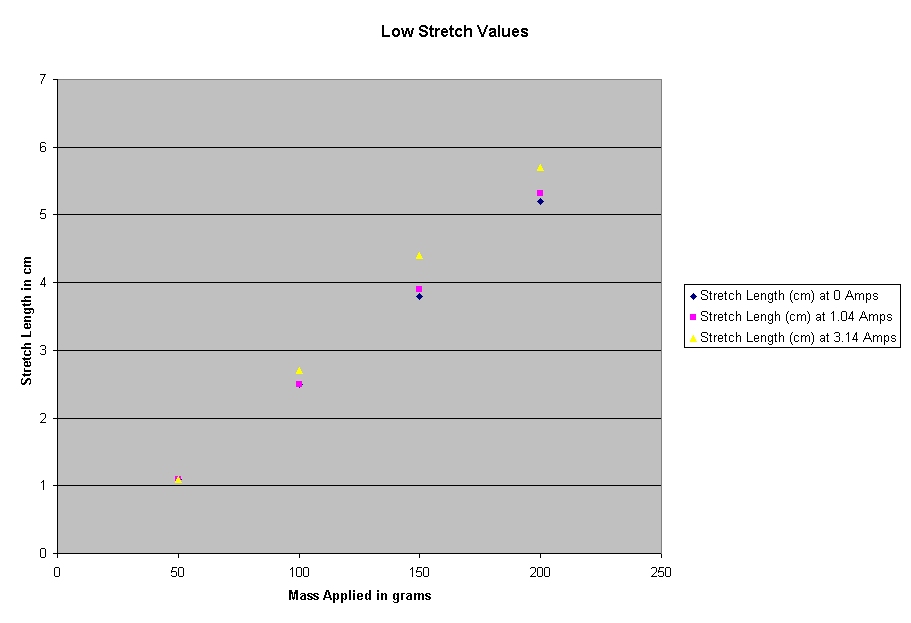
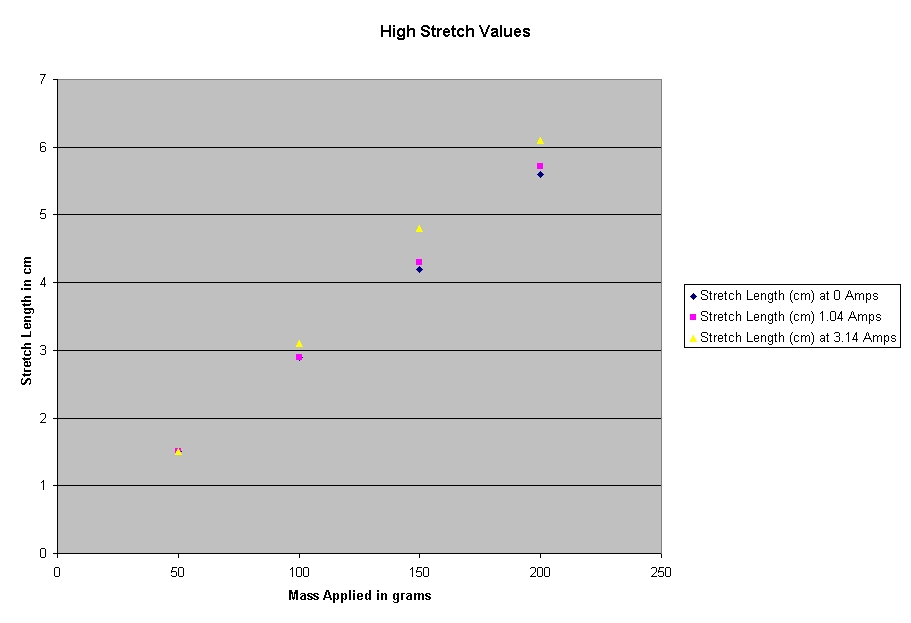
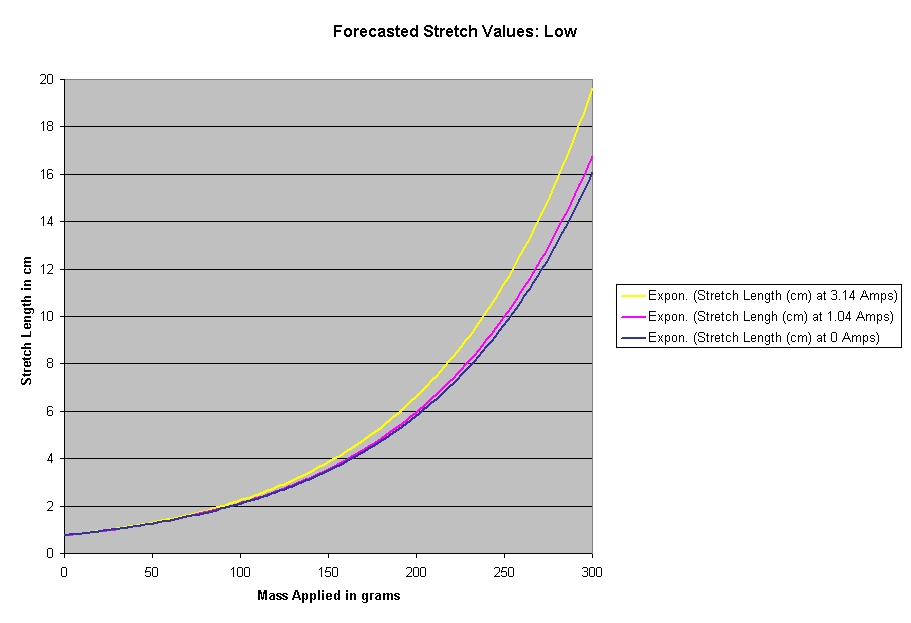
We have calculated an exponential growth for the amount that
each spring stretches with the amount of mass on it for each current. Of
greater significance, however, is that the exponential growth is shown to
increase with the increase of temperature.
Please also note these graphs.
We have concluded
that the spring constant decreases and the exponential growth of the amount of
length stretch increases with the increase in temperature. This is important to
the field of science for multiple reasons. The first of these is that in the
field of mechanical engineering, springs are often used in machines. However,
when work is done by machines, it is usually accompanied by the transformation
of energy into heat energy. This would cause an increase in temperature to the
machine and therefore an effect of the machine’s performance. The decrease in
the spring constant of the machine could lead to dangerous malfunctions and a
decrease of productivity. This information is helpful to mechanical engineers
so they can account for this problem and devise some form of cooling device for
the machines to insure proper functioning.
Furthermore, it could be possible that experiments run in different
environments could lead to a discrepancy in results. For example, an experiment
run outdoors in
Within our data there
are two possible areas where potential error occurred. The first of these is
that during testing, we did not check to see whether the spring, upon removal
of the mass, had reverted back to its previous form. In other words, we did not
check between the masses to make sure the spring had not become plastically
deformed and stretched to a longer length. This could generate room for error
because the amount of length stretched with each mass applied would have been
calculated incorrectly because we subtracted the original length of the spring,
6.5 cm, from the length with mass applied and if the spring did not revert back
to the 6.5 cm then the stretch distance would actually be less than calculated.
To avoid this in the future, it is recommended that the spring length be
measured between each application of mass and then that length be used to
subtract from the corresponding length measurement to calculate the stretch
distance.
The second potential room for error occurred during testing because when
we ran the current of 3.15 Amps through the spring and applied 200 grams mass
to it, upon removal the spring was plastically deformed. For all practical
purposes, the spring remained at the same length it had stretched to while the
mass was applied. Due to this we had to stop testing because our materials
could no longer be used. In retrospect, it would have been better if we had
been able to continue research and get more data to support our hypothesis.
Although we feel we have sufficient data to accept our hypothesis, more would
have been preferred. The lack of data that the deformation resulted in could
lead to room for error because not enough testing was done. Also, the fact that
after the 3.15 Amps the spring was plastically deformed, supports the previous
concern that the spring length should have been measured between each stretch
with mass to ensure we were subtracting the correct length. For the future, we
would recommend that a stronger spring be used and the current be increased in
smaller increments. The stronger spring would allow a higher current to be
reached before becoming plastically deformed and the smaller increments of
increase would allow for the collection of more data.
Although potential room for errors should be taken into consideration when
choosing to either accept or reject our hypothesis, we still feel that we are
able to accept our hypothesis for the following reasons. In reference to the
possibility of the spring becoming plastically deformed during testing and not
reverting back to its original length, we feel that if any permanent stretch
had occurred that was significant enough to really alter our results, it would
have been visibly noticeable and caused us to stop our experiment. Therefore,
if any plastic deformity occurred during testing it was not significant enough
to cause a large miscalculation in data and we feel that because of this our
data is reliable enough to accept our hypothesis. Furthermore, regarding our
having to stop testing prematurely, we still feel that even though only three
current readings were used, because we can notice a marked increase in
exponential growth based upon those three, it is enough to be able to
generalize that had we proceeded to use an increase in current and gain more
data, we would have seen the same marked increase that was visible from the
three exponential equations we were able to originally generate. Therefore,
although we would have preferred more data, it has not handicapped our ability
to accept our hypothesis.
Cook,
J Gordon. Creep of Metals at High
Temperatures.
Isaacs,
Alan. “Elastic Modulus.”
Meiners,
Harry F. Physics Demonstration
Experiments, 1970 ed.
Ridgen,
John S. “Elasticity,” “Elastic Moduli
and Constants.” Macmillan Encyclopedia of Physics, 1996 ed.
Trigg,
George L. “Steel.” Encyclopedia of Applied Physics, 1997
ed.