Uncertainty

     We encountered many errors in collecting our data. First, we were not able to use an electric mass, which makes our data not as accurate as possible. One big problem with using the manual mass was the factor of wind. The wind would always push the platform on the mass up or down, which could have greatly hindered the data, especially because the items being massed were only about twenty grams. The wind could create enough force to counter the force of gravity that the tuna can with water created. To try to solve the wind problem, we attempted to make a barrier in front of the mass, which helped, but did not work fully. We attempted, though, to make the data as accurate as possible, so when actually massing the cans, we made sure to do it when the wind was least present. When it was, however we made sure that the scale was as stable as possible, so we believe that the wind was not enough of a factor to hinder the data completely, although in our data there were some data points that came out not as we expected, for example the eighth data point, which was higher than the seventh. The wind might have been the reason for this, but there were other errors possible.

     Another error was that we had to drop the water balloons onto a dirt surface, which had small pebbles covering it. When the balloons hit, therefore, not only water splashed, but dirt and rocks too. This could have hindered our data in two ways. First off, some of the dirt and rocks that was splashed landed in the tuna cans collecting data. We did not take this into account prior to the experiment. We took out most of the rocks out of the cans, but we did not attempt to get the smaller ones, which would take some of the water out with the rocks. The dirt was impossible to remove because it instantly dissolved to make muddy water in the cans. Also, because the balloons landed on the rocks, the balloons might have popped on some sharp rocks, which could force the water splashing out of the balloon in separate directions than normal. Having the rocks in the splash area also made it not a flat surface, although it was very close, but that could have contributed to some false data points. In trying to solve this, we did put plastic bags on top of the dirt and rocks. This helped quite a bit, and only the existing tocks in the cans were in.

     We also thought that there could be a problem with the balloons. Some of them appeared weaker than others. Also, some balloons were weak on one side, but stronger on the other. This would also hinder the normal splash direction of the water. So that is a potential problem, but there is no way of making balloons perfect in any way, so we felt that this error probably had the least effect on the data. There was also another definite problem. Because the balloons were dropped one right after the other, a pool began to form eventually at the point of impact. That means that when the balloon would splash, the force caused by it would send existing water on the ground into the tuna cans. This was probably the most prominent factor that could hinder our data, along with the rocks. We could not figure out how to get rid of the pool, however. No matter where the balloons would be dropped, a pool would form. Also with this pool, it made the soil around the splash area very soft, and then the balloons being dropped would use some of their force to push on the ground, which created a little dip in the ground after we had concluded the collection of our data. This created another problem. One thing that we made sure of when we started the experiment was to have the splash area as high as the top of the tuna cans, so that the water collected in the cans did not have anything to do with the angle trajectory that the water was splashed out of the balloon with. If the water was ejected at a very low angle, it might run into the side of the tuna can. We wanted to retrieve as much water in the cans as possible, and the dip in the splash zone did not help, it just lowered the elevation of the splash zone. The last problem that we saw was basic human error. We had to manually scale each item, so the mass is not as accurate as possible. We also had to drop the balloons manually, so they were not exactly in the same spot every time. We were sure, however, to get all the balloons within a 6 to 10 inch area, as to create the least amount of false data. The plastic bags also helped this a little, but no matter what a pool would form, we are not sure how to solve that.

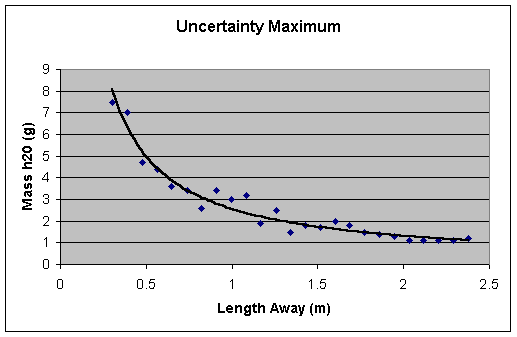
     Because of these errors uncertainty in the data was definitely needed. For the uncertainty, I took into account all of the possible factors that would contribute to faulty data, and thought that the uncertainty be plus or minus one gram for each tuna can. This would make the data for the maximum amount as follows:

uncertainty max (g)	length away (m)
7.5	0.305
7.0	0.39
4.7	0.479
4.4	0.564
3.6	0.649
3.4	0.738
2.6	0.823
3.4	0.908
3.0	0.997
3.2	1.082
1.9	1.167
2.5	1.256
1.5	1.341
1.8	1.426
1.7	1.515
2.0	1.6
1.8	1.686
1.5	1.774
1.4	1.859
1.3	1.945
1.1	2.033
1.1	2.118
1.1	2.204
1.1	2.292
1.2	2.377

uncertainty min (g)	length away (m)
5.5	0.305
5.0	0.39
2.7	0.479
2.4	0.564
1.6	0.649
1.4	0.738
0.6	0.823
1.4	0.908
1.0	0.997
1.2	1.082
-0.1	1.167
0.5	1.256
-0.5	1.341
-0.2	1.426
-0.3	1.515
0.0	1.6
-0.2	1.686
-0.5	1.774
-0.6	1.859
-0.7	1.945
-0.9	2.033
-0.9	2.118
-0.9	2.204
-0.9	2.292
-0.8	2.377

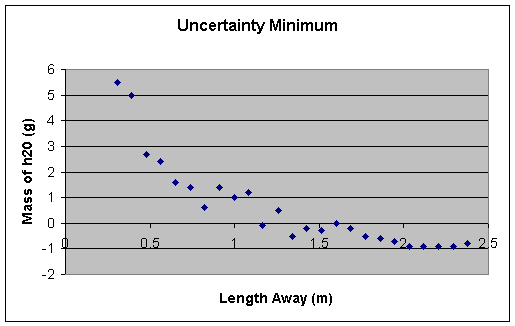
     There are some possible problems with the uncertainty however. First off, on the minimum uncertainty it is absurd for a tuna can to lose mass when water is added. That is why there are negative numbers for the tuna cans farthest away from the splash site. Also on the graph for the minimum uncertainty there is no trend line added because on all of the graphs the trend line is a power function. And it is not possible for the function (say y=x2) to come out negative. The thing about the uncertainty is that not all of the factors applied to each can. In some of the cans (mainly those closest to the splash site) there were rocks that I was unable to remove but there were none in others, so the graph of the mass of water proportional to the tuna cans length from the splash site would be more random. Like so:

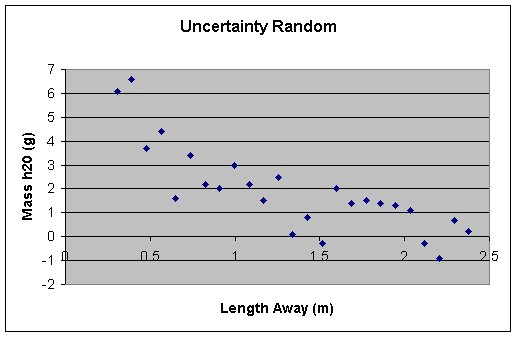
     That is always a possibility mathematically but is not logically. When viewing the tuna cans after the data collection, I easily could see that the cans closest to the splash site had much more water than those around the outside, so the data did match my hypothesis.