PreQuiz 12.3 .:. Go Up

Refraction/Interference

Solved by Lindsey Pozo and Alex Schrimp

 

1. In my classroom, you are 1.45 m from one of the stereo speakers, and 3.21 m from the other.  If the wavelength is .391 m, what kind of interference do you have, constructive or destructive?  (Is it loud or quiet?) How many wavelengths difference in distance is there?  (4.5 wavelengths – destructive or quiet)

 

|L1-L2| / λ

|3.21 - 1.45| / .391 = 4.501 wavelengths

This equals approximately 4.5 wavelengths

If the wavelengths ends in .5 (such as 1.5 λ, 2.5 λ, 3.5 λ...etc) the type of interference is destructive (quiet).

If the wavelength is a whole number (such as 1.0, 2.0, 3.0...etc) the type of interference is constructive (loud)

 

Questions 2-5 are about the light from a 640 nm laser.  (640 nm is its wavelength, 1 nm = 10^-9 m)

2. What is the speed of the laser light in Lucite? (n = 1.51) (1.99x10⁸ m/s)

 

 Formula is... n=c/v

c is a constant, c= speed of light = 3*10^8

n is given, n= 1.51

You are solving for v.

 

1.51 / 1 = (3*10^8) / v

Cross Multiply!

V= 198675496.7

V= 1.99*10^8 m/s

 

3. What is the wavelength and frequency of the light in Lucite? (n = 1.51) (424 nm, 4.69x10¹⁴ Hz)

 

 Formula for both wavelength and frequency is... V=f λ

 ***To find frequency: v= speed of light= 3*10^8

Use the wavelength that is given= 640 * 10^-9

Solving for f!

 

3E8=f (640E-9)

Divide 3*10^8 by 640*10^-9

F= 4.6875 *10^14 Hz

 

***To find the wavelength: Use the velocity from question 2

Use the frequency that you just found. You are now solving for the wavelength.

1.98*10^8= (4.6875*10^14) λ

Divide 1.98*10^8 by (4.6875*10^14) to find the wavelength

    λ=4.24*10^-7 m or 424 nm

 

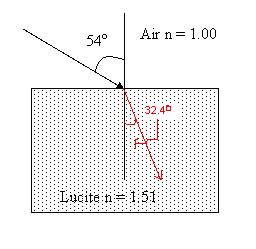
4. The laser goes from air into the Lucite. It makes the angle shown in the diagram below. Calculate the refracted angle in the Lucite, draw the refracted beam, and label the angle (32.4 degrees)

 

n₁/n₂= sin θ₂/ sin θ₁

 

n₁= 1

n₂= 1.51

The incident angle or sin θ₁ = 54

 

1/1.51= sin θ / sin 54

Cross multiply!

Sin 54=1.51sin θ

 

Divide each side by 1.51

Sin 54/ 1.51 =1.51sin θ / 1.51

Sin θ = .53577

Take the inverse sign of .53577

Θ= 32.396 or approximately 32.4 degrees

32.4 degrees is the refractive angle in the Lucite.

 

 

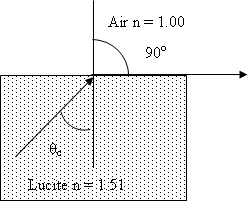
5.  What is the critical angle between air and Lucite?  In which substance does it occur? (41.5^o – in the Lucite)

 

 

 

 

N₁/N₂= sin θ₂/ sin θ₁

 

N1= 1.51

N2=1.00

θ₂ = 90

θ₁=???

 

1.51 /1.00 = sin 90 / sin θ

Now cross multiply and divide!

1.51(sin θ) = sin90(1)

Divide both sides by 1.51

1.51(sin θ) / 1.51 = sin90(1) / 1.51

Sin θ = .66225

Take the inverse of sin.

Inverse sin(.66225) = 41.47

θ = 41.47 degrees = approximately 41.5 degrees

 

****The angle in the faster medium (in this case, θ₂) is always 90 when solving for a critical angle.

 Critical angles are always the arcsin(n₂/n₁)