PreQuiz 12.1 - Standing Waves .:. Go Up

 

The Formula:
 

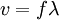
v = wave speed in m/s
f = frequency in Hz (1/s)
l = wavelength in m

The Prequiz:

Show your work, and circle your answers and use sig figs to receive full credit.

1-3. A guitar string has a length of 64.5 cm, and a fundamental frequency of 110. Hz. 

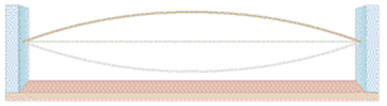
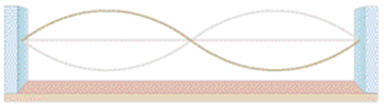
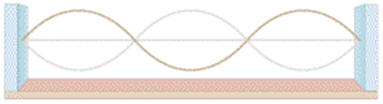
1. Draw the first three harmonics of vibration on the string below, and calculate the wavelength and frequency  for each.

 

 

 

 

 

 

 

 This is the fundamental - we know its frequency is 110. Hz, and that the string is 0.645 m long.

 

Set up a number sentence:
0.645 m = 2/4l, l = 1.29 m

 Set up a number sentence:
0.645 m = 4/4l, l = 0.645  m

For this type of standing wave, the second harmonic frequency is twice the fundamental, f = 220. Hz

 Set up a number sentence:
0.645 m = 6/4l, l = 0.430  m

For this type of standing wave, the third harmonic frequency is thrice the fundamental, f = 330. Hz

2. What is the velocity of the waves on this string? (142 m/s)

 

 Use v = fl for any of the frequencies or wavelengths above.  You should get the same answer three times because it is the same string.

 f = 110. Hz
l = 1.29 m
v = 141.9 = 142 m/s

 

3. If this string is fingered 21.5 from one end (it is shortened by that amount).  What is the frequency of the fundamental now? (165 Hz)

 

The new length of the string is 0.645 m - 0.215 m = 0.430 m
For the fundamental, set up a number sentence:
0.430 m = 2/4l, l = 0.860 m

Finally, use the equation v = fl to find the new frequency:
 

l = 0.860 m
v = 141.9 m/s

 f = 165 Hz

 

4. Calculate the wavelengths below.  The length given is the length of the waveform (The picture)

 

 

 L = 45 cm

 

 L = 2.67 m

 

 L = 68 cm

 Set up a number sentence:
45 cm = 5/4l, l = 36 cm

Set up a number sentence:
2.67 m = 4/4l, l = 2.67 m

 Set up a number sentence:
68 cm = 2/4l, l = 136 cm

5. Draw the second harmonic (The second lowest tone it can make.) of a one end fixed, one end open pipe.  Calculate the frequency of this mode if the pipe is 13.2 cm long, and the speed of sound in the pipe is 317 m/s. (1801 -> 1.80 x 103 Hz)

 

First, you need to be able to draw the harmonics of one end fixed, one end open.  (Read your book??)  The second harmonic looks like this:

Set up a number sentence:
13.2 cm = 3/4l, l = 17.6 cm = 0.176 m

 

Finally, use the equation v = fl to find the frequency:
 

l = 0.176 m
v = 317 m/s

 f = 1801.14 Hz = 1.80 x 103 Hz