PreQuiz 6.1 - Energy .:. Go Up
The Formulas:
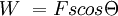
W = work in Joules
F = Force in Nq = angle twixt F and s
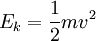
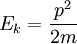
Ek = Kinetic energy of a moving object in J
m = mass in kg
v = speed in m/s
p = momentum in kgm/s
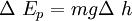
Ep = gravitational potential energy in J
m = mass in kg
g = 9.81 kgm/s/s on earth
Dh = change in height in m
The Prequiz:
1. A 5.2 kg object speeds up from 3.1 m/s to 4.2 m/s. What is the change in kinetic energy? (21 J)
This is a general question using the formulas for energy.
Kinetic (the energy of a moving object) is Ek = 1/2mv2 (m = mass, v = speed)
gravitational potential is Ep = mgh, (m = mass, g = gravitational acceleration, h = change in height)
and work is W = Fs cosq. (F = force, s = displacement, and q = angle twixt F and s)
finally, elastic potential (not in the data packet) is Ep = 1/2kx2. (k = spring stiffness in N/m, and x = spring stretch or compression distance)
In this case, the change in kinetic energy is the difference between that at the two different speeds:
Difference = 1/2(5.2 kg)(4.2 m/s)2, - 1/2(5.2 kg)(3.1 m/s)2, = 21 J
2. A 1.2 HP motor (1 HP = 745.7 Watts) is used to raise a 1300 kg Land Rover 5.7 m up into a tree. What time will it take? (81 s)
This question is about power. Power is really the rate at which work is done (1 Watt = 1 Joule/second)
so the general form is:
Power = (any change in energy)/(the time it took)
It can also be written as it is in your data packet:
Power = Fv.
In this case, the work to be done is the change in the Land Rover’s potential energy:
Work = mgh = (1300 kg)(9.81 m/s/s)(5.7 m) = 72,692.1 J.
The power of the winch in Watts is
(1.2 HP)(745.7 W/HP) = 894.84 W
and finally, the time:
Power = (any change in energy)/(the time it took)
894.84 W = (72,692.1 J)/(the time it took)
so time = 81 s
Problems 3, 4, 5:
These last three problems are conservation of energy problems. The basic idea here is:
Total energy before = Total energy after
So you read the problem, draw a picture, and figure out which energy equations you need to need to use on each side of the equation. Once you get the picture in your head, the only tricky part really is to figure out which side work goes on. The general rule is that if the force that does the work is speeding the object up, it is a “before” or left side work, and if it slows the object is goes on the right side.
Problem 3 is always 1 to 1 – one kind of energy on the left side, and one kind on the right, 4 is 2 to 1 or 1 to 2, and the last problem is 2 to 2.
3. A massless spring with a spring constant of 34 N/m is compressed 5.8 cm horizontally and used to shoot an 18 gram marble across a frictionless table. What is the speed of the marble? (2.5 m/s)
For this problem, the spring’s potential energy is being turned into the marble’s kinetic energy:
1/2kx2 = 1/2mv2
1/2 (34 N/m)(0.058 m)2 = 1/2 (0.018 kg)(v)2
so v = 2.5 m/s
4. A 3.4 kg bowling ball hanging from the ceiling on a long string swings from side to side like a pendulum. When it is 15 cm above its lowest point on the left side, I shove it with a force of 11 N for a distance of .35 m in the direction it is going. How high will it swing on the other side? (Neglect friction) (27 cm)
In this problem the bowling ball swings from left to right. The left side is “before”, and assuming the ball starts from rest, we have on the left side of the equation we have the potential energy of the ball and the work done in speeding it up, and on the right side (when it has swung to a stop at its highest point) it has only potential:
mgh + Fs = mgh
(3.4 kg)(9.81 m/s/s)(0.15 m) + (11 N)(0.35 m) = (3.4 kg)(9.81 m/s/s)h
so h = 0.27 m or 27 cm
5. A 580 kg rollercoaster is going 7.5 m/s on the top of a 1.2 m tall hill, how fast is it going on top of a 3.5 m tall hill? (Neglect friction) (3.3 m/s)
This is a classic roller coaster problem. The first hill is before, and the second after. Before and after it has both kinetic and gravitational potential:
mgh + 1/2mv2 = mgh + 1/2mv2
(580 kg)(9.81 m/s/s)(1.2 m) + 1/2(580 kg)(7.5 m/s)2 = (580 kg)(9.81 m/s/s)(3.5 m) + 1/2(580 kg)v2
so v = 3.3 m/s