Planes and Pulleys – Solutions .:. Go Up
– I have used the convention in applying Newton’s second law to make all forces, displacements, velocities and accelerations down the plane negative, and up the plane positive. The “parallel force” (F||) is just the component of gravity that is parallel to the plane. The Perpendicular force (Fperp) is the component of weight perpendicular to the plane.
-By Paul Herstedt and Chris Murray
1. A 2.15 kg block of wood is on a frictionless inclined plane that makes an angle of 35.0o with the horizontal. a) Find F||, and Fperp b) If the block is released on the plane, what will be its acceleration down the plane? c) What force in what direction would prevent it from accelerating down the plane?
a)
OK, basically,
F|| = (2.15)*9.8*sin(35) = 12.085N = 12.1 N
Fperp = (2.15)*9.8*cos(35) = 17.260N = 17.3 N but since there is no friction the Fperp is not terribly useful.
b)
Since there is no friction, and no other things like jet engines, strings, or little men pushing or pulling on the block, the only force along the plane is the F|| of 12.085N down the plane (-). So our expression of Newton’s second law becomes:
F = ma,
<-12.085 N> = (2.15 kg)a, (the parallel force is negative because down the plane is negative)
so a = -5.621 m/s/s = -5.62 m/s/s (down the plane).
c)
Since there is no friction to help the block stay on the plane, you would need to cancel out the 12.085N of weight parallel to the plane, and exert exactly that force up the plane. Having so done, you would prevent the block from accelerating up or down the plane, but it could still move at a constant velocity in any direction. +12.1 N up the plane
2. A 5.00 kg block of wood is on a frictionless 13 m long inclined plane that makes an angle of 47o with the horizontal. a) Find F||, and Fperp b) If the block is released on the plane, what will be its acceleration down the plane? c) What time will it take to slide down the plane if it is released at the top from rest? d) What force in what direction will make the block accelerate up the plane at 4.50 m/s/s? e) What force in what direction will make the block accelerate down the plane at 4.50 m/s/s?
a)
Again,
F|| = (5.00)*9.8*sin(47) = 35.836N = 36 N
Fperp = (5.00)*9.8*cos(47) = 33.418N = 33 N again, not terribly useful.
b)
Since there is no friction Newton’s second law is simple. The only force acting along the plane is the parallel component of gravity down (-) the plane. Making down the plane negative:
<-35.836 N> = (5.00 kg)a, so a = -7.167 m/s/s = -7.2 m/s/s (down the plane).
c)
s = -13, u = 0, a = -7.167 m/s/s, use s = ut + 1/2 at2. t = 1.905 s = 1.9 s
d)
So you have some unknown force up the plane (+), and the parallel component of gravity 35.836N down (-) the plane, and the acceleration is up (+) the plane, so your expression of Newton’s Second law becomes
<+F – 35.836> = (5.00 kg)(+4.50 m/s/s) making up the plane positive. F = 58.336N = +58 N
e)
Now we have the parallel force of 35.836 down the plane (-), and a force (F) that could be up or down the plane such that the box accelerates at 4.5 m/s/s down (-) the plane. (I know it needs a force up the plane, as the box, unfettered, will accelerate at 7.167 m/s/s down the plane) Newton’s second law gives us
<F – 35.836 N> = (5.00 kg)(-4.50 m/s/s) where the acceleration is negative because we are accelerating down the plane, and up the plane is positive. F = 13.336 N = +13 N. Since it is positive, it is up the plane.
3. A block of Spam is on a frictionless inclined plane that makes an angle of 35o with the horizontal. a) If the Spam is released on the plane, what will be its acceleration down the plane? If the Spam is given a velocity of 5.0 m/s up the plane, b) how far up the plane will the block slide before coming back down, and c) what time will it take for the block to come back down to where it was released?
a)
OK, we don’t know the mass of the Spam, but we do know that it is tasty, and also some kind of meat. Don’t let this bother you. (Not knowing the mass) The mass will cancel, or the problem is unsolvable, except in terms of m. Leave m in, and solve it that same way.
F|| = m*9.8*sin(35) = 5.621m
Fperp =m*9.8*cos(35) = 8.028m again, not terribly useful as the plane is frictionless.
Since there is no friction the parallel force is the only force acting along the plane (down -) , so Newton’s second law is very simple to express:
<-5.621m> = ma, and m cancels from all terms, giving a = -5.621m/s/s = -5.6 m/s/s (down the plane) Pretty easy, huh?
b)
Solving linear kinematics, the initial velocity is up the plane (+) and the acceleration is down (-)
s = ?, u = +5.00 m/s, a = -5.621 m/s/s, v = 0 (when it reaches the top). t = ?
Use v = u + at, t = .890 s,
s = (u+v)/2*t, s = 2.224 m = +2.2 m
c)
Since there is no friction, the acceleration is the same for the block as it moves up or down the plane, and so we can simply double the amount of time it took to go up the plane (it’s like throwing a ball up in the air) so the time to return is t = 2*.890 = 1.78 s = 1.8 s (When there is friction, the block decelerates on the way up much more quickly as it is opposed by the parallel component of gravity and friction, and accelerates more slowly down the plane. See problems 5-8)
4. A thing is on a frictionless 3.2 m long inclined plane that makes an angle of 47o with the horizontal. a) If the thing is released on the plane, what will be its acceleration down the plane? b) What time will it take to slide down the plane if it is released at the top from rest?
a)
OK, again, we don’t know the mass of the thing, so let’s leave m in, and solve it that same way.
F|| = m*9.8*sin(47) = 7.167m
Fperp =m*9.8*cos(35) = 6.684m again, not terribly useful as the plane is frictionless.
Since there is no friction, the only force is the parallel force down (-) the plane. Our expression of Newton’s law is simply:
<-7.167m> = ma, and m cancels from all terms, giving a = -7.167 m/s/s = -7.2 m/s/s (down the plane)
b)
s = -3.2, u = 0, a = -7.167 m/s/s, v = ?, t = ?
Use s = ut + 1/2at2, t = .9450 s = .94 s
5. The plane and pulley are frictionless for a) – d). e) has a bit o’ friction
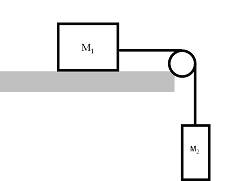
a) If M1 has a mass of 23.1 kg, and M2 has a mass of 5.63 kg, what is the tension in the string, and the acceleration of the system?
For problems with a string we need to set up two <F> = ma problems, and then solve they system of equations.
1. First, let’s choose the direction for positive acceleration – this one’s obvious – M1 will accelerate to the right, and M2 down. (This becomes the positive direction for each of them)
2. Next – we set up the <F> = ma (Newton’s second law) expression for each mass:
a. For M1: T = (23.1 kg)a (There is only the tension in the string T acting to the right (+))
b. For M2: (5.63 kg)(9.81 N/kg) – T = (5.63 kg)a (We have the weight acting down (+) and the tension T acting up (-))
3. And finally we solve the system. If the pulley is frictionless, it is out of the picture, so we can always solve these by simply adding the equations together to make T, (which is positive in one, and negative in the other) drop out:
T = (23.1 kg)a
(5.63 kg)(9.81 N/kg) – T = (5.63 kg)a
(5.63 kg)(9.81 N/kg) = (23.1 kg + 5.63 kg)a
so a = 1.92239 m/s/s = 1.92 m/s/s
and now we just solve for the tension T by using one of our formulas, and then checking it in the other:
T = (23.1 kg)a = (23.1 kg)(1.92239 m/s/s) = 44.407 = 44.4 N
and plugging this into the other formula to check:
(5.63 kg)(9.81 N/kg) – T = (5.63 kg)a
(5.63 kg)(9.81 N/kg) – 44.407 N = (5.63 kg)a
a = 1.92239 (which is good – that’s what we got – we have definitely found the a and T that makes the system of equations work.
b) If M1 has a mass of 2567 kg, and M2 has a mass of 1.00 kg, what is the tension in the string, and the acceleration of the system?
This is just like a), so let’s go to the formulas:
T = (2567 kg)a
(1.00 kg)(9.81 N/kg) – T = (1.00 kg)a
(1.00 kg)(9.81 N/kg) = (2567 kg + 1.00 kg)a
so a = .0038200935 m/s/s = 3.82 x 10-3 m/s/s
(if M1 >> M2 (M1 is much greater than M2) then a (acceleration) must approach zero)
and T = (2567 kg)a = (2567 kg)(.0038200935 m/s/s) = 9.8062 = 9.81 N
(if M1 >> M2 then T must approach the weight of the hanging mass)
c) If M1 has a mass of 1.00 kg, and M2 has a mass of 500. kg, what is the tension in the string, and the acceleration of the system?
This is just like a), so let’s go to the formulas:
T = (1.00 kg)a
(500. kg)(9.81 N/kg) – T = (500. kg)a
(500. kg)(9.81 N/kg) = (1.00 kg + 500. kg)a
so a = 9.79042 m/s/s = 9.79 m/s/s
(if M1 << M2 (M1 is much smaller than M2) then a (acceleration) must approach gravity)
and T = (1.00 kg)a = (1.00 kg)(9.79042 m/s/s) = 9.79042 = 9.79 N
(if M1 << M2 then T must approach the weight of the mass on the plane)
d) If M1 has a mass of 35.0 kg, what does M2 need to be so that the system has an acceleration of 3.15 m/s/s?
Ok – a bit different, we know M1, but have to calculate M2:
T = (35.0 kg)(3.15 m/s/s)
(M2)(9.81 N/kg) – T = (M2)(3.15 m/s/s)
(M2)(9.81 N/kg) = (35 kg + M2)(3.15 m/s/s)
So we do a bit of math:
9.81M2 = (35)(3.15) + 3.15M2
And
6.66M2 = 110.25
Finally
M2 = 16.554 = 16.6 kg
This makes sense, as if we try the solution for the acceleration, which is generally (weight of hanging mass)/(total mass) we get:
a = (16.554 kg)(9.81 kg)/(16.554 kg + 35.0 kg) = 3.15 m/s/s – so I bet we’re right.
e) Answer part a) but include a 17.2 N friction force on the block on the plane that resists the acceleration as it moves to the right.
Let’s solve this the way we solve such things:
- First, let’s choose the direction for positive acceleration – this one’s a bit less obvious than a) because of the friction force. M1 will accelerate to the right, and M2 down. (This becomes the positive direction for each of them. If we have guessed wrong, we will get a negative acceleration)
- Next – we set up the <F> = ma (Newton’s second law) expression for each mass:
- For M1: <T – 17.2 N> = (23.1 kg)a (There is the tension in the string T acting to the right (+), and because the block is sliding to the right, a force of 17.2 N to the left (-))
- For M2: <(5.63 kg)(9.81 N/kg) – T> = (5.63 kg)a (We have the weight acting down (+) and the tension T acting up (-))
- And finally we solve the system. If the pulley is frictionless, it is out of the picture, so we can always solve these by simply adding the equations together to make T, (which is positive in one, and negative in the other) drop out:
T - 17.2 N = (23.1 kg)a
(5.63 kg)(9.81 N/kg) – T = (5.63 kg)a
(5.63 kg)(9.81 N/kg) – 17.2 N = (23.1 kg + 5.63 kg)a
so a = 1.3237 m/s/s = 1.32 m/s/s
and now we just solve for the tension T by using one of our formulas, and then checking it in the other:
T – 17.2 = (23.1 kg)(1.3237 m/s/s), T = 47.778 = 47.8 N
and plugging this into the other formula to check:
(5.63 kg)(9.81 N/kg) – 47.778 = (5.63 kg)a
a = 1.3237 (which is good – that’s what we got – we have definitely found the a and T that makes the system of equations work.
6. The plane and pulley are frictionless.
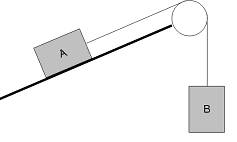
a) If A and B both have a mass of 5.0 kg, and the plane makes an angle of 25o with the horizontal, what is the acceleration and the tension in the cable?
The difference between this problem and problem #5 is that there is a slant in A’s direction. In order to solve for the gravitational pull on A on a 25o slant, we use 9.81(sin(25o)). With that in mind, we can set up our system of equations.
T – (5 kg)(9.81 N/kg)(sin(25o)) = (5 kg)a
(5 kg)(9.81 N/kg) – T = (5 kg)a
(5 kg)(9.81 N/kg) – (5 kg)(9.81 N/kg)(sin(25o)) = (5 + 5 kg)a
Once solved, we get a = 2.832 m/s/s = 2.8 m/s/s.
We can then plug in our acceleration into either of the tension equations to solve for T.
T – (5 kg)(9.81 N/kg)(sin(25o)) = (5 kg)(2.8 m/s/s)
Our cable’s tension comes out to be 34.73 N = 35 N
b) Solve as in problem a), but give A a mass of 5.0 kg, and B a mass of 1.78 kg.
Exact same procedure, but now we’ll use 1.78 kg in place of B’s mass.
T – (5 kg)(9.81 N/kg)(sin(25o)) = (5 kg)a
(1.78 kg)(9.81 N/kg) – T = (1.78 kg)a
(1.78 kg)(9.81 N/kg) – (5 kg)(9.81 N/kg)(sin(25o)) = (5 + 1.78 kg)a
a = 0.4823 m/s/s = 0.48 m/s/s
T – (5 kg)(9.81 N/kg)(sin(25o)) = (5 kg)(0.48 m/s/s)
T = 18.33 N = 18 N
c) Suppose A has a mass of 4.51 kg, and accelerates from rest 3.27 m up the ramp in 1.81 seconds. What must the mass of B be?
In order to solve this, we must first find the acceleration up the ramp that the 4.51 kg mass does. We can use SUVAT with the 3.27 m and the 1.81 s to find the acceleration.
s = ut + ½at2 Since it accelerates from rest, u is 0
a = 2s / t2
a = 2 (3.27 m) / (1.812)
a = 1.9962 m/s/s
With our newfound acceleration, we can set up one of our tension equations to solve for T. Since we solved for the acceleration in A, and we also have the mass, the only variable we have left to solve for is T.
T – mg = ma
T – (4.51 kg)(9.81 N/kg)sin(25) = (4.51 kg)(1.99 N/kg)
T = 27.701 N
We can now plug the tension into the equation for B, finding mass.
mg – T = ma
mg – ma = T
m(g – a) = T
(g – a) = T / m
(9.81 N/kg – 1.99 N/kg) = 27.701 N / m
m = 3.54 kg
d) If the plane angle is 30o and A is 15 kg, what should the mass of B be to prevent acceleration?
If our acceleration is 0, we can set up our equation for tension like this.
T – mg = ma
T – (15 kg)(9.81 N/kg)(sin(30)) = (15 kg)(0 N/kg)
T = 73.575 N
Plugging the tension into the equation for B,
mg – T = ma
m(9.81 N/kg) – 73.575 N = m(0 N/kg)
m = 7.5 kg
7. The plane and pulley are frictionless, and the plane makes an angle of 21.0o with horizontal.
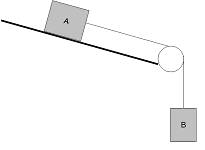
a) If A has a mass of 5.00 kg, and B 4.30 kg, what are the acceleration and the tension in the cable?
Similar to 6, this scenario is the same idea with forces in the same direction because of the slope instead of the opposite. Because the forces are act in the same direction, the two (mg)s will be added together.
T + (5 kg)(9.81 N/kg)(sin(21o)) = (5 kg)a
(4.3 kg)(9.81 N/kg) - T = (4.3 kg)a
(4.3 kg)(9.81 N/kg) + (5 kg)(9.81 N/kg)(sin(21o)) = (5 + 4.3 kg)a
a = 6.4259 m/s/s = 6.43 m/s/s
Substituting (a) into one of the equations to solve for T:
T + (5 kg)(9.81 N/kg)(sin(21o)) = (5 kg)(6.43)
T = 14.57205 N = 14.6 N
b) If A has a mass of 3.12 kg, and the tension in the cable is 2.56 N, what must the mass of B be?
We have enough given information to solve for the acceleration in the tension equation for A.
T + mg = ma
(2.56 N) + (3.12 N)(9.81 N/kg)(sin(21o)) = (3.12 N)a
a = 4.3361 N/kg
With the uniform acceleration, we can solve for the mass of B.
m(9.81 N/kg) – 2.56 N = m(4.33 N/kg)
m = 2.56 N / (9.81 N/kg – 4.33 N/kg)
m = .467674 kg = .468 kg
c) Using the masses from part a), suppose you observed an acceleration of only 3.50 m/s/s. What frictional force must exist between A and the plane? (assume the plane is not frictionless)
Friction is a force subtracted from the tension of A, decreasing its acceleration. To set up our system of equations for finding friction (F):
T + F + mg = (m)a
mg – T = (m)a
mg + mg + F = (m1 + m2)a
T + F + (5 kg)(9.81 N/kg)(sin(21o)) = (5 kg)(3.5 N/kg)
(4.3 kg)(9.81 N/kg) – T = (4.3 kg)(3.5 N/kg)
(4.3 kg)(9.81 N/kg) + (5 kg)(9.81 N/kg)(sin(25o)) + F = (5 + 4.3 kg)(3.5 N/kg)
F = 27.21 N = 27.2 N
8.
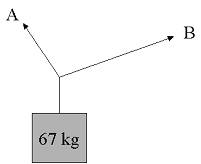
Cable A makes an angle of 63.0o with the horizontal, and B makes an angle of 23.0o with the horizontal. What is the tension in each cable for there to be no acceleration of the system?
The first thing to do is convert both angles into trig angles. B’s angle is already a trig angle, since the angle it makes is with the 0o horizontal. A, however, makes a 63o angle with the 180o horizontal. In order to convert this into a trig angle, we take 180o – 63o = 117o. With our correct angles, we can set up a system of equations that we can solve with a matrix.
A cos(117) + B cos(23) = 0
A sin(117) + B sin(23) = (67 kg)(9.81N/kg)
The question asks for no acceleration. In order to achieve that, the tension must balance vertically and horizontally. In the x direction, A and B must balance each other out to 0, considering the weight is only affecting the problem vertically. A and B must also balance out the weight (m*g) of the block. Therefore, the force that A and B pull up must be equal to the force the block pulls down. The matrix we will use will look like this:
[cos(177) cos(23)][A] = [ 0 ]
[sin(177) sin(23)][B] = [657.27]
Solving this will give you 606.4976 for A and 299.1229 for B.
A = 606 N
B = 299 N
9.
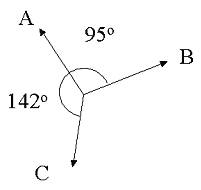
Cable A has a force of 23 N along it, what must be the tensions in cable C and B for there to be no acceleration of the system?
As we did in the last problem, we will need to convert all angles to trig angles. However, there is no horizontal this time. Also, there is no gravity acting on anything, all forces are tensions in cables. With no gravity, there is no distinct place, and we can choose any cable to be our horizontal. For the sake of this problem being easy, we can use cable A as our horizontal, since we already have A’s force. Rotating to the system to make A be along 0o, B is 95 below 0o, making B = 360o – 95o = 265o. C is 142o, so its angle is 0o + 142o = 142o. With our newfound trig angles, we can set up a system of equations. We need each equation, again, to balance itself out to 0.
23 cos(0) + B cos(265) + C cos(142) = 0
23 sin (0) + B sin (265) + C sin (142) = 0
Simplifying our equations so they can be entered into a matrix:
23 (1) + B cos(265) + C cos(142) = 0
23 (0) + B sin (265) + C sin (142) = 0
B cos(265) + C cos(142) = -23
B sin (265) + C sin (142) = 0
Our matrix will be:
[cos(265) cos(142)] [B] = [-23]
[sin(265) sin(142)] [C] = [ 0 ]
Solving this in a calculator will give you B = 16.8841 and C = 27.3200
B = 17 N
C = 27 N
10.
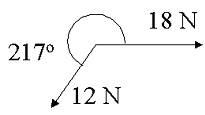
Find the third force (the equilibrant) that would prevent the system from accelerating.
|
Mag |
Trig angle |
x |
y |
|
18 N |
0o |
18 |
0 |
|
12 N |
217o |
-9.58 |
-7.22 |
|
Equilibrant |
|
-8.42 |
7.22 |
|
Sum |
|
0 |
0 |
With the x and y components, we can find the equilibrant’s angle magnitude. Tan-1(7.22/-8.42) = -40.61. However, since the x is negative and the y is positive, we know the angle has to be in quadrant II. Adding 180o to our answer will give us such an angle. 180 + -40.61 = 139.39o. *Note: If this concept is confusing, there is a drawing on problem 11 to help explain the same concept*. We can now find the magnitude using the Pythagorean Theorem.
8.422 + 7.222 = X2
X = 11.09165 N = 11 N
So, our angle magnitude for the missing angle is 11 N @ 139o.
11.
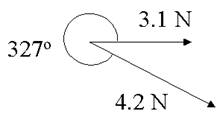
Find the third force (the equilibrant) that would prevent the system from accelerating.
|
Mag |
Trig angle |
x |
y |
|
3.1 N |
0o |
3.1 |
0 |
|
4.2 N |
327o |
3.522 |
-2.287 |
|
Equilibrant |
|
-6.622 |
2.287 |
|
Sum |
|
0 |
0 |
We can do the exact same thing as the last problem, finding our angle magnitude for the missing equilibrium. Tan-1(2.287/-6.622) = -19.053. Since the x is negative and the y is positive, the angle will be in quadrant II. In order to achieve that, we add 180o to the answer to get our trig angle. Here is a drawing that may better explain this:
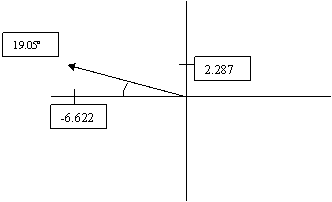
180 + -19.05 = 160.95o
To find the magnitude, Pythagorean Theorem:
6.6222 + 2.2872 = X2
X = 7.0058 N = 7.0 N
The answer comes to be 7.0 N @ 161o.