Problem Set T4.3: CHAPTER 12: | 39 | 51 | 52 | 53 | 54 | 55 | 57 | 60 | 63 | 73 | 77 | 78 | 86 |
CHAPTER 23: | 26 | 27 | 30 | 31 | 32 | 33 | 40 | 41
| CHAPTER 24: | 2 | 3 | 4 | 5 | Go up
- by To Chong, Sonja Scherer, Chris Murray, and Kendall
Houghton 2002. Revised 2009.
CHAPTER 12
39. How many overtones are present within the audible range for a 2.44-m-long organ pipe at 20 °C (a) if it is open, and (b) if it is closed ?
(a) If the organ pipe is open, the wavelength must be: l = 2L = 2.44 x 2 = 4.88 m
The fundamental frequency is: f = v/l =
343/4.88 = 70.3 Hz
The highest audible range is: fn = nf1 =
20,000 Hz
Therefore, we have: 70.3n = 20,000 <=> n = 284.5 = 284
But it's not all since the fundamental frequency is in the audible range.
Therefore, the total overtone is: 284 - 1 = 283
(b) If the organ pipe is closed, the wavelength must be: l = 4L = 2.44 x 4 = 9.76 m
The fundamental frequency is: f = v/l =
343/9.76 = 35.1 Hz
The highest audible range is: fn = nf1 =
20,000 Hz
Therefore, we have: 35.1n = 20,000 <=> n = 569
However, in the closed pipe, only odd harmonics are present. Otherwise, the
fundamental frequency is in the audible range; thus, the total overtones
is:
(569 - 1)/2 = 284
51. If the predominant frequency of a certain police car's siren is 1800 Hz when at rest. What frequency do you detect if you move with a speed of 30.0 m/s (a) toward the car, and (b) away from the car ?
For this problem, we have to use Doppler effect.
The source is at rest, the observer is moving.
(a) When you move toward the car, we have to use the formula:
f' =f[(v+uo)/(v)]
Since we are the ones moving, we use the moving source formula in the data booklet. We know it is plus, because we want a higher frequency, as the two are getting closer together.
This solves:
f’=1800[(343+30)/(343)]
f’=1957.4 Hz
(b) When you move away from the car, we have to use the formula:
f'= f[(v-Uo)/(v)]
The formula is still the moving observer one, however we change the addition sign to subtraction because we know we want a lower frequency, as the two are getting farther apart.
f’=1800[(343-30)/(343)]
f’=1642.56 Hz
52. A bat at rest sends out ultrasonic sound wave at 50,000 Hz and received them return from an object moving radially away from it at 25.0m/s. What is the received sound frequency?
For this problem, there are two basic steps to go:
At first, the bat is the source
at rest, and the object is moving away from the bat. Thus we utilize the
moving observer formula for the sound. Additionally, the formula uses
subtraction as the sound is moving away.
f' = f [(v+uo)/(v)]
f’=50,000[(343-25)/(343)]
f’ = 46355.7Hz
Secondly, we again have to use the Doppler effect. The bat now is a stationary observer, but the object is moving source. Thus we utilize the moving source formula using addition.
f’=f[(v)/(v-uo)]
f’=46355.7[(343)/(343+25)
f’=43206.5 Hz
(Table of contents)
53. In one of the original Doppler experiments, one tuba was placed on a moving platform car at a frequency of 75Hz, and a second identical one was played on the same tone while at rest in the railroad station. What beat frequency was heard if the train approached the station at a speed of 10.0m/s?
Assuming we are on the train station listening to both the Tuba on the station and the one on the train. The Tuba that is approaching us is a moving source, shifted higher:
f' = f [v/(v + us)]
f’=75[343/(343-10)]
f’=77.3 Hz
The beat frequency is the difference between those two above frequencies: fbeat
= 77.3 - 75
fbeat = 2.3 Hz
54. Two automobiles are equipped with the same single frequency horn. When one is at rest and the other is moving toward an observer at 15m/s, a beat frequency of 5.5 Hz is heard. What is the frequency the horns emit? Assume T = 200C.
In this problem, the observer is
at rest and the source is moving toward the observer, so the beat frequency is
between the original frequency f and the Doppler shifted frequency using the
moving source formula.
fbeat = f' - f
and if we solve for the Doppler shifted frequency, we get
f' = f + fbeat
From the Doppler effect, we have:
f’=f[(v)/(v-uo)]
Therefore:
f + fbeat =
f[(v)/(v-uo)]
And finally, you just need to solve for the original frequency f:
f + fbeat = f[(v)/(v-uo)]
fbeat = f[(v)/(v-uo)] - f
5.5 = f[(343)/(343-15)]-f
5.5=(f)(1.046)-(f)
5.5=1.046f-1f
5.5=.046f
120 Hz = f
55. Two trains emit whistles of the same frequency of 277 Hz. If one train is at rest and the other is traveling at 40km/h away from an observer at rest, what beat frequency will the observer detect?
40 km/hr/3.6 = 11.11 m/s
This is a moving source problem, so we know to use that formula. Also, We know
to use the + because we want a lower frequency as the train is going away from
us.
f’=f[(v)/(v+us)]
f' = 277[(343)/(343+40)
f' = 268.3 Hz
Then, we solve for the beat
frequency, which is:
fbeat = |f1 - f2|
fbeat = |277 Hz - 268.3 Hz|
fbeat = 8.7 Hz
(Table of contents)
57. Ultrasound waves are used to measure blood flow speeds. Suppose a device emits sound at 500 kHz, and the speed of sound in human tissue is taken to be 1540 m/s. What is the expected beat frequency if blood is flowing naturally in large leg arteries at 2.0 cm/s directly away from the sound source?
2 cm/s = .02 m/s
This is another reflection problem. There are two steps to solving it,
first, the object (blood in this case) is a moving "observer" and the
frequency it is reflecting is Doppler shifted, and then it becomes a moving
source. In both cases the shift is toward lower frequencies.
So the frequency of the
reflected sound is found using the moving observer formula:
f' = f [(v+uo)/(v)]
f’=500,000[(1540-.02)/(1540)]
f' = 499993.51 Hz
Then there is also a moving source shift from the object. We choose the + again, to make the frequency lower, as the object is going away from us:
f’=f[(v)/(v+uo)]
f’=499993.51[(1540)/(1540+.02)
f’=499987 Hz
Finally, the beat frequency is:
fbeat = |f1 - f2| = |500,000
Hz - 499987 Hz| = 13 Hz
(Table
of contents)
60. You are flying above the Gulf of Mexico in a police helicopter when you see fast moving boat below. The wake from the boat forms an angle of 200 on either side of the straight line motion. Knowing that the speed of the water waves is about 2.0m/s, what is the speed of the boat?
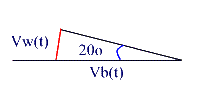
At some time t after a wave is emitted, the wave has traveled a distance
Vw(t) (where Vw is the wave speed, and t is the time) from the original
position of the boat, and the boat has traveled Vb(t) (Vb is the boat
velocity)along its path. Since the wave travels out spherically, the wake
touches a tangent of all the expanding spheres, and therefore is perpendicular
to the red line in the above diagram, which means we have a right triangle, and
its hypotenuse is Vb(t), and the side opposite the 20o angle is
Vw(t), using SOHCAHTOA,
sin(20o) = (Vw(t))/(Vb(t)) = (Vw)/Vb), and so Vb = Vw/sin(20o)
= (2.0 m/s)/sin(20o) = 5.8 m/s
(Table
of contents)
63. An airplane travels at Mach 2.3 where the speed of sound is 310m/s. (a) What is the angle the shock wake makes with the direction of the airplane's motion? If the plane is flying at the height of 7100 m, how long after it is directly overhead will a person on the ground hear the shockwave?
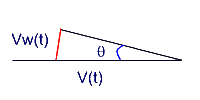
Mach 2.3 = 2.3(310 m/s) = 713 m/s
At some time t after a wave is emitted, the wave has traveled a distance Vw(t)
(where Vw is the wave speed, and t is the time) from the original position of
the plane, and the plane has traveled V(t) (V is the plane's velocity) along
its path. Since the wave travels out spherically, the wake touches a
tangent of all the expanding spheres, and therefore is perpendicular to the red
line in the above diagram, which means we have a right triangle, and its
hypotenuse is V(t), and the side opposite the angle is Vw(t), using
SOHCAHTOA,
sin(20o) = (Vw(t))/(V(t)) = (Vw)/V), so the angle = sin-1((310
m/s)/(713 m/s)) = 25.77o = 26o
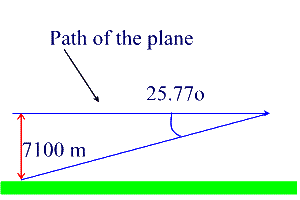
Now, since the airplane is 7100 m above the ground, it has traveled some
distance before the wake or shock wave hits us. Looking at the triangle
above, 7100 m is the opposite side of the 25.77o angle, and the distance
the plane has traveled is the adjacent side. So again using
SOHCAHTOA,
tan(25.77o) = OPP/ADJ = (7100 m)/straveled
where straveled is the distance the plane has traveled
so straveled = (7100 m)/tan(25.77o) = 14705.7 m
and it would take (v = s/t) t = s/v = (14705.7 m)/(713 m/s) = 20.6 s = 21 s
(Table of contents)
73. The A string of a violin is 32 cm long between fixed points with a fundamental frequency of 440 Hz and a linear density of 5.5x10-4kg/m. (a) What are the wave speed and tension in the string? (b) What is the length of the tube of a simple wind instrument (say, an organ pipe) closed at one end whose fundamental is also 440 Hz if the speed of sound is 343 m/s in air? (c) What is the frequency of the first overtone of each instrument?
Well, we can find the velocity by analyzing the standing wave.
At the fundamental, the string has two nodes at the end, and one anti-node in
the middle, so therefore the vibrating length of the string (.32 m) is equal to
2/4l, so l = .64 m
Now we can get the velocity by using v = ¦l
v = ¦l = (440 Hz)(.64 m) = 281.6 m/s, and now we can find the
tension.
Now we will apply a very very special formula from the data packet, which is: v =
/TÖµ
Where µ = mass/length for the cord, and T is the tension in the cord.
We have: T = ??; µ = 5.5x 10-4kg/m and v = 281.6 m/s
So find the tension T:
v = /TÖµ
v2 = /Tµ
T = v2µ =
(281.6 m/s)2(5.5x10-4 kg/m) = 43.6 N
The next two harmonics are simply multiples of this fundamental:
f1 = 440 Hz (fundamental frequency)
f2 = 2f1 = 2 x 440 Hz = 880 Hz
Now, if you want a standing sound wave of this frequency, its wavelength must
be
v = ¦l
l = v/f = (343 m/s)/(440 Hz) = 0.780 m
At the fundamental, a closed end pipe has an anti node at the open end, and a
node at the closed end, so that only a quarter of a wavelength fits inside the
pipe. So therefore:
L = 1/4l = 1/4(.780 m) = .195 m
and the next overtone would be three times the fundamental frequency, as closed
end pipes go in multiples of 1, 3, 5, 7... so f2 = 3(440) = 1320 Hz
(Table
of contents)
77. Two loudspeakers are at opposite ends of a railroad car as it moves past a stationary observer at 10.0 m/s, as shown in Fig. 12-37. If they have identical sound frequencies of 200 Hz, what is the beat frequency heard by the observer when (a) he observes from the position in A, in front of the car, (b) he is between the speakers as in B, and (c) he observes the speakers after they have passed him, as in C?
(a) When the stationary observer is at point A, the two sounds emitted from
the speakers have the same Doppler effect. Therefore, the beat frequency must
be 0.
(b) When the observer is at B, one source from one speaker is moving away from
him, the other is moving toward him. According to the Doppler effect, we have:
- Moving toward.
f' = f/(1 - vs/v) = 200/(1 - 10/343) = 206Hz
- Moving away
f' = f(1 + vs/v) = 200/(1 + 10/343) = 194Hz
Therefore, the beat frequency is: fbeat = 206 - 194 = 12 Hz
(c) When the stationary observer is at point C, the two sounds emitted from the
speakers have the same Doppler effect. Therefore, the beat frequency must be 0.
(Table of contents)
78. The frequency of a steam train whistle as it approaches you is 522 Hz. After it passes you, its frequency is measured as 486 Hz. How fast was the train moving (assume constant velocity)?
For this problem, we need two Doppler formulas:
You are the stationary observer, and the source is moving:
(a) Toward:
f' = f/(1 - vs/v) = vf/(v - vs)
(1)
(b) Away
f'' = f/(1 + vs/v) = vf/(v + vs)
(2)
The last step is not so fancy, but very important:
Divide (1) by (2), we have:
f'/f'' = (v + vs)/(v - vs)
Therefore, vs = v (f' - f'')/(f' + f'') = 343 x (522 - 486)/(522 +
486) = 12.25m/s
(Table of contents)
86. A bat flies toward a moth at speed 8.0 m/s while the moth is flying toward the bat at speed 5.0 m/s. The bat emits a sound wave of 51.35 kHz. What is the frequency of the wave detected by the bat after it reflects off the moth?
This is the mother of all doppler problems. First, the sound is source
shifted by the bat's 8.0 m/s, then observer and source shifted as it reflects
from the moth's 5.0 m/s, and finally the bat is a moving observer to the
reflected waves.:
1. Moving source from bat:
f' = f/(1 - vs/v) = (51.35 kHz)/(1-(8.0 m/s)/(343 m/s) = 52.57627
kHz
2. Moving observer from moth:
f' = f ( 1 + v0/v) = (52.57627 kHz)(1+(5.0 m/s)/(343 m/s)) = 53.3427
kHz
3. Moving source from moth:
f' = f/(1 - vs/v) = (53.3427 kHz)/(1-(5.0 m/s)/(343 m/s)) = 54.13178
kHz
And Finally,
4. Moving observer from bat:
f' = f ( 1 + v0/v) = (54.13178 kHz)(1+(8.0 m/s)/(343 m/s)) = 55.3943
kHz = 55.39 KHz
(Table
of contents)
CHAPTER 23
26. What is the speed of light in (a) crown glass, and (b) Lucite?
For this problem, we will use the formula: n = c/v
c = 3 x 108 m/s
(a) In crown glass, the index of refraction is: n = 1.52
v = c/n = 3 x 108/1.52 = 1.97 x 108 m/s
(b) In Lucite, the index of refraction is: n = 1.51
v = c/n = 3 x 108/1.51 = 1.987 x 108 m/s
(Table of contents)
27. The speed of light in ice is 2.29 x 108 m/s. What is the index of refraction of ice?
The index of refraction of ice is:
n = c/v = (3 x 108)/(2.29 x 108) = 1.31
(Table
of contents)
30. A flashlight beam strikes the surface of a pane of glass (n = 1.50) at a 630 angle to the normal. What is the angle of refraction?
The formula to find the angle of refraction is: n1sina1
= n2sina2
n1 = 1
Therefore, we have: sina2 = n1sina1/n2
= 1 x sin630/1.5 = 0.594
=> a2 = 36.440
(Table
of contents)
31. A diver shines a flashlight upward from beneath the water at a 42.50 angle to the vertical. At what angle does the light leave the water?
We have: n1sina1 = n2sina2
The index of refraction in water is: n1 = 1.33
The index of refraction in air is: n2 = 1
Therefore, the angle that the light leaves the water is:
a2 = sin-1(n1sina1/n2) =
sin-1(1.33 x sin42.50/1) = 640
(Table of contents)
32. A light beam coming from an underwater spotlight exits the water at an angle of 600. At what angle of incidence did it hit the air - water interface from below the surface?
We have: n1sina1 = n2sina2
The index of refraction in water is: n1 = 1.33
The index of refraction in air is: n2 = 1
Therefore, the angle of incidence that the light hits the air-water is:
a1 = sin-1(n2sina2/n1) =
sin-1(1 x sin600/1.33) = 410
(Table of
contents)
33. Rays of Sun are seen to make a 21.00 angle to the vertical beneath the water. At what angle above the horizon is the Sun?
n1sina1 = n2sina2
The index of refraction in water is: n2 = 1.33
The index of refraction in air is: n1 = 1
Therefore, the angle that the light leaves the water is:
a1 = sin-1(n2sina2/n1) =
sin-1(1.33 x sin210/1) = 28.50
The angle above the horizon is: 900 - 28.50 = 61.50
(Table
of contents)
40. What is the critical angle for the interface between water and Lucite? To be internally reflected, the light must start in which material?
In table 23-1 on page 696, you can find the indices of refraction of Lucite and water. Lucite is 1.51, and water is 1.33. The critical angle would refer to the light going from the slower to the faster medium, which in this case would be from Lucite to water. To solve a critical angle problem, use Snell's law, and set the refracted angle to 90o:
n1sina1 = n2sina2
(1.51)sin(a1) = (1.33)sin(90o) = 1.33
a1 is of course the critical angle.
a1 = sin-1(1.33/1.51) = 61.7o
It's pretty hard to get the direction wrong for the critical angle (i.e. from
which medium to which) as the sin-1(1.51/1.33)
is undefined, and therefore does not exist. (There is no critical angle
for travel that way)
(Table
of contents)
41. The critical angle for a certain liquid-air surface is 44.70. What is the index of refraction of the liquid?
To solve a critical angle problem, use Snell's law, and set the refracted angle to 90o:
n1sina1 = n2sina2
n1sin(44.7o) = (1.0003)sin(90o) = 1.0003
n1 = 1.0003/sin(44.7o) = 1.42
(Table of contents)
CHAPTER 24
2. Monochromatic light falling on two slits 0.042 mm apart produces the fifth order fringe at a 7.8o angle. What is the wavelength of the light used?
The fringes are the constructive interference which occurs at
nl = dsinq
Where n is the order, in this case, 5, so we have:
5l = dsinq
l
= dsin5/q
l
= (.042E-3 m)(sin(7.8o)/5) = 1.1x10-6 m = 1.1 mm
(Table
of contents)
3. The third-order fringe of 650 nm light is observed at an angle of 15o when the light falls on two narrow slits. How far apart are the slits?
The fringes are the constructive interference which occurs at
nl = dsinq
Where n is the order, in this case, 3, so we have:
3l = dsinq
d = 3l/sinq
d = (3(650x10-9 m))/sin(15o) = 7.5x10-6 m =
7.5 mm
(Table
of contents)
4. Monochromatic light falls on two very narrow slits .040 mm apart. Successive fringes on a screen 5.00 m away are 5.5 cm apart neat the center of the pattern. What is the wavelength and frequency of the light?
Simple way:
Small/Big = Small/Big
l/d = (Distance between
fringes)/(Distance to screen)
l/(.040x10-3 m) = (.055
m)/(5.00 m)
l = 4.4x10-7 m = 440 nm, and
the frequency is:
v = ¦l
, f = v/l
f = (3.00x108 m/s)/(4.4x10-7 m) = 6.8x1014
Hz
Exact way:
1l = dsinq
q = tan-1(.055 m/5.00m)
= 0.630o
1l = dsinq
= (.040x10-3m)sin(0.630o) = 4.39973x10-7m = 440 nm
(Table
of contents)
5. A parallel beam of light from a He-Ne laser, with a wavelength of 656 nm, falls on two very narrow slits .050 mm apart. How far apart are the fringes in the center of the pattern if the screen is 2.6 m away?
Let's do the simple way
Small/Big = Small/Big
l/d = (Distance between
fringes)/(Distance to screen)
(Distance between fringes) = (Distance to screen)l/d
= (2.6 m)(656x10-9 m)/(.050 x10-3) = 0.034112 m = 3.4 cm
Exact method
1l = dsinq
q = sin-1(l/d) = sin-1(656x10-9
m/.050x10-3 m) = 0.7517o
Distance between fringes = (2.6 m)tan(0.7517o) = 0.034114936 m = 3.4
cm
The two methods are very close for small angles
(Table
of contents)
What are you looking for?
You will never find him!!!
Gone, but not forgotten.