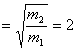Problem Set T4.1: 11:
| 1
| 2 |
3 | 4 | 6 | 8 | 9 | 13
| 14 | 17 | 18 | 19
| 21 | 26 | 28 | 29
| Schaum's 14: | 1 | 2 | 3
| 4
| 7 | 8 | 9 | Go up
- by To Chong, and Chris Murray, 2002
1. When a 65 kg person climbs into a 1000-kg car, the
car's springs compress vertically by 2.8cm. What will be the frequency of
vibration when the car hits a bump? Ignore damping.
I know that I can find the period using
T = 2p Öm/k
and since the frequency is the reciprocal of the period,
¦
= 1/T
Then once we find m and k we are set.
m is easy, once the person gets into the car the mass is 1000 kg + 65 kg or
1065 kg
k is a little harder. We know that the addition of the weight of a 65 kg
person compresses the springs 2.8 cm or .028 m. A 65 kg person weighs F
= ma, F = (65 kg)(9.8 N/kg) = 637 N
The compression distance, force and spring constant k are related
F = -kx
so
637 N = -k(-.028 m) (the car's springs push up, the compression is down)
k = 22750 N/m
m = 1065 kg
T = 2p Öm/k
= 1.36 s
¦
= 1/T = 0.74 Hz
(Table of contents)
2. An elastic cord is 65 cm long when a weight of 55 N
hangs from it and is 85 cm long when a weight of 80 N hangs from it. What is the
"spring" constant of this elastic cord?
When the stretching force increases by 25 N, from 55 N to 80
N, the length increases from .65 m to .85 m, an increase of .20 m. Use
the formula F = -kx on the amount of increase:
F = -kx
25 N = -k(-.20 m)
k = 125 N/m
(Table of contents)
3. If a particle undergoes SHM with amplitude 0.25m, what
is the total distance it travels in one period?
If it has an amplitude of .25 meters, that is the distance
above and below equilibrium it travels. If it starts above equilibrium,
it has completed one period when it returns to its original position, having
traveled .25 m down to equilibrium, .25 m below, .25 back, and .25 up to its
original position, for a total of 4(.25 m) = 1.00 m
(Table of contents)
4. A fisherman's scale stretches 3.9 cm when a 2.7-kg
fish hangs from it. (a) What is the spring constant and (b) what will be the
amplitude and the frequency of the vibration if the fish is pulled down 2.5 cm
more and released so that it vibrates up and down?
First off, the dude is weird to be pulling down on the fish
and making it vibrate up and down. Must be a Physics teacher. This
problem is just like problem 1:
I know that I can find the period using
T = 2p Öm/k
and since the frequency is the reciprocal of the period,
¦
= 1/T
Then once we find m and k we are set.
m is easy, its the mass of the fish which is 2.7 kg
k is a little harder. We know that the addition of the weight of a 2.7
kg fish stretches the springs 3.9 cm or .039 m. A 2.7 kg fish weighs F =
ma, F = (2.7 kg)(9.8 N/kg) = 26.46 N
The compression distance, force and spring constant k are related
F = -kx
so
26.46 N = -k(-.039 m) (the spring pulls up, the stretch is down)
k = 678.5 N/m = 680 N/m
m = 2.7 kg
T = 2p Öm/k
= 0.3964 s
¦
= 1/T = 2.5 Hz
And the amplitude of its motion would initially be the 2.5 cm more that the
fisherman pulled the fish. Note that fish tugging is prohibited in parts
of Indiana, and the seven western states, and is widely regarded as poor
sportsmanship.
(Table of contents)
6. A small fly mass 0.15g is caught in a spider's web.
The web vibrates predominately with a frequency of 4.0Hz. (a) What is the value
of the effective spring constant k for the web? (b) At what frequency would you
expect the web to vibrate if an insect of mass 0.50 g were trapped?
m = .15 g = .15 x 10-3 kg
I know I can bust this one apart with the relationship between period, mass
and spring constant:
T = 2p Öm/k
They give us the frequency of 4.0 Hz, which means it has a period of f =
1/T, so T = 1/f = .25 s
m = .15 x 10-3 kg, and plugging into
T = 2p Öm/k
k = 0.09475 N/m = 0.095 N/m
If a mass of .50 g or .5 x 10-3 kg were trapped in the web, we can
turn this spring constant around, and plug into
T = 2p Öm/k
m = .5 x 10-3 kg, k = 0.09475 N/m so
T = 0.4564 s
And finally, f = 1/T = 2.2 Hz
Now, just for fun, what if an old lady swallowed the same fly. Well,
assuming the fly undergoes SHM in her stomach, and her stomach can be treated
as a uniform cylinder..........
(Table of contents)
8. <Question goes here>?
Again, we will call on our friend
T = 2p Öm/k
for the .60 kg mass, f = 3.0 Hz, so since f = 1/T, T = 1/f = .3333 s
Plug into:
T = 2p Öm/k
k = 213.1836 N/m
Then plug in again using that spring constant, and the new mass of .38 kg:
T = 2p Öm/k
T = 0.2653 s
f = 1/T = 3.8 Hz
(Table of contents)
9. <Question goes here>?
Again, we will call on our friend
T = 2p Öm/k
for the .50 kg mass, f = 3.0 Hz, so since f = 1/T, T = 1/f = .3333 s
Plug into:
T = 2p Öm/k
k = 177.66 N/m
Let's solve c first for the total energy.
When the mass is the farthest from equilibrium (s = .15 m), its total energy
is stored in the spring in the form of potential energy:
Eelas = 1/2ks2
Eelas = total = 1.9986 J = 2.0 J
Now we are ready to pick off the other parts of the problem:
a) the maximum v:
At equilibrium, is has no potential energy, so therefore has all of its total
energy (1.9986 J), so solving for velocity:
Ek = 1/2mv2
Ek = 1.9986 J, m = .50 kg so
v = 2.8 m/s.
b) at position .10 m from equilibrium, it has some potential, and some
kinetic, but still a total energy of 1.9986 J, so our energy equation looks
like:
1.9986 J = 1/2mv2
+ 1/2ks2
s = .10 m, m = .50 kg, k = 177.66 N/m
so v = 2.1 m/s
d) And finally, the equation of motion if at t = 0 the displacement was a
maximum. This is going to be a sinusoidal function, although in this
case, since it starts at a maximum, we either need to shift the angle (can't
remember how), or use a function that is a maximum at t = 0. Hmm that
would be cosine.
so
x = xocoswt
xo = amplitude in this case .15 m, but what about w?
One clue to w
is the formula
a = -k/mx = -w2x,
this implies that w
= Ök/m
= 18.8 rad/s
Another clue is
y = Asin(wt ±
kx) where k = 2p/l and w
= 2p¦
(Which appears in the topic 4 formulas, it is the equation for a
traveling wave)
f = 3.0 Hz, so w = 2p¦
= 18.8 rad/s
Finally, putting it all into
x = xocoswt
x = (.15 m)cos(18.8t) = (.15 m)cos(2p(3.0
Hz))
(Table of contents)
13. <Question goes here>?
Assuming the elastic potential energy (Eelas
= 1/2ks2) all turns into
kinetic energy (Ek = 1/2mv2),
Set them equal
1/2ks2 = 1/2mv2
But we don't know k, but we soon will:
F = -kx, F = 80.0 N, and x = .200 m, so k = 400 N/m
So back to the energy equation
1/2ks2 = 1/2mv2
ks2 = mv2
v2 = ks2/m
v = sÖk/m,
k = 400 N/m, m = .150 kg, s = .200 m
v = 10.3 m/s
(Table of contents)
14. <Question goes here>?
m = 750 g = .750 kg
a) The first thing to do is find the period and frequency:
m = 750 g = .750 kg, k = 124 N/m
T = 2p Öm/k
T = 0.48865 s = .489 s
f = 1/T = 2.0464 Hz = 2.05 Hz
At amplitude, the
kinetic energy (Ek = 1/2mv2)
all turns into elastic potential energy (Eelas
= 1/2ks2),
Set them equal, and solve for s:
1/2mv2 = 1/2ks2
mv2 = ks2
s2 =
mv2/k
s = vÖm/k
v = 2.76 m/s, k = 124 N/m, m = .750 kg
s = 0.21465 m = 0.215 m
c) For the maximum acceleration use
a = -k/mx (the x you use would be the maximum x
of 0.21465 m)
k = 124 N/m, m = .750 kg, x = 0.21465 m
a = 35.5 m/s/s
d) The position as a function of time. Use:
x = xosinwt
where xo = the amplitude, (.215 m in this case), and w
we can find from w
= 2pf.
We want sine not cosine as it is starting at the origin as sine does:
w
= 2pf
= 2p(2.0464
Hz ) = 12.86 rad/s = 12.9 rad/s
x = (.215 m)sin((12.9 rad/s)t)
e) and finally, the total energy of the system is the maximum kinetic
energy (which occurs at equilibrium, so there is no potential energy) m = .750
m/s, vmax = 2.76 m/s
total energy = Ek = 1/2mv2
= 2.8566 J = 2.86 J
(Table of contents)
17. <Question goes here>?
What you want to do is compare the equation of motion to our
"template" of it which is in the data packet:
x = xosinwt
where w
= 2pf.
x = (.45 m)cos(8.40s-1t)
don't worry that this equation is cosine, and we have sine, cosine just means
that it started at amplitude, not at equilibrium. Pretty clearly by
comparing the two equations, you can see that
xo = amplitude = .45 m
w
= 8.40 s-1
So already we have answered a), the amplitude is .45 m, duh.
b) To find the frequency, just use:
w
= 2pf.
(w
= 8.40 s-1)
f = 1.336901522 Hz = 1.34 Hz
c) The total energy would be the maximum kinetic energy, so first let's find
the maximum velocity of the mass using:
v = rw
Where r = the amplitude of .45 m, and w
= 8.40 rad/s
v = rw
= 3.78 m/s
and now let's find the total energy using
Total energy = Ek = 1/2mv2
= 3.5721 J = 3.57 J
d) Finally, the kinetic and potential energy when it is at x = .30 m.
I think we need to find the spring constant, so let's use energy:
At amplitude, the
kinetic energy (Ek = 1/2mv2) all turns into elastic potential energy (Eelas
= 1/2ks2),
we know the maximum v = 3.78 m/s, and we know mass (m) and the displacement
(s) as well. Set them equal, and solve for k:
1/2mv2 = 1/2ks2
mv2 = ks2
k =
mv2/s2 =
35.28 N/m
And now we can do the energy thing. At a displacement of .30 m,
the potential energy (Eelas
= 1/2ks2), is
Eelas
= 1/2ks2 = 1.5876 J =
1.6 J
Since the total energy is 3.57 J, and 1.5876 J of it is in potential,
that leaves 3.57 - 1.5876 J = 1.9824 J = 2.0 J as
kinetic.
(Table of contents)
18. <Question goes here>?
This is almost the same as 17
m = 400 g = .400 kg
What you want to do is compare the equation of motion to our
"template" of it which is in the data packet:
x = xosinwt
where w
= 2pf.
x = (.35 m)sin(5.50s-1t)
don't worry that this equation is cosine, and we have sine, cosine just means
that it started at amplitude, not at equilibrium. Pretty clearly by
comparing the two equations, you can see that
xo = amplitude = .35 m
w
= 5.50 s-1
So already we have answered a), the amplitude is .35 m, duh.
b) To find the frequency, just use:
w
= 2pf.
(w
= 5.50 s-1)
f = 0.875352187 Hz = .875 Hz
c) The period would be the inverse of the frequency:
f = 1/T, so T = 1/f = 1.1424 Hz = 1.14 Hz
c) The total energy would be the maximum kinetic energy, so first let's find
the maximum velocity of the mass using:
v = rw
Where r = the amplitude of .35 m, and w
= 5.50 rad/s
v = rw
= 1.925 m/s
and now let's find the total energy using the velocity above, and the given
mass of .400 kg:
Total energy = Ek = 1/2mv2
= 0.7411 J = .741 J
d) Finally, the kinetic and potential energy when it is at x = 10 cm = .10 m.
I think we need to find the spring constant, so let's use energy:
At amplitude (s = .35 m), the
kinetic energy (Ek = 1/2mv2) all turns into elastic potential energy (Eelas
= 1/2ks2),
we know the maximum v = 1.925 m/s, and we know mass (m = .400 kg) and the displacement
(s = .35 m) as well. Set them equal, and solve for k:
1/2mv2 = 1/2ks2
mv2 = ks2
k =
mv2/s2 =
12.1 N/m
And now we can do the energy thing. At a displacement of .10 m,
the potential energy (Eelas
= 1/2ks2), is
Eelas
= 1/2ks2
= 0.0605 J = .061 J
Since the total energy is 0.7411 J, and 0.0605 J
of it is in potential, that leaves 0.7411 J - 0.0605 J =
0.680625 J = .68 J as kinetic.
A graph of it looks like:
(Table of contents)
19. <Question goes here>?
Let's start with this equation of motion
x = xosinwt
where w
= 2pf.
xo is the amplitude, which is given as 28 cm or .28 m, so we are off to a good
start:
x = (.28 m)sinwt
where w
= 2pf.
And now we must find the angular velocity of the system:
w
= 2pf
f = 1/T
and finally
T = 2p Öm/k
so let's not put numbers in and see what happens:
w
= 2pf
= 2p/T
w
= 2p/T
= 2p/(2p Öm/k)
= 1/(Öm/k)
= Ök/m
Which we could have figured out from comparing these two formulas:
a = -k/mx = -w2x,
this implies that w
= Ök/m
as well.
we know that k = 210 N/m, and m = .250 kg, so
w
= Ök/m
w
= 28.98275349 rad/s = 29 rad/s
So our formula becomes
x = xosinwt
x = (.28 m)sin(29s-1
t)
The system has a period of
T = 2p Öm/k
m = .25 kg, k = 210 N/m so T = 0.21679 s.
Since it is a sine wave, it reaches its maximum height at a quarter the period
later:
t = 0.21679/4 = .0541 s, and every .217 seconds thereafter (0.271 s,
0.488 s, 0.705 s 0.921 s)
It reaches its first minimum at 3/4 a period from the beginning:
t = 0.21679(3/4) = .163 s, and every .217 s thereafter (0.163 s, 0.379 s,
0.596 s, 0.813 s 1.03 s)
(Table of contents)
21. <Question goes here>?
This is one of those crazy bullet hitting mass on a spring
problems. I think what happens is
1. the bullet hits the mass, and momentum is conserved
2. the bullet mass system vibrates in SHM with an amplitude of 21.5 cm or .215
m.
This is essentially just like the ballistic pendulum lab, only instead of the
target gaining gravitational potential energy, it gains elastic:
Eelas = 1/2ks2
So the energy it gains is (s = .125 m, k = 6700 N/m)
Eelas = 1/2ks2
= 154.85 J
Right after the collision, this energy was all kinetic, so (m = .600 kg + .025
kg = .625 kg)
Ek = 1/2mv2
(154.85 J) = 1/2(
.625 kg)v2
v = 22.26 m/s which is the post collision velocity of the bullet and the mass
And now we just use conservation of momentum; the momentum of the bullet
before the collision is equal to the momentum of the bullet and mass after:
(.025 kg)v = (.625 kg)(22.26 m/s)
v = 556.5137015 = 557 m/s
(Table of contents)
26. <Question goes here>?
Well, hmmm let's figure out what we do know:
since they reach the lowest point 8 more times in 34.7 seconds, then we know
the period to be
T = 34.7/8 = 4.3375 s which is probably useful
We know the person's mass is 65.0 kg, also useful, since now we can use the
formulas which relates spring constant, mass and period: (T = 4.3375 s, m =
65.0 kg)
T = 2p Öm/k
k = 136.4 N/m
With this spring constant, the spring is stretched by the weight of the
person:
F = ma
wt = (65.0 kg)(9.8 N/kg) = 637 N
and the stretch length can be found using
F = -kx (k = 136.4 N/m, F = 637 N)
x = 4.67 m, which means if it is now 25 m long, then it originally was 25 m -
4.67 m 20.32 m
(why was that a level III???)
(Table of contents)
28. <Question goes here>?
The period is the time per cycle, so it is
T = (50 s)/(36 cycles) = 1.39 s/cycle
The frequency is the cycles per second, so it is
f = (36 cycles)/(50 s) = .72 cycles/sec or .72 Hz
(Table of contents)
29. <Question goes here>?
I assume the period is tick and tock = 2.0 s (I will
tock about this later)
To find the length, use the formula
T = 2p Öl/g
(T = 2.0 s, g = 9.80 m/s/s)
l = .993 m.
Since the length is in the numerator, if it is not otherwise obvious to you,
the period would lengthen with increased length.
(Table of contents)
S1. A spring makes 12 vibrations in 40s. Find the period
and frequency of the vibration.
It's very simple to calculate the period and the frequency of the vibration
by using these formulas:
T = (40 s)/(12 cycles) = 3.333 s/cycle
f = 1/T = (12 cycles)/(40 s) = 0.3 cycles/s = .3 Hz
(Table of contents)
S2. A 50-g mass hangs at the end of a Hookean spring. When
20g more are added to the end of the spring, it stretches 5.0cm more. (a) Find
the spring constant. (b) If the 20g are now removed, what will be the period of
the motion?
Hookean just means that the relationship F = -kx is valid.
(a) We have: F = -kx, and F = ma where a is g, so setting the forces equal:
kx = mg
<=> k = mg/x
= (0.02kg)(9.8m/s/s)/(0.07 m) = 2.8 N/m
(b) T = 2p(m/k)1/2
= 2p(0.05/2.8)1/2 = 0.84s
(Table of contents)
S3. A spring is stretched 4cm when a mass of 50g is hung
on it. If a total 150g is hung on the spring and the mass is started in a
vertical oscillation, what will be the period of oscillation be?
(a) We have: F = -kx, and F = ma where a is g, so setting the forces equal: kx = mg
<=> k = mg/x = (0.05 m)(9.8 m/s/s)/(0.04 m) = 12.25N/m
When the 150g mass is hung on the spring, the
period of the oscillation will be: T = 2p(m/k)1/2
= 2p(0.15/12.25)1/2 = 0.7s
(Table of contents)
S4. A body of weight 27N hangs on a long spring of such
stiffness that an extra force of 9N stretches the spring 0.05m. If the body is
pulled down and released, what is its period?
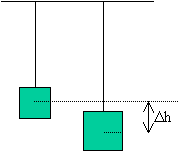
At the balance point as soon as the 9N force stopped stretching the spring: F =
-kx <=> k = F/h
= (9 N)/(0.05m) = 180N/m
The period is now easily to find when we already know the spring constant:
F = ma, m = F/a:
m = (27 N)/(9.8 m/s/s) = 2.76 kg
T = 2p(m/k)1/2
= 2p(2.76/180)1/2 = 0.78 s
(Table of contents)
S7. A 0.5-kg performs simple harmonic motion with a
frequency of 2Hz and an amplitude of 8mm. Find the maximum velocity of the body,
its maximum acceleration, and the maximum restoring force to which the body is
subjected.
Using the tangential velocity as the maximum velocity:
v = rw
And the formula
w = 2pf
vmax = wA = 2pfA = 2p(2.0
Hz)(0.008 m) = 0.1m/s
The maximum acceleration is the centripetal acceleration of the mass moving in
a circle of radius equal to the amplitude:
a = rw2
=> amax = Aw2 = (2pf)2A
= (2p(2.0 Hz))2 (0.008 m) = 1.26m/s2
The restoring force gets its maximum value the acceleration is at its
maximum:
F = ma = (.50 kg)(1.26 m/s/s) = .632 N
(Table of contents)
S8. A mass of 250g hangs on a spring and oscillates
vertically with a period of 1.1s. To double the period, what mass must be added
to the 250g? (Ignore the mass of the spring)
The initial period of the spring is:
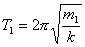
The final period of the spring is:
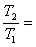 2
2
T2 = 2T1
Now, let’s do one more interesting step here. We will divide T1
by T2
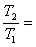
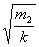
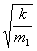
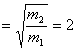
Now, we square both sides, we have:
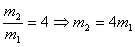
Here we go! At present, we’ve already got the final resolution for the
problem. The last thing is to substitute the number into the formula. Is that
neat? We don’t even have to use the initial period 1.1s.
m2 = 4 x 250 = 1000g = 1kg.
But it’s not all. We need how much mass needed to add into the 250g mass.
Thus we will need: 1000 – 250 = 750g.
(Table of contents)
S9. A body describing SHM (simple harmonic motion) has a maximum acceleration of
8pm/s2 and a maximum speed of 1.6m/s. Find the period T and the
amplitude R.
The
maximum acceleration is the centripetal acceleration of the mass moving in a
circle of radius equal to the amplitude:
a = rw2
Therefore, amax = Aw2
where A is the amplitude of motion
=> amax = Aw2
= 8pm/s2
=> A = 8p/w2
(1)
Using the tangential velocity as the maximum velocity:
v = rw
=> vmax = Aw
= 1.6m/s
(2)
From (1) and (2), we have:
A = 8p/w2
and
Aw
= 1.6m/s
Two equations, and two unknowns
From the first equation, A = 1.6/w
and A is also = 8p/w2
1.6/w
=
8p/w2
1.6
=
8p/w
w
= 8p/1.6
= 15.71 rad/s, so the period would be one revolution (2p)
divided by this:
T = (2p)(1.6)/(8p)
= .4 s
And we will use the relationship
Aw
= 1.6m/s to find A:
A
= ( 1.6m/s)/w
A
= (1.6)/(8p/1.6)
= (1.6)2/(8p)
= .102
m
(Table of contents)