Problem Set 9: Ch4: 31 | 44 | 56 | Ch8: 30 | 31 | Ch9: 1 | 4 | 5 | 6 | 10 | 11 | 12 | 13 | 16 | 17 | 20 | 22 | 25 | 26 | 27 | 31 | Go up
 - by Chris Murray, Julia Scanlon, and Brad Hamlin Fall 2002

Chapter 4:

31. A 6500-kg helicopter accelerates upward at 0.60 m/s² while lifting a 1200-kg car.  (a) What is the lift force exerted by the air on the rotors?  (b) What is the tension in the cable (ignore its mass) that connects the car to the helicopter?

a)
The total mass that is accelerating at .60 m/s/s is the helicopter mass (6500 kg) and the car's mass of 1200 kg or 7700 kg.
The total weight would be: (7700 kg)(9.80 N/kg) = 75460 N down (-) and an unknown force by the air on the rotors (F) with an upward (+) acceleration of .60 m/s/s.  F = ma looks like:
<F - 75460 N> = (7700 kg)(.60 m/s/s), F = 80080 N upwards = 8.0 x 10⁴ N up
b)
The tension in the cable is affected by the car's mass, so looking at the 1200 kg car we have this situation:
The total weight would be: (1200 kg)(9.80 N/kg) = 11760 N down (-) the tension in the cable upward (T) with an upward (+) acceleration of .60 m/s/s.  F = ma looks like:
<T - 11760 N> = (1200 kg)(.60 m/s/s), F = 12480 N upwards = 1.2 x 10⁴ N up
(Table of contents)

44. A box is given a push so that it slides across the floor.  How far will it go, given that the coefficient of kinetic friction is 0.20 and the push imparts an initial speed of 4.0 m/s?

As it slides across the level floor, the only force acting on it horizontally is the force of friction:
F_fr = m_kF_n

Now, the normal force is just the weight of the box since this floor is level, which is F = ma, F_N = mg, where g is the acceleration of gravity.

The force of friction is then
F_fr = m_kF_n = m_k(mg)=  (.20)m(9.8 m/s/s)

Since this is the only force horizontally, the horizontal acceleration is:
F = ma
F = (.20)m(9.8 m/s/s)

So
ma = (.20)m(9.80 m/s/s)
a = (.20)(9.80 m/s/s) = 1.96 m/s/s

Now we have a cute chapter 1 problem to solve:
s = ?, u = 4.0 m/s, v = 0, a = -1.96 m/s/s, t = ?

So find s, use

v² = u² + 2as

s = 4.08 m = 4.1 m
(Table of contents)

56.An 18.0-kg box is released on a 37.0^o incline and accelerates down the incline at 0.270m/s².  Find the friction force impeding its motion.  How large is the coefficient of friction? 

The weight of the box is (18 kg)(9.80 N/kg) = 176.4 N
The component of the weight parallel to the plane is
(176.4 N)sin(37.0^o) = 106.16 N
The component of the weight perpendicular to the plane is
(176.4 N)cos(37.0^o) = 140.88 N
So now our expression of Newton's second law has the parallel component of gravity of 106.16 N down (-) the plane, and assuming it is moving down the plane as well as accelerating down the plane, the force of friction F is acting up (+) the plane, and the acceleration is .270 m/s/s down (-) the plane, so:
<F - 106.16 N> = (18.0 kg)(-.270 m/s/s)
F = 101.3 N = 101 N, and the coefficient of friction is given by
F_fr = m_kF_n
 The Normal force in this case is the perpendicular component of gravity 140.88 N, so we have:
F_fr = m_kF_n
101.3 N = m_k(140.88 N)
So m_k = .719
(Table of contents)

Chapter 8:

30. A person exerts a force of 45N on the end of a door 84cm wide. What is the magnitude of the torque if the force is exerted (a) perpendicular to the door, and (b) at a 60⁰ angle to the face of the door? 

The formula for torque is:
t = r x F = rFsinq
So for the 60^o angle: 
t = (.84 m)(45 N)sin(60^o) = 32.7 Nm = 33 Nm

If the force is applied at a 90^o angle to the radius, the factor sinq becomes 1, and really the torque is:
t = rF = (.84 m)(45 N) = 37.8 Nm = 38 Nm
(Table of contents)

31. Calculate the net torque about the axle of the wheel shown below. Assume that a friction torque of 0.40 m N opposes the motion.

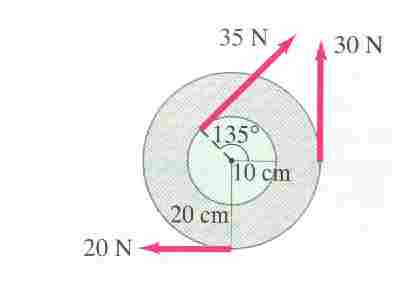
Here we are simply going to add the torques, making CW torques positive, and ACW (Anti Clockwise - it's an IB term) torques negative.  All angels are 90^o so it makes it pretty easy:  (The 135^o angle indicated is not relevant:)
t₃₅ = rF = (.10 m)(35 N) = +3.5 Nm CW
t₃₀ = -rF = -(.20 m)(30 N)  = -6.0 Nm (ACW)
t₂₀ = rF = (.20 m)(20 N)  = +4 Nm CW
Adding all these together:
t = +1.5 Nm CW
But there is a .4 Nm torque opposing the motion, so assuming that the object is rotating CW, then the .40 Nm torque would be acting ACW, and the net torque would be:
t = +1.5 Nm - .40 Nm = 1.1 Nm CW
(Table of contents)

Chapter 9

1. Three forces are applied to a tree sapling, as shown in Fig. 9-47, to stabilize it.  If F₁=282N and F₂=355N, find F₃ in magnitude and direction.

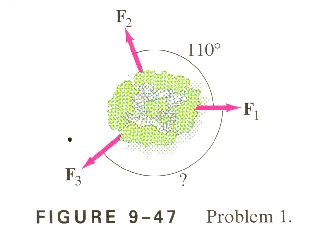
Well, the first thing to do is but F₁ and F₂ in to components:

F₁ is entirely in the +x direction, so it is 282 N x + 0 N y
F₂ is a whole 'nother ball of wax.  yarn.  whatever.
It is (since they give the trigonometric angle)
F₂  = (355 N)cos(110^o) x + (355 N)sin(110^o) y = -121.42 N x +  333.59 N y

Note that the minus sign not only makes sense for the x component, as it would be to the left, but, it just comes from the cosine in this case.

So in the x direction, F₃ has a component F_3x such that:
282 N - 121.42 N + F_3x = 0  (i.e there is no net force as there is no acceleration in the x direction)
And F_3x  = -160.58 N

And, in the y direction, F₃ has a component F_3y such that:
0 N + 333.59 N +  F_3y = 0 (There is no acceleration in the y direction)
So  F_3y = -333.59 N

Now we know that the force F₃ has these components:
 F₃ = -160.58 N x + -333.59 N y

Finally, let's make it into an angle magnitude vector:
Find the magnitude:

hyp = Ö{(160.58 N)² + (333.59 N)²} = 370 N

The angle between the x axis  and the vector  is the inverse tangent of opposite over adjacent:

q =Tan^-1{333.59/160.58} = 64.3^o Below the x axis, and to the left of the y, which means the indicated angle would be 180^o - 64.3^o = 115.7^o = 116^o 
(Table of contents)

4.How far out on a diving board (Fig. 9-48) would a 60-kg diver have to exert a torque of 1000 mN on the board, relative to the left support post? 

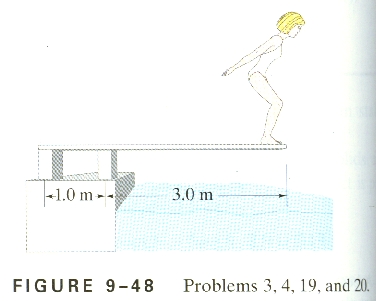
The formula for torque is  t = Fr sinq.  We know that the force exerted by the diver downwards is their weight, F = ma, F = (60 kg)(9.8 N/kg) = 588 N.  The angle here is 90^o, since we assume that the diving board is level, so we can ignore the sine of the angle, so our expression becomes:
t = Fr
1000-mN = (588 N)r, r = 1.7 m, so she would be .7 m beyond the rightmost post.
(Table of contents)

5. Two cords support a chandelier in the manner shown in Fig. 9-6 except that the upper wire makes an angle of 45^o with the ceiling.  If the cords can sustain a force of 1300N without breaking, what is the maximum chandelier weight that can be supported? 

So, pretend the upper angle is 45^o.  Got it???

We know that the chandelier is not necessarily 200 kg either, but some mass such that the maximum tension in the cords is 1300 N.  Let's just set up some equations to see which cord is under the most tension, and then, we'll set that tension to 1300 N>

If we look at the point where the cords come together, you can express the equilibrium of that point as follows:  (The vector sum of F₁, F₂, and F₃ - where  is the weight of the chandelier)

In the x direction:
F_1x + F_2x + F_3x = 0
-F₁cos(45^o)+ F_2x + 0 = 0

So we know that F_2x = F₂ (It has no y component) = F₁cos(45^o)

In the y direction
F_1y + F_2y + F_3y = 0
F₁sin(45^o)+ 0 - weight = 0

So we know that 
F₁ = (weight)/sin(45^o)

And
F₂  = F₁cos(45^o) = ((weight)/sin(45^o))cos(45^o) = weight (since sin(45^o) = cos(45^o))

So F₁ is always going to be larger than F₂ and F₃ which are both equal to the weight, since sin(45^o) is less than one, 
and F₁ = (weight)/sin(45^o)

Now let's solve the problem, making F₁ just equal to 1300 N, as this would be the maximum it could be:


In the x direction:
F_1x + F_2x + F_3x = 0
-(1300 N)cos(45^o)+ F_2x + 0 = 0
-919.24 N + F_2x + 0 = 0

So F_2x = 919.24 N

In the y direction
F_1y + F_2y + F_3y = 0
(1300 N)sin(45^o)+ 0 - weight = 0
919.24 - weight = 0

So the weight is 919.24 N = 920 N
(Table of contents)

6. Calculate the mass m needed in order to suspend the leg shown in Fig. 9-49.  Assume  the leg (with cast) has a mass of 15.0kg, and its CG is 35.0 cm from the hip joint; the sling is 80.5 cm from the hip joint.

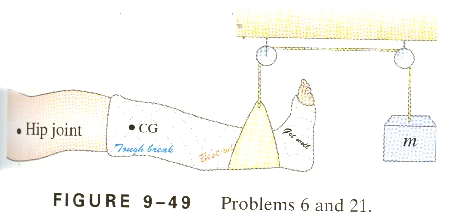
This looks like it will be solvable with torque equilibrium:
If we look at the torques about the hip joint, starting left to right, we have a clockwise (+) torque due to the weight of the leg (= mg = (15.0 kg)(9.8 N/kg) = 147 N) acting at the center of gravity (CG) .350 m from the hip joint of t = Frsinq  = (147 N)(.350 M) = 51.45 Nm, and another counterclockwise (-) torque acting at the sling location .805 m from the hip joint of  t = Frsinq  = (m)(9.8 N/kg)(.805 m) = (7.889Nm/kg)m.  Our torque equilibrium looks like:
<+51.45 Nm - (7.889Nm/kg)m>  = 0
so m = 6.52 kg
(Table of contents)

10.A 70-kg adult sits at one end of a 10-m board, on the other end of which sits his 30-kg child. Where should the pivot be placed so the board (ignore its mass) is balanced? 

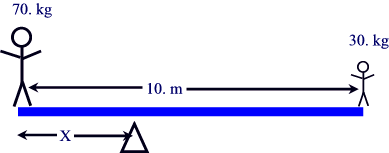
This looks like it is solvable with torque equilibrium:
If we look at the torques about the fulcrum, which is distance x from the adult, the adult is exerting a force of mg = (70. kg)(9.8 N/kg) = 686 N at distance x from the fulcrum, causing an anticlockwise (-) torque of t = Frsinq  = (686 N)x.  The child is exerting a force of mg = (30. kg)(9.8 N/kg) = 294 N at distance (10 m - x) from the fulcrum, causing an clockwise (+) torque of t = Frsinq  = (294 N)(10 m - x).  Our torque equilibrium equation looks like:
<(294 N)(10 m - x) - (686 N)x> = 0
2940 Nm - (294 N)x - (686 N)x = 0
2940 Nm = (980 N)x
x = 3.0 m
(Table of contents)

11. Repeat problem 10 taking into account the board's 15-kg mass. 

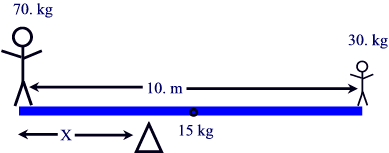
This looks like it is also solvable with torque equilibrium:
If we look at the torques about the fulcrum, which is distance x from the adult, the adult is exerting a force of mg = (70. kg)(9.8 N/kg) = 686 N at distance x from the fulcrum, causing an anticlockwise (-) torque of t = Frsinq = (686 N)x.  The child is exerting a force of mg = (30. kg)(9.8 N/kg) = 294 N at distance (10 m - x) from the fulcrum, causing an clockwise (+) torque of t = Frsinq  = (294 N)(10 m - x).  Finally we have the board itself whose weight of (15 kg)(9.8 N/kg) = 147 N is acting at the center of the seesaw, or at a distance of (5.0 m - x) from the fulcrum, and creating a clockwise (+) torque of t = Frsinq  = (147 N)(5.0 m - x). Our torque equilibrium equation looks like:
<(294 N)(10 m - x) + (147 N)(5.0 m - x) - (686 N)x> = 0
2940 Nm - (294 N)x + 735 Nm - (147 N)x - (686 N)x = 0
2940 Nm + 735 Nm = (294 N)x + (147 N)x + (686 N)x = (1127 N)x
x = 3.26 m from the adult
(Table of contents)

12. Find the tension in the two cords shown in Fig. 9-51.  Neglect the mass of the cords, and assume that the angle is 30^o and the mass m is 200kg

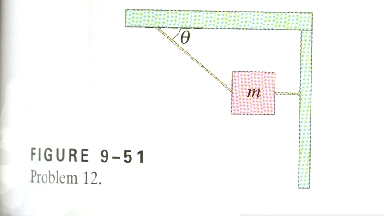
If we ignore any tendency of the box to rotate. (can we?) this is just a force equilibrium problem.
In the horizontal direction, we have a component of the tension of the cord on the left (T_L) of T_Lcos(30^o) acting to the left (-), and the entire tension of the rightmost cord (T_R) acting to right (+).  Our horizontal equilibrium looks like:
T_R - T_Lcos(30^o) = 0
Vertically, the cord on the left has a vertical component T_Lsin(30^o) acting up (+) and the weight of the mass is (200 kg)(9.8 N/kg) = 1960 N down (-):
T_Lsin(30^o) - 1960 N = 0.  This is directly solvable for T_L:
T_L = (1960 N)/sin(30^o) = 3920 N, And now with the first equation we can solve for the right cord:
T_R - T_Lcos(30^o) = 0
T_R = (3920 N)cos(30^o)
T_R = 3394.819583 = 3400 N
(Table of contents)

13. Find the tension in the two wires supporting the traffic light shown in Fig. 9-52.

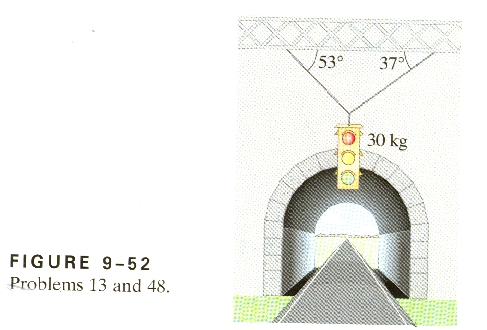
This is a force problem.  So let's go:
Vertical:
We have the weight of the light (30 kg)(9.8 N/kg) = 294 N down (-), and the vertical components of the tensions in the cords.  I will call the leftmost cord T_L and the rightmost T_R. The vertical component of T_L is T_Lsin(53^o), and of T_R, T_Rsin(37^o) and these are both upward (+) so our equilibrium looks like:
 T_Lsin(53^o) + T_Rsin(37^o) - 294 N= 0
Which is not solvable, as it has two unknowns.  So let's set up Horizontal.
In the x direction, we have the horizontal components of the two cords acting in the opposite directions.  The horizontal component of T_L, T_Lcos(53^o), acts to the left (-), and the horizontal component of T_R, T_Rcos(37^o) acts to the right (+) so we have
T_Rcos(37^o) - T_Lcos(53^o) = 0

Which means that 
T_R = T_Lcos(53^o)/cos(37^o)

Popping this into our first equation, we get:
T_Lsin(53^o) + T_Rsin(37^o) - 294 N= 0
T_Lsin(53^o) + {T_Lcos(53^o)/cos(37^o)}sin(37^o) - 294 = 0
So
T_Lsin(53^o) + T_Lcos(53^o)tan(37^o) = 294 N
T_L(sin(53^o) + cos(53^o)tan(37^o)) = 294 N
T_L = (294 N)/(sin(53^o) + cos(53^o)tan(37^o)) = 234.79884 N = 230 N (the book says 240??)
And since
T_R = T_Lcos(53^o)/cos(37^o)
T_R = (234.79884 N)cos(53^o)/cos(37^o) = 176.9336 N = 180 N


But wait - there is a better way to do this.

Since 37^o and 53^o are complementary, we can just set up our coordinate system along the cables....
(Table of contents)

16.A 0.60kg sheet hangs from a massless clothesline as shown in Fig. 9-53.  The line on either side of the sheet makes an angle of 3.5^o with the horizontal.  Calculate the tension in the clothesline on either side of the sheet.  Why is the tension so much greater than the weight of the sheet?

The tension in the clothesline has two vertical components of Tsin(3.5^o) that act upward (+) against the force of gravity (.60 kg)(9.8 N/kg) = 5.88 N acting on the sheet downward (-) so our vertical equation of equilibrium is:
Tsin(3.5^o) + Tsin(3.5^o) - 5.88 N = 0
2Tsin(3.5^o) - 5.88 N = 0
T = (5.88 N)/(2sin(3.5^o)) = 48 N
Since only the vertical components balance the weight, and since the angle is so small, then it takes a great deal of tension so that 2Tsin(3.5^o) = 5.88 N
(Table of contents)

17. A door, 2.30m high and 1.30m wide, has a mass of 13.0kg.  A hinge 0.40m from the top and another hinge 0.40m from the bottom each support half the door's weight (Fig. 9-54).  Assume that the center of gravity is at the geometrical center of the door, and determine the horizontal and vertical force components exerted by each hinge on the door.

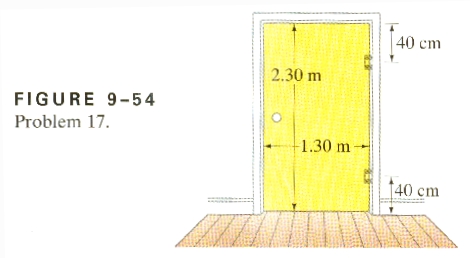
Let's call the force exerted by the upper hinge Upper, and the force exerted by the lower hinge Lower.  For force equilibrium, we know that the horizontal components that the hinges exert must cancel out, as they are the only players acting horizontally.  Let's guess that the upper hinge is exerting a force to the right (+), and the lower is exerting a force to the left (-) on the door, our equilibrium looks like:
Upper_x - Lower_x = 0
Vertically, there is nothing too exciting going on either.  The weight of the door (13.0 kg)(9.8 N/kg) = 127.4 N down (-), and the two hinges lifting up(+) on the door:  (Are they the same?)
Upper_y + Lower_y - 127.4 N = 0
OK - umm  so let's talk about TORQUE!
We need to pick a spot to calculate the torque about, so let's pick the lower right corner of the door.  (it doesn't matter what point you pick)
Hmm, so many forces, so big a door.  Well, the vertical forces exerted by the hinges do not contribute to the torque about the lower right corner of the door, as they are directly away from the pivot point (t = Frsinq, and q = 0^o).  This might be why I chose this point, but then again it might have been a Lucky Guess.  The horizontal components of force exerted by the hinges (Upper_x , Lower_x ) create torque.  If I guess, (as I did before in the force section) that the Lower hinge is pushing to the left, and the upper is to the right, then we have the upper hinge causing a clockwise (+) torque with a force of Upper_x,  acting at a distance of 2.30 m - .40 m = 1.90 m from the lower right corner to create a  torque of +(Upper_x)(1.90 m), and the lower hinge is causing an anticlockwise (-) torque with a force of Lower_x,  acting .40 m away from the lower right corner to create a torque of -(Lower_x)(.40 m).  Hmm, all we have left is the weight.  This gets tricky, or maybe it doesn't:


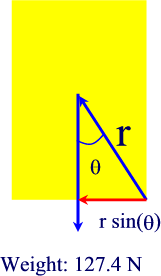
The weight acts at the center of mass, which is the center of the door (we are told), and so in the diagram above, the arrow straight down is the weight of the door (127.4 N)  
since t =  Frsinq, and since rsinq is just half of the width of the door, we don't even need to know r which would have been the distance from the center of the door to the lower right hand corner, as it is only the horizontal part of r that matters.  (Only the horizontal location of the center of mass matters).  The weight, of course, exerts an anti clockwise torque about the lower right corner, and acts at half the width, or 1.3 m / 2 = .65 m, so we have a torque of -(127.4 N)(.65 m) due to the weight.  

So our TOTAL TORQUE EQUILIBRIUM looks like:
+(Upper_x)(1.90 m) - (Lower_x)(.40 m) -(127.4 N)(.65 m) = 0


Time for math

Here are our equations:
Upper_x - Lower_x = 0
Upper_y + Lower_y - 127.4 N = 0
+(Upper_x)(1.90 m) - (Lower_x)(.40 m) -(127.4 N)(.65 m) = 0

Now, we have too many unknowns to be allowed.  (4, with only three equations).  I think it is a fair assumption, that if
Upper_x - Lower_x = 0, then Upper_x = Lower_x = Hinge_x  (as we will now call it), and then we can assume that the door is well built, and that the vertical components exerted by the hinges are identical.  (although I have encountered doors in my life where this is not true :-) 
Upper_y + Lower_y - 127.4 N = 0
So I will assume that Upper_y = Lower_y  = Hinge_y  (as we will now call it)
So now our equations are more manageable:

Upper_x - Lower_x = 0
Upper_y + Lower_y - 127.4 N = 0
+(Upper_x)(1.90 m) - (Lower_x)(.40 m) -(127.4 N)(.65 m) = 0

Becomes

2(Hinge_y) - 127.4 N = 0
+(Hinge_x)(1.90 m) - (Hinge_x)(.40 m) -(127.4 N)(.65 m) = 0

Which makes me smile.
2(Hinge_y) - 127.4 N = 0, so Hinge_y  = 63.7 N

and
+(Hinge_x)(1.90 m) - (Hinge_x)(.40 m) -(127.4 N)(.65 m) = 0
+(Hinge_x)(1.90 m - .40 m)  = 82.81 Nm
Hinge_x = 55.2 N

So both hinges exert an upward force of 63.7 N (assuming they are mounted in the right place) and the top hinge exerts a force to the right of 55.2 N, and the lower hinge exerts a force to the left on the door of 55.2 N
(Table of contents)

20. Calculate the forces F₁ and F₂ that the supports exert on the diving board of Fig. 9-48 when a 60-kg person stands at its tip. Take into account the board's mass of  35kg.  Assume the board's CG is at its center.

Horizontally there is not much going on here, but vertically we have the two unknown forces F₁ and F₂, acting whichever way they act,  the weight of the board (35 kg)(9.8 N/kg) = 343 N down (-), and the weight of the diver (60. kg)(9.8 N/kg) = 588 N down (-) so our force equation looks like:
F₁ + F₂ - 343 N - 588 N = 0

Torque-wise things are busy.  If we use the left side of the board then F₁ generates no torque, as it acts at r = 0 from the left side, assuming that F₂ is upward, it generates an anti-clockwise (-) torque of (F₂)(1.0 m) as it acts at a distance of 1.0 m from the left side, the weight of the board acts at its CG, 2.0 m from the left, and so  generates a clockwise (+) torque of (2.0 m)(343 N), and the diver's weight also generates a clockwise (+) torque, of (4.0 m)(588 N) acting at the very end (4.0 m).  Our torque looks like this:
0 - (F₂)(1.0 m) + (2.0 m)(343 N) + (4.0 m)(588 N) = 0

This is directly solvable for F₂:
(2.0 m)(343 N) + (4.0 m)(588 N) = (F₂)(1.0 m)
F₂ = 3038 N  = 3.0 x10³ N upwards.

And now let's plug into the vertical force equilibrium to solve for F₁:
F₁ + F₂ - 343 N - 588 N = 0
F₁ + 3038 N - 343 N - 588 N = 0
F₁ = -2107 N = -2.1x10³ N (downwards)
(Table of contents) 

22. Calculate F₁ and F₂ for the beam shown in Fig. 9-56.  Assume it is uniform and has a mass of 250kg.

This looks like a force and torque problem.  Let's set up the force equilibrium first.  Nothing is happening in the horizontal direction, but in the vertical direction, we have F₁ and F₂ up (+) and 4000 N, 3000 N, 2000 N and the weight of the beam (250 kg)(9.8 N/kg) = 2450 N down (-), so our force equilibrium in the vertical direction looks like:
F₁ + F₂ - 4000 N - 3000 N - 2000 N - 2450 N = 0
F₁ + F₂ - 11450 N = 0
But alas, we are not done, as this is two unknowns, but only one equation.  So let's set up the torque equation, about the leftmost side of the beam, so that the downward forces of 4000 N , 3000 N and 2000N, as well as the 2450 N weight of the beam (acting in the  center) all contribute clockwise (+) torques, and F₁ contributes no torque as it has a radius of zero, and F₂ contributes an anticlockwise (-) torque.  Our torque equilibrium looks like:  (t = Frsinq)
F₁(0 m) + (4000 N)(2.0 m) + (2450 N)(5.0 m) + (3000 N)(6.0 m) + (2000 N)(9.0 m) - F₂(10.0 m) = 0
F₂ = 5625 N
and since from our first equation said that
F₁ + F₂ - 11450 N = 0
F₁ = 11450 N - F₂ = 11450 N - 5625 N = 5825 N
(Table of contents)

25. A 170-cm-tall person lies on a light (massless) board which is supported by two scales, one under the feet and one beneath the top of the head (Fig. 9-58).  The two scales read, respectively, 31.6 and 35.1kg.  Where is the center of gravity of this person?

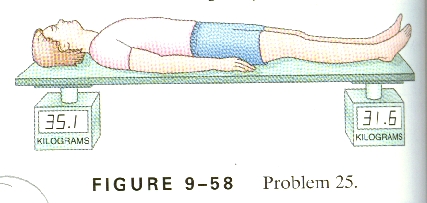
The scales record kilograms, but they are really registering force, the left one is reading 35.1 kg, which means it is exerting an upward force of (35.1 kg)(9.8 N/kg) = 343.98 N, and the rightmost one is reading 31.6 kg, which means it is exerting an upward force of (31.6 kg)(9.8 N/kg) = 309.68 N.  
Now we need to set up the force equation in the vertical direction.  We have the scales exerting upward forces of 343.98 N and 309.68 N, and gravity exerting a downward force equal to the weight of the person  (the board is massless), so our vertical equation of equilibrium looks like:
343.98 N + 309.68 N - weight = 0 where weight is the weight of the person.

Lets talk the torque:
Calculating torque from the left side (why not???), the left scale has nothing to torque about (r = 0) and so the 343.98 N force acts at a distance of 0 from the left side, and therefore creates no torque.  Moving right, we have the weight of the person generating a clockwise (+) torque, but we don't know how far over it acts, so we are left with (t = Frsinq) a torque of +(x)(weight), where x is the distance from the top of the person's head that their center of mass is.  FInally, on the far right side (r = 1.70 m) the rightmost scale exerts an upward force of 309.68 N creating an anticlockwise torque of -(1.70 m)(309.68 N) = -526.456 Nm.  Our Torque equation looks like:
0 + (x)(weight)  -526.456 Nm = 0

MATH time!!!
From the first equation:
343.98 N + 309.68 N - weight = 0
we know that the weight is simply:
343.98 N + 309.68 N = weight = 653.66 N, which we will plug in to our second:
0 + (x)(weight)  -526.456 Nm = 0
(x)(653.66 N) = 526.456 Nm 
x = 0.805 m from the top of their head, and 1.70 m - 0.805 m = .895 m from their feet.
(Table of contents)

26. A shop sign weighing 215 N is supported by a uniform 135 N beam as shown in Fig. 9-59.  Find the tension in the guy wire and the horizontal and vertical forces exerted by the hinge on the beam.

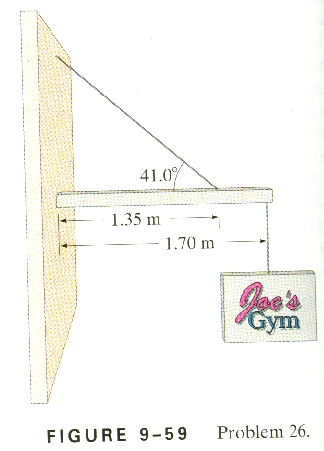
This is a full-sledged torque and two dimensional force equilibrium problem.  Doesn't get too much finer than this.  Grade A USDA all AMERICAN red-blooded, honest to goodness, no nonsense, no joking around, sure's shootin, God fearin' no-holds barred.  OK you get the point.
Hmm.
Well, let's look at the beam, and start with force.  The vertical direction.  The horizontal direction.  No, let's start vertically, not that it much matters much where we start.  DOES ANYONE HAVE ANY IDEA HOW TO SOLVE THIS HERE PROBLEM???

(How 'bout dose Bearss?)

didn't think so.

OK - try to stay calm.  Think.  In the vertical direction we have the weight of the sign (215 N) down (-), the weight of the beam (135 N) down (-), and the wall (W_y) acting umm.  HECK IF I KNOW WHICH WAY THE WALL ACTS IN THE VERTICAL DIRECTION - COULD BE UP, COULD BE DOWN.  guess we'll leave it as a variable.  Oh, the tension in the cable has an upward (+) component Tsin(41.0^o), where T is the tension in the cable.  So our vertical expression looks like:
W_y - 215 N - 135 N + Tsin(41.0^o) = 0
So.  Ho boy. Two unknowns. One equation so far.
Well, horizontally in the force picture we have a component of the cable tension to the left (-) of Tcos(41.0^o), and opposing that to the right (+) the wall pushing to the right with a force of W_x.  That looks like:
W_x - Tcos(41.0^o) = 0
Great.  Just great.  Another unknown.
Well, on to torque.
From the left side of the beam, (So W_y acts at r = 0) we have the weight of the beam (135 N) acting at the center (.85 m from the left) of the beam, and the weight of the sign (215 N)  acting at the end (1.70 m) both creating a clockwise (+) torque, and the vertical component of the tension (Tsin(41.0^o)) acting at 1.35 m from the left creating an anticlockwise (-) torque:
W_y(0 m) + (135 N)(.85 m) - (Tsin(41.0^o))(1.35 m) + (215 N)(1.70 m) = 0
WELL,  TORQUE ABOUT EASY!!! - uh that is one equation and one unknown.
0 + 114.75 Nm - (Tsin(41.0^o))(1.35 m) + 365.5 Nm = 0
T = 542.24 N = 542 N

WOO HOO!
The rest is easy.  Let's just sweep up the pieces.  To find the horizontal component of the force the wall exerts (W_x) we'll use our second equation:
W_x - Tcos(41.0^o) = 0
W_x =  (542.24 N)cos(41.0^o) = 409 N

And to find the vertical component (W_y) let's use the very first equation we made:
W_y - 215 N - 135 N + Tsin(41.0^o) = 0
W_y = 215 N + 135 N - (542.24 N)sin(41.0^o) = -5.74 N - So it was down after all.
(Table of contents)

27. A traffic light hangs from a structure as shown in Fig. 9-60. The uniform aluminum pole AB is 7.5m long and has a mass of 8.0kg.  The mass of the traffic light is 12.0kg.  Determine the tension in the horizontal massless cable CD, and the vertical and horizontal components of the force exerted by the pivot A on the aluminum pole.

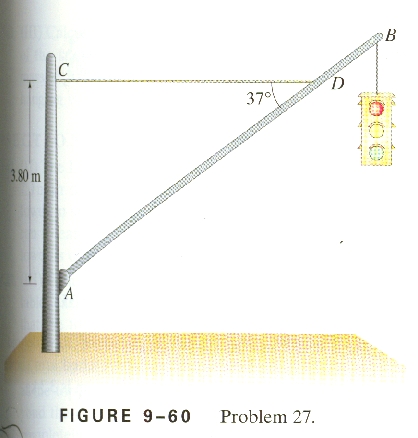
A bit of geometry or trig, the pole is 7.5 m long, but the cable is attached, hmm sin(37^o) = (3.80 m)/hyp, so hyp = (3.80 m)/sin(37^o) = 6.314 m from the bottom of the pole.

Force vertical:
Pole weight = (8.0 kg)(9.8 N/kg) = 78.4 N down
Signal weight = (12 kg)(9.8 N/kg) = 117.6 N down
Pivot at pt A = P_y
Equilibrium:
P_y - 78.4 N - 117.6 N = 0

Force Horizontal:
Cable = T (left)
Pivot at point A =  P_x (right)
Equilibrium:
P_x - T = 0



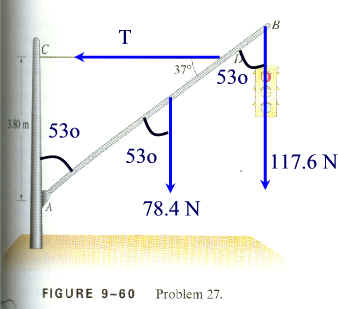
Torque about the bottom point (point A)
The pivot acts at r = 0 so exerts no torque, so that leaves us the weight of the beam of 78.4 N acting in the middle (at 7.5/2 = 3.75 m from point A), the tension (T) of the cable acting at 6.314 m from point A, and the weight of the signal (117.6 N) acting at 7.5 m from point A.  Notice that the downward forces act at a complementary angle (53^o) with the angle the tension makes.
  t =  Frsinq,
Pole: +(78.4 N)(3.75 m)sin(53^o) (CW)
Signal: +(117.6 N)(7.5 m)sin(53^o) (CW)
Cable: -T(6.314 m)

And or course, all this rot adds to zero:
+(78.4 N)(3.75 m)sin(53^o) + (117.6 N)(7.5 m)sin(53^o) - T(6.314 m)sin(37^o) = 0
234.8 + 704.4 - T(6.314 m)sin(37^o) = 0
T = 247.16 N = 250 N

BUT - we're not done.  We still need to figure out the force exerted by the pivot in the vertical and horizontal direction.  These two formulas will help:

P_y - 78.4 N - 117.6 N = 0, so P_y = 196 N
P_x - T = 0, so P_y= T =  250 N
(Table of contents)

31. Consider again the ladder of Example 9-9 but with a painter climbing up.  If the mass of the ladder is 12.0kg, the mass of the painter is 60.0kg, and the ladder begins to slip at its base when she is 70 percent of the way up the length of the ladder, what is the coefficient of static friction between the ladder and the floor?  Again assume the wall is frictionless.  A free-body diagram is shown in Fig. 9-63.

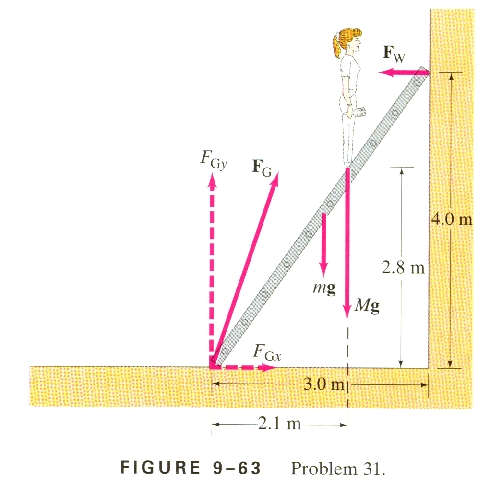
We know at the point of slipping that F_Gx (See diagram above) is just equal to the friction force, where the normal force is F_Gy (The upward force exerted by the ground on the ladder - see diagram above.)  
So, applying the formula for friction:
F_fr = m_sF_n (at the point of slipping)
F_Gx = m_sF_Gy
so
m_s = F_Gx/F_Gy

So, let's set up our equations.

Vertical Force:
Ladder weight: -(12.0 kg)(9.8 N/kg) = -117.6 N (down)
Person weight: -(60.0 kg)(9.8 N/kg) = -588 N (down)
Ground pushing up: +F_Gy (up)
Equilibrium:
F_Gy -117.6 N - 588 N = 0

Horizontal Force:
Force exerted by the wall: -F_W (left)
Force exerted by the ground horizontally: +F_Gx (right)
Equilibrium:
+F_Gx + -F_W = 0

And finally torque:
First, the ladder is at an angle of Tan^-1(3/4) = 36.87^o with the wall, the ladder is 5.0 m long, (5² = 3² + 4²), and the person is 3.5 m (70% of 5) from the bottom.  We then have the following torques about the bottom of the ladder:
The ground: torque = 0 (r = 0)
The weight of the ladder: 117.6 N at an angle of 36.87^o at a distance of 5/2 = 2.5 m from the bottom of the ladder. Torque = (2.5 m)(117.6 N)sin(36.87^o) = + 176.4 Nm (CW)
The weight of the person on the ladder: 588 N at an angle of 36.87^o at a distance of 3.5 m from the bottom of the ladder. Torque = (3.5 m)(588 N)sin(36.87^o) = + 1234.8 Nm (CW) 
The wall pushing to the left: F_W (an unknown component) acting at a distance of 5.0 m from the bottom, at an angle of 90^o - 36.87^o = 53.13^o with the ladder. Torque = -(5.0 m)F_Wsin(53.13^o)  (ACW)
Equilibrium:
0 + + 176.4 Nm + 1234.8 Nm - (5.0 m)F_Wsin(53.13^o) = 0
Which yippee skippee is solvable for F_W.
F_W = 352.8 N

Using our vertical equation:
+F_Gx + -F_W = 0, it is clear that F_Gx also is equal to 352.8 N

And finally, the vertical equation is solvable as well:
F_Gy -117.6 N - 588 N = 0
F_Gy = 705.6 N, and finally, to find the friction:

F_fr = m_sF_n (at the point of slipping)
F_Gx = m_sF_Gy
so
m_s = F_Gx/F_Gy = (352.8 N)/(705.6 N) = .50 - am I done yet?
(Table of contents)