Problem Set 8.9: | 11
| 12 | 17 | 23 | 26
| 27 | 30 |
32 | 33 | 35 | 38
| 40 | 42 | 46 | 48
| 53 | 54 | 55 | 59
| 60 | 65 | 66 | 69
| 80 | Go up
- by Sonja Scherer, To Chong, and Chris Murray, 2002
11. A child rolls a ball on a lever floor 4.5m to another
child. If the ball makes 15.0 revolutions, what is its diameter?
Here we use the tangential relationship
between the tangential displacement, angle and radius:
s
= rq
But first we need the angle in radians:
(15.0 revolutions)(2p
radians/rev) = 94.25 radians
Finally:
s
= rq
4.5 m = r(94.25 radians)
r = 0.047746483 m, but they wanted diameter (TRICKY!!!!!!!), so double this
diameter = 0.0955 m
(Table of contents)
12. A bicycle with
68-cm-diameter tires travels 7.0km. How many revolutions do the wheels
make?
Here we use the tangential relationship
between the tangential displacement, angle and radius:
s
= rq
: r = .68/2 = .34 m, s = 7000 m
q
= (20588.23529 radians)(rev/2p
radians) = 3276.7 rev = 3300 rev
(Table of contents)
17. A 70-cm-diameter wheel
accelerates uniformly from 160rpm to 280rpm in 4.0s. Determine (a) its angular acceleration,
and (b) the radial and tangential components of the linear acceleration of the
point on the edge of the wheel 2.0s after it has started accelerating?
wo
= (160 Revolutions/Minute)(2p
radians/revolution)(1 minute/60 sec) = 16.76 rad/s
w
= (280 Revolutions/Minute)(2p
radians/revolution)(1 minute/60 sec) = 29.32 rad/s
t = 4.0 s
r = (.70 m)/2 = .35 m
Now apply:
w =
wo + at
a
= 3.1416 rad/s/s = 3.1 rad/s/s
The tangential acceleration is uniform throughout the interval, and given by
the tangential relationship:
a = ar=
(3.1416 rad/s/s)( .35 m)
= 1.1 m/s/s
Since the centripetal acceleration depends on the angular velocity, and that
changes throughout the interval, we need to find what the angular velocity is
at t = 2.0 s
w = wo + at
w =
16.76 rad/s
+ (3.1416 rad/s/s)(2.0
s) = 23.03834613 rad/s
And now use centripetal acceleration:
a = rw2
= (.35 m)(23.03834613 rad/s)2 = 185.7678873 = 190
m/s/s of radial or centripetal acceleration
(Table of contents)
23. Pilots can be tested for
the stress of flying high-speed jets in a whirling "human centrifuge"
which takes 1.0 min to turn through 20 complete revolutions before reaching its
final speed. (a) What was its angular acceleration (assume constant), and (b)
what was its final speed in rpm?
Another cute kinematics question.
q
= (20. rev)(2p
radians/rev) = 125.7 radians
t = 1.0 min = 60. sec
wo
= 0
I am going to choose
q = wot
+ 1/2at2
:q
= 125.7 radians; t = 60 s;wo
= 0
a
= 0.070 rad/s/s
For the final velocity, I could use
w = wo + at
But that is not my favorite way to do it, and besides, I would have to use the
answer I got previously, which could be wrong, so I will use my favorite
kinematic formula:
s = (u+v)t/2
Which is this translated in to angular form:
q
= (wo+w)t/2
:
wo
= 0; t = 60 s; q
= 125.7 radians
w
= (4.188790205rad/s)(revolution/2p
rad)(60 sec/min) = 40 RPM
So it came out even???? What if we did not turn everything into radians
and left it in minutes and revolutions:
q
= (wo+w)t/2
:
wo
= 0; t = 1.0 min; q
= 20 rev
w
= 2q/t
= 2(20 rev)/(1 min) = 40 rev/min = 40 RPM slick. You can save time by
using original units sometimes
(Table of contents)
26. A small rubber wheel is used to drive a large pottery
wheel, and they are mounted so that their circular edges touch. If the small
wheel has the radius of 2.0cm and the accelerates at the rate of 7.2rad/s2
, and it is in contact with the pottery wheel (radius 25.0cm) without slipping,
calculate (a) the angular acceleration of the pottery wheel, and (b) the type it
takes the pottery wheel to reach its required speed of 65rpm.
Since the wheels touch, they share tangential everything,
(if they do not slip). They have the same tangential displacement,
velocity, and acceleration:

Since the tangential accelerations are the same, and given
by:
a = ra
Then we can say that if a1 = a2 , then
r1a1
= r2a2
So for our 2.0 cm driving wheel with an angular acceleration of 7.2 rad/s/s,
and the 25.0 cm pottery wheel:
(.020 m)(7.2 rad/s/s) = (.25 m)a2
a2
= 0.576 rad/s/s
Now we just have a cute kinematics problem to solve:
wo
= (65 Revolutions/Minute)(2p
radians/revolution)(1 minute/60 sec) = 6.807 rad/s
w
= 0
a
= 0.576 rad/s/s
To find time, use:
w = wo + at
: wo
= 6.807 rad/s; w
= 0;
a
= 0.576 rad/s/s
t = 11.8 s = 12 s
(Table of contents)
27. The tires of a car make 65 revolutions as the car
reduces its speed uniformly from 100km/h to 50km/h. The tires have the diameter
of 0.80m. (a) What was the angular acceleration? (b) If the car continues to
decelerate at this rate, how much more time is required for it to stop?
First - get rid of km/h:
u = (100 km/hr)(1 m/s/3.6km/hr) = 27.78 m/s
v = (50 km/hr)(1 m/s/3.6km/hr) = 13.89 m/s
And they give you the Diameter, and we'd better use the radius
r = dia/2 = .80 m/2 = .40 m
Now we can use the tangential velocity relationship to find the wo
and w:
v = rw
so w
= v/r
wo
= u/r = (27.78 m/s)/(.40 m) = 69.44 rad/s
w
= v/r = (13.89 m/s)/(.40 m) = 34.72 rad/s
q
= (65 rev)(2p
radians/rev) = 408.41 radians
Now we can find the angular acceleration (deceleration?) with:
w2 = wo2
+ 2aq
: wo = 69.44 rad/s; w
= 34.72 rad/s; q
= 408.41 radians
a
= -4.4281 rad/s/s
To find the additional time required to bring the car to a halt, we just solve
another kinematics problem. Since we already have the angular
deceleration, and since when the angular velocity of the wheels of the car is
zero, the linear velocity is also zero (if the car does not skid) then we can
just solve to the time required to get to zero angular velocity. So for 34.72
rad/s to zero:
wo
= 34.72 rad/s
w
= 0
a
= -4.4281 rad/s/s
To find time, use:
w = wo + at
t = 7.841 s = 7.8 s
(Table of contents)
30. A person exerts a force of 45N on the end of a door
84cm wide. What is the magnitude of the torque if the force is exerted (a)
perpendicular to the door, and (b) at a 600 angle to the face of the
door?
The formula for torque is:
t = r
x F = rFsinq
So for the 60o angle:
t
= (.84 m)(45 N)sin(60o)
= 32.7 Nm = 33 Nm
If the force is applied at a 90o
angle to the radius, the factor sinq
becomes 1, and really the torque is:
t = rF
= (.84 m)(45 N) = 37.8 Nm = 38 Nm
(Table of contents)
32. If the coefficient of static friction between tires
and pavement is 0.75, calculate the minimum torque that must be applied to the
66-cm-diameter tire of a 1080kg automobile in order to "lay rubber"
(make the wheel spin, slipping as the car accelerates). Assume each tire
supports an equal share of the weight.
If each wheel supports an equal share of the weight, then
F = ma
F = (1080 kg)(9.80 N/kg) = 10584 N is divided into four equal parts, so the
normal force at each tire is
FN = (10584 N)/4 = 2646 N
This means that the maximum static force of friction tangential to the drive
wheels must be:
Ffr =
µsFN
= (.75)(2646 N) = 1984.5 N
The formula for torque is:
t = r
x F = rFsinq
Since the road must be tangential to the tire, the force is applied at a 90o
angle to the radius, so the factor sinq
becomes 1, and really the torque is:
t = rF
= (.33 m)(1984.5 N) = 654.9 Nm = 650 Nm
(They gave you the diameter - .66 m diameter, .33m radius)
(Table of contents)
33.
The bolts on the cylinder head of an engine require tightening to a torque
of 80m.N. If a wrench is 30cm long, what force perpendicular to the wrench must
the mechanic exert at its end? If the six-sided bolt head is 15mm in diameter,
estimate the force applied near each of the six points by a rocket wrench.
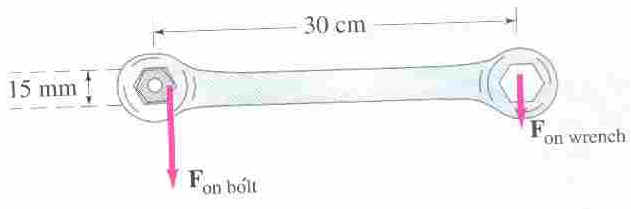
The formula for torque is:
t = r
x F = rFsinq
Since force is applied at a 90o
angle to the radius, so the factor sinq
becomes 1, and really the torque is:
t = rF
t
= 80 Nm
r = .30 m
F = (80 Nm)/(.30 m) = 266.67 N,
This force is much greater at the locale of the bolt head itself, with a
diameter of 15 mm, or radius of 7.5 mm:
t = rF
t
= 80 Nm
r = 7.5x10-3 m
F = (80 Nm)/(7.5x10-3 m) = 10666.7 N, which divided
by the six sides is:
F = 1777.8 N = 1800 N per side
(Table of contents)
35. Calculate the moment of inertia of a 66.7cm-diameter
bicycle wheel. The rim and tire have a combined mass of 1.25kg. The mass of the
hub can be ignored (why?).
The moments of inertia are listed on p. 223, and a thin hoop
through its center is:
I =
mr2
m = 1.25 kg
r = (.667 m)/2 = .3335 m (They gave you the diameter)
so
I =
(1.25 kg)(.3335 m)2 =
1.16 kgm2 = the book gives 1.39 as the answer - but I think it is
wrong.....
Because the distance from the center is so small for the hub, its mass can be
ignored. One might wonder how you could easily mass just the rim and
tire....
(Table of contents)
38.A small 1.05kg ball on the end of the light rod is
rotated in a horizontal circle of a radius 0.900 m. Calculate (a) the moment of
inertia of the system about the axis of rotation, and (b) the torque needed to
keep the ball rotating at a constant angular velocity if air resistance exerts a
force of 0.0800N on the ball.
I think "light" is a code word for massless. (If this makes
you angry - try not to Coop up your anger - just let it out!!!)
A mass on a stick has the same moment of inertia as a thin hoop:
I =
mr2
I =
(1.05 kg)(.900)2 = 0.8505 kgm2
If the mass is moving at a constant angular velocity, then it is not
accelerating, and the only necessary torque merely cancels out the torque
applied by the frictional force of .0800 N acting at a radius of .900 m on the
ball:
Since force is applied at a 90o
angle to the radius, so the factor
sinq
becomes 1, and really the torque is:
t = (.0800
N)(.900 m) = .072 Nm
(Table of contents)
40. A grinding wheel is a uniform cylinder with a radius
of 8.5cm and a mass of 0.580kg. Calculate (a) its moment of inertia about its
center, and (b) the applied torque needed to accelerate it from rest to 1500rpm
in 5.00s if it is known to slow down from 1500rpm to rest in 55.0s.
The moments of inertia are listed on p. 223, and a uniform
cylinder through its center is:
I =
1/2mr2
so
I =
1/2(.580 kg)(.0850 m)2 =
0.00209525 kgm2
Now, if it slows down from 1500 RPM to rest, there must be a frictional torque
present, so let's figure that out first:
To go from 1500 RPM to rest in 55.0 s:
wo
= (1500 Revolutions/Minute)(2p
radians/revolution)(1 minute/60 sec) = 157.08 rad/s
w
= 0
t = 55.0 s
Now apply:
w =
wo + at
a
= -2.856 rad/s/s
And finally the angular equivalent of F = ma:
t =
Ia
t
= (0.00209525 kgm2)(-2.856
rad/s/s) = -0.005984 Nm of frictional torque
To go from rest to 1500 RPM in 5.00 s:
wo
= 0
w
= (1500 Revolutions/Minute)(2p
radians/revolution)(1 minute/60 sec) = 157.08 rad/s
t = 5.00 s
Now apply:
w =
wo + at
a
= 31.41592654 rad/s/s
And finally the angular equivalent of F = ma, but this time we have
more than one torque, we have the unknown torque which I will make positive,
and a frictional torque of -0.005984 Nm
acting counter to this, which I will make negative:
t =
Ia
<t
-0.005984 Nm> = (0.00209525 kgm2)(31.41592654
rad/s/s)
t
= 0.06582 Nm + 0.005984 Nm = 0.0718
Nm
(Table of contents)
42. A day-care worker pushes tangentially on a small
hand-driven merry-go-round and is able to accelerate it from rest to a spinning
rate of 20rpm in 10.0s. Assume the merry-go-round is a disk of a radius 2.5m and
has a mass of 800kg, and two children (each with a mass of 25 kg) sit opposite
each other on the edge. Calculate the torque required to produce the
acceleration, neglecting frictional torque. What force is required?
wo
= 0
w
= (20 Revolutions/Minute)(2p
radians/revolution)(1 minute/60 sec) = 2.0944 rad/s
t = 10.0 s
The moments of inertia are listed on p. 223, and a uniform
cylinder through its center is:
I =
1/2mr2
so
I =
1/2(800 kg)(2.5 m)2 =
2500 kgm2
But this is just the Merry-go-round, we need the total moment of
inertia. Treating the children as point 25 kg masses at the edge (r =
2.5 m) their moment of inertia would be each:
I =
mr2 = (25 kg)(2.5 m)2 = 156.25 kgm2
The total moment of inertia is
I =
2500 kgm2 + 156.25 kgm2 + 156.25 kgm2 = 2812.5 kgm2
Now apply:
w =
wo + at :
wo
= 0;
w
= 2.0944 rad/s;
t = 10.0 s
a
= 0.20943951 rad/s/s
And finally the angular equivalent of F = ma:
t =
Ia
t
= (2812.5 kgm2)(0.20943951
rad/s/s) = 589 Nm of torque
Since force is applied at a 90o
angle to the radius, the torque is:
t = rF
So F =
t/r
= (589.05 Nm)/(2.5 m) = 236 N = 240 N
(Table of contents)
46. A helicopter rotor blade can be considered a long
thin rod, as shown in Fig. 8-42. If each of the three rotor helicopter blades is
3.75m long and has a mass of 160kg, calculate the moment of inertia of the three
rotor blades about the axis of rotation. How much torque must the motor apply to
bring the blades up to a speed of 5.0rev/s in 8.0s?
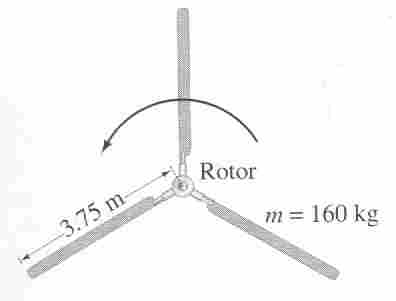
The moments of inertia are listed on p. 223, and a long thin rod through its
end is:
I =
1/3ML2
so each rotor has a moment of inertia of:
I =
1/3(160 kg)(3.75 m)2 =
2500 kgm2 = 750 kgm2
Three rotors would have three times this moment:
I = (750 kgm2)3 = 2250 kgm2
Now we need to solve a cute kinematics question:
wo
= 0
w
= (5 Revolutions/s)(2p
radians/revolution) = 31.416 rad/s
t = 8.0 s
Now apply:
w =
wo + at
a
= 3.927 rad/s/s
And now find the torque using F = ma:
t =
Ia
t
= (2250 kgm2)(3.927
rad/s/s) = 8836 Nm = 8800 Nm of torque
(Table of contents)
48. An Atwood's machine consists of two masses, m1 and
m2, which are connected by a massless inelastic cord that passes over a pulley,
Fig.8-44. If the pulley has radius R and moment of inertia I about its
axle, determine the acceleration of the masses m1 and m2, and compare to the
situation in which the moment of inertia of the pulley is ignored. [Hint: The
tensions Ft1 and Ft2 are not necessarily equal.]
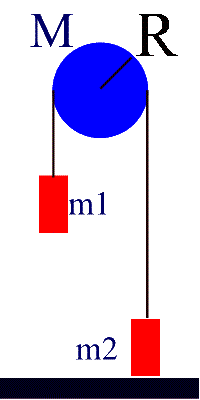
Let T1 = the tension in the cord above m1, and
T2 = the tension in the cord above m2
I = the pulley moment of inertia
R = pulley radius
The hint they give is valid, if you consider the system in acceleration, (I
will assume that the m1 accelerates downwards) then T1
must be bigger than T2 as it is this difference that causes the
pulley to accelerate.
Let's start with the pulley. It has two torques, a clockwise torque due
to T2:
t = rF =
RT2
And a ACW (Anti Clockwise) torque die to T1:
t = rF =
RT1
Making ACW positive (That is, I am guessing that this is the direction the
system will go) the net torque is:
tnet
=
RT1- RT2
Which is equal to
Ia
tnet
=
Ia = RT1- RT2
But be want to make everything linear, so substitute:
a
= a/r:
Ia
= rT1- rT2
I(a/R)
= rT1- rT2
Divide both sides by R
Ia/R2
= T1- T2
And now there are two other objects to set up F = ma equations for:
Mass 1:
<m1g - T1> = m1a
Mass 2:
<T2 - m2g> = m2a
So now we have three unknowns, T1, T2 and a, and these
three equations:
1/2Ma
= T1- T2
<m1g - T1> = m1a
<T2 - m2g> = m2a
Should be solvable, and the obvious recipe is to solve the last two for T1
and T2, and plug these into the first:
<m1g - T1> = m1a
T1 = m1g - m1a
<T2 - m2g> = m2a
T2 = m2a + m2g
Finally, put these into
Ia/R2
= T1- T2
Ia/R2
= (m1g - m1a)- (m2a
+ m2g) = m1g - m1a- m2a
- m2g
Good golly, I guess we're solving for a, so let's get all terms with
acceleration in it on the left side:
Ia/R2
+ m1a + m2a =
m1g - m2g = g(m1 - m2)
Factor out the a:
a(I/R2
+ m1 + m2) =
g(m1 - m2)
a = g(m1 - m2)/(I/R2
+ m1 + m2)
Without the moment of inertia of the pulley it is just the two mass equations
we have to solve:
<T - m2g> = m2a
<m1g - T> = m1a
If the pulley has no moment of inertia, then T1 and T2
are the same
adding the two equations together:
<T - m2g> = m2a
<m1g - T> = m1a
m1g - m2g = m2a + m1a = a(m2
+ m1)
a = (m1 - m2)g/(m2 + m1)
Which is exactly what we got in the previous part, but without the inertial
term of the pulley of I/R2.
(Table of contents)
53. A merry-go-round has a mass of 1640kg and a radius
of 8.20m. How much net work is required to accelerate it from rest to a rotation
rate of one revolution in 8.00s? (Assume it is a solid cylinder).
w
= Dq/Dt
= (1 Revolution)(2p
radians/revolution)/(8.00 s) = 0.7854 rad/s
The moments of inertia are listed on p. 223, and a cylinder through the center
is:
I = 1/2mr2
so the merry-go-round has a moment of inertia of:
I =
1/2(1640 kg)(8.20 m)2 =
2500 kgm2 = 55136.8 kgm2
The energy required would be the kinetic energy it has when
you are done:
Ek rot = 1/2Iw2
Ek rot = 1/2(55136.8
kgm2)(0.7854 rad/s)2 =
17006 J = 1.70 x104 J
(Table of contents)
54. (a) Calculate the translational and rotational speed
of sphere (radius 20.0cm and mass 1.20kg), that rolls without slipping down a
30.00 incline that is 10.0m long, when it reaches the bottom. Assume
it started from rest. (b) What is its ratio of translational to rotational KE at
the bottom? Try to avoid putting in numbers until the end so you can answer: (c)
do your answer in (a) and (b) depend on the radius of the sphere or its mass?
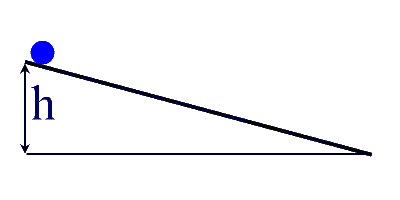
Let's use energy for this guy, but first we must calculate the height,
which would be opp = hyp(sinq),
so the height is h = (10.0 m)sin(30o) = 5.00 m
Assuming the sphere starts at rest, it has only potential energy at
the top of the plane, and at the bottom, as it is rolling, it has both
translational and rotational kinetic energy. So our energy equation
looks like:
mgh =
= 1/2mv2
+
1/2Iw2
I am going to substitute to get rid of angular quantities.
I = 2/5mr2 for a sphere, and w
= v/r:
mgh = 1/2mv2
+
1/2(2/5mr2)(v/r)2
mgh = 1/2mv2
+
1/2(2/5mr2)(v2/r2)
cancel the r2
mgh = 1/2mv2
+
1/2(2/5m)(v2)
mgh = 1/2mv2
+
(2/10m)(v2)
= 7/10mv2
mgh = 7/10mv2
finally cancel the m
gh = 7/10v2
so the final velocity is
v = Ö(10gh/7)
= Ö(10(9.80
m/s/s)(5.00 m)/7)
= 8.367 m/s
Now we can find the angular velocity of the marble:
w
= v/r = (8.367 m/s)/(.20 m) = 41.83 rad/s
The rotational kinetic energy can be found from the linear velocity if we
follow the substitutions:
Ekrot =
1/2Iw2
= 1/2(2/5mr2)(v/r)2
= (2/10m)(v2)
Now let's find the translational kinetic energy:
KE = 1/2mv2
The ratio of these is
Ratio = {1/2mv2
}/{(2/10m)(v2)}=
{1/2
}/{2/10}= 2.5 - and no, it does not depend on the
radius or mass of the sphere.
Table of contents)
55. Two masses, m1 = 18.0kg and m2=26.5kg, are
connected by a rope that hangs over a pulley (as in Fig.8-44). The pulley is a
uniform cylinder of radius 0.26m and mass 7.50kg. Initially, m1 is on the
ground, and m2 rests 3.00m above the ground. If the system is now released, use
conservation of energy to determine the speed of m2 just before it strikes the
ground. Assume the pulley is frictionless.
|
Before |
After |
|
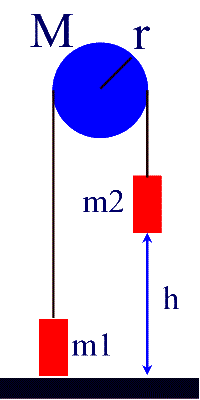
|
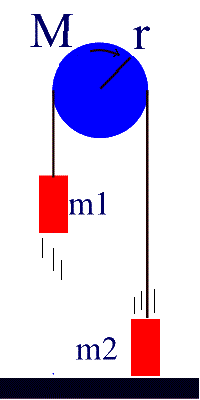
|
Energy time. The potential energy of mass 1 goes to
the translational kinetic energies of both masses and to the rotational
kinetic energy of the pulley as well as the potential energy of mass 2, just
before mass 1 strikes the ground:
m2gh
= 1/2m1v2
+1/2m2v2
+ m1gh + 1/2Iw2
Substitute for the rotational term:
w
= v/r
I = 1/2mr2
m2gh = 1/2m1v2
+1/2m2v2
+ m1gh + 1/2(1/2Mr2)(v/r)2
m2gh = 1/2m1v2
+1/2m2v2
+ m1gh + 1/4Mv2
Now solve for the final velocity:
m2gh -m1gh = 1/2m1v2
+1/2m2v2
+ 1/4Mv2
m2gh -m1gh = v2( 1/2m1
+1/2m2 + 1/4M)
gh(m2 -m1) = v2( 1/2m1
+1/2m2 + 1/4M)
gh(m2 -m1)/( 1/2m1
+1/2m2 + 1/4M)
= v2
v = Ö{gh(m2
-m1)/( 1/2m1
+1/2m2 + 1/4M)}
v = Ö{(9.80
m/s/s)(3.00 m)(25.6 kg -18.0 kg)/( 1/2(25.6
kg) +1/2(18.0 kg) + 1/4(7.50
kg))}
v = 3.072 m/s - which is correct, and the book gets 3.22, which is wrong I
think
(Table of contents)
59. A diver (such as the one shown in Fig. 8-28) can
reduce her moment of inertia by a factor of about 3.5 when changing from the
straight position to the tuck position. If she makes two rotations in 1.5s when
in the tuck position, what is her angular speed (rev/s) when in the straight
position?
This is a conservation of angular momentum problem.
The angular kinetic energy would not be conserved as the diver would do
work in tucking that would be manifested as rotational kinetic
energy. (it would go up)
Now, the formula for angular momentum is:
L = Iw
So basically, L before = L after:
I1w1
= I2w2
Let I1 be the moment of inertia when she is straight, and I2
be the moment in the tucked position:
I1 = (3.5)I2
w1
= (2 rev)/(1.5 s) = 1.3333 rev/s
(3.5)I2w1 =
I2(1.3333 rev/s)
(3.5)w1 =
(1.3333 rev/s)
w1 =
(1.3333 rev/s)/(3.5) = 0.38 rev/s
(Table of contents)
60. A figure skater during her final can increase her
rotation rate from an initial rate of 1.0 rev every 2.0s to a final rate of
3.0rev/s. If her initial moment of inertia was 4.6kg.m2 , what is her
final moment of inertia? How does she physically accomplish this change?
This is a conservation of angular momentum problem.
Now, the formula for angular momentum is:
L = Iw
So basically, L before = L after:
I1w1
= I2w2
w1
= (1 rev)/(2 s) = .5 rev/s
w2
= 3.0 rev/s
I1
= 4.6 kgm2
(4.6 kgm2)(.5 rev/s) = I2(3.0
rev/s)
I2
= 0.77 kgm2 (Note that the units cancel, so we don't have to convert to radians per second)
Skaters can change their moment of inertia by pulling in their arms and legs
closer tot he axis of rotation
(Table of contents)
65. A uniform disk, such as a record turntable, turn at
7.0rev/s around a frictionless spindle. A non-rotating rod, of the same mass as
the disk and length equal to the disk's diameter, is dropped onto the freely spinning
disk. They then both turn around the spindle with their centers superposed, Fig.
8-46. What is the angular velocity in rev/s of the combination?
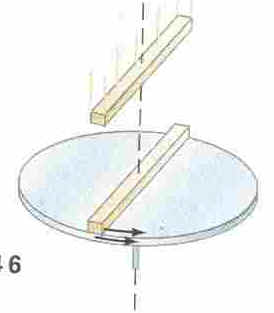
The formula for angular momentum is:
L = Iw
Conservation of angular momentum says that L before = L after:
I1w1
= I2w2
The moments of inertia are listed on p. 223 in your text, a disk or cylinder
through the center is:
I = 1/2mr2
And a thin rod through the center is
I = 1/12ml2
and the rod is 2r long, so the moment of inertia in terms of r is:
I = 1/12m(2r)2
I = 4/12mr2 = 1/3mr2
So the moment of inertia before the rod is dropped on is just the disk:
I1 = 1/2mr2
And after it the rod is dropped on, it is both moments:
I2 = 1/2mr2 + 1/3mr2
= 5/6mr2
So plug these into:
I1w1
= I2w2
(1/2mr2)(7.0
rev/s) = (5/6mr2)w2
(1/2)(7.0 rev/s) = (5/6)w2
w2
= 4.2 rev/s
(Table of contents)
66. A person of a mass 75kg stands at the center of a
rotating merry-go-round platform of radius 3.0m and moment of inertia 1000kg.m2
. The platform rotates without friction with angular velocity 2.0rad/s. The
person walks radially to the edge of the platform. (a) Calculate the angular
velocity when the person reaches to the edge. (b) Compare the rotational kinetic
energies of the system of platform plus person before and after the person's
walk.
This is a conservation of angular momentum problem.
Now, the formula for angular momentum is:
L = Iw
So basically, L before = L after:
I1w1
= I2w2
The trick to solving these is to figure out what the change in moment of
inertia is, and then apply the concept of conservation of angular momentum to
it.
With a person on a merry-go-round, the moment of inertia would be the moment
of inertia of the person plus the moment of inertia of the merry-go-round.
In this case the person starts at the center of the rotating merry-go-round,
and so I think we are to say their moment of inertia is zero or negligible (it
would be small), but then they move to the outside edge of the merry-go-round,
and in the after picture, have a significant moment of inertia. The
moment of inertia of the merry-go-round is the same before and after and given
as 1000 kgm2
So the total moment of inertia before is just that of the merry-go-round
itself:
I1 = 1000 kgm2
When the person walks to the edge, they have a moment of inertia due to a
point mass
I = mr2 = (75 m)(3.0 m)2 = 675 kgm2
So the total moment of inertia after they walk to the edge is:
I2 = 1000 kgm2 + 675 kgm2 = 1675 kgm2
Now we are ready to apply conservation of angular momentum:
I1w1
= I2w2
(1000 kgm2)(2.0 rad/s) = (1675 kgm2)w2
w2
= 1.194 rad/s
Now let's calculate the rotational kinetic energy before and after:
Before:
Ek rot = 1/2I1w12
Ek rot = 1/2(1000
kgm2)(2.0 rad/s)2
= 2000 J
After:
Ek rot = 1/2I2w22
Ek rot = 1/2(1675
kgm2)(1.194
rad/s)2
= 1194. J
The final kinetic energy is (1194. J)/(2000 J) = 60. % of the original, a
decrease of 40.%
We would not expect the kinetic energy to remain constant. It does not,
because the system does work on the person as they move toward the
outside. (As they move out, they have to exert a retarding force to keep
from speeding up - there is a "centrifugal" force trying to make
them go to the outside, so the effect is the same as moving a box from a high
shelf to a low shelf, you exert an upward force, but the displacement is
downward, so the work is negative)
(Table of contents)
69. Suppose our Sun eventually collapses in a white
dwarf, in the process losing about half its mass and winding up with a radius
1.0 percent of its existing radius. Assuming the loss mass carries away no
angular momentum, what would the sun's new rotation rate be? (Take the Sun's
current period to be about 30 days.) What would be its final KE in term of its
initial KE of today?
This is a conservation of angular momentum problem.
Now, the formula for angular momentum is:
L = Iw
So L before = L after:
I1w1
= I2w2
The trick to solving these is to figure out what the change in moment of
inertia is, and then apply the concept of conservation of angular momentum to
it.
The sun and the white dwarf will both be spherical, (one might argue with the
idea that they are homogeneous, as the density of the edge of the sun is not
nearly what it is in the center...but, let's not worry about this...)
A uniform sphere (p. 223) is 2/5mr2:
I1 = 2/5mr2 = 2/5MR2
Where M and R are the current mass and radius
And
w1
=1 rev/30 days
After, the sun has half the mass, and 1/100 the radius:
I2 = 2/5(M/2)(R/100)2
= (2/5MR2)/(20,000)
Plugging into conservation of angular momentum:
I1w1
= I2w2
( 2/5MR2)(1 rev/30 days) = (2/5MR2)/(20,000)w2
(1 rev/30 days) = w2/(20,000)
w2
= (20,000)(1 rev/30 days)
w2
= (20,000)(1 rev/30 days)(2p
radians/revolution)(1day/24.3600 sec)
= 0.048481368 rad/sec = .048 rad/sec
As for the ratio of kinetic energies,
Before:
Ek rot = 1/2Iowo2
=
1/2(2/5MR2)(1 rev/30 days)2
After:
Ek rot = 1/2Iowo2
=
1/2(2/5(M/2)(R/100)2)((20,000)(1 rev/30
days))2
Ek rot = 1/2Iowo2
= (20,000)2/(20,000){
1/2(2/5MR2)(1 rev/30 days)2}
Which is just 20,000 times what it was before
(Table of contents)
80. A uniform rod of mass M and length L can pivot
freely (i.e., we ignore friction) about a hinge attached to a wall, as in Fig.
8-50. The rod is held horizontally and then released. At this moment of release,
determine (a) the angular acceleration of the rod and (b) the linear
acceleration of the tip of the rod. Assume that the force of gravity acts at the
center of the mass of the rod, as shown. [Hint: See Fig. 8-20g.]
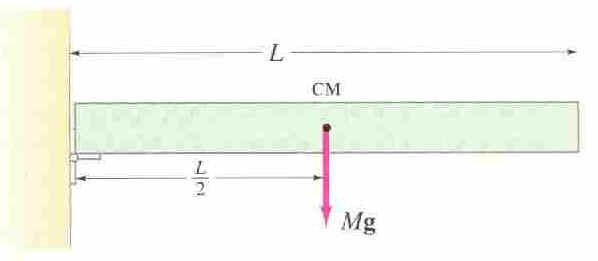
To find the angular acceleration of the system, ultimately we are going to
use the angular equivalent of F = ma:
t =
Ia
We just have to figure out the torque, and the moment of inertia.
For the moment of inertia, let's use a thin rod rotating about its end:
I = 1/3ML2
For the torque, lets assume that the entire weight Mg acts at a point midway
from the hinged end L/2:
t = rF
= (L/2)(Mg) = LMg/2
Now we are ready to use
t =
Ia
LMg/2
= (1/3ML2)a
3LMg
= 2ML2a
3Mg
= 2MLa
3g
= 2La
a
= 3g/2L
The tangential acceleration is
a = ar
Since the radius at the very end is L
a = ar
= (3g/2L)L = 3g/2 which is greater than the acceleration
of gravity. This is why it would pull away from an object that was just
placed on it at the tip
(Table of contents)




