Problem Set 8.8: | 1
| 3 |
6 | 7 | 8 | 9 |
10
| 16 | 20 | 21 |
22 | 29 | 31
| 34 | 39 | 43 | 50
| 51 | 53 | Go up
- by Sonja Scherer, To Chong, and Chris Murray, 2002
1. What are the following angles expressed in radians:
(a) 30º, (b) 57º, (c) 90º, (d) 360º and (e) 420º?
Since there are 2p
radians and 360o in a circle, you can use a simple proportion to do
unit conversions:
n/360o = radians/2p
so
30o/360o = radians/2p
radians = 0.524
You are smart enough to do the rest......: - )
(Table of contents)
3.
Eclipses happen on Earth because of an amazing coincidence. Calculate, using the
information inside the front cover, the angular diameter (in radians) of the Sun
and the angular diameter of the Moon, as seen on Earth.
The angle in radians is equal to the arc length, divided by
the radius. The arc length would be the diameter
of the sun or the moon, and the radius would be their distance from us:
Moon:
radius = 1.74x103km, diameter = 3.48x103km
distance from us = 384x103km
Subtended angle:
q
= s/r = (3.48x103km)/(384x103km)
= 0.0090625
Sun:
radius = 6.96x105km, diameter = 1.392x106km
distance from us = 149.6x106km
q
= s/r = (1.392x106km)/(149.6x106km)
= 0.009304813
so 0.0090625 is almost equal to 0.009304813
(Table of contents)
6. A 0.35-m diameter grinding wheel rotates at 1800 rpm.
Calculate its angular velocity in rad/s.
(1800 Revolutions/Minute)(2p
radians/revolution)(1 minute/60 sec) = 188.5 rad/s
(Table of contents)
7. What is the linear speed and acceleration of a point
on the edge of a grinding wheel in Problem 6?
Since they give us the diameter, the radius = (0.35 m/2)
The linear speed of a point on the edge of grinding wheel is:
v = rw
= (0.35 m/2)(188.5 rad/s) = 33m/s
The acceleration of a that point is:
a= rw2
= (0.35 m/2)(188.5 rad/s)2 = 62188.14m/s2
(Table of contents)
8. A 33-rpm phonograph record reaches its rated
speed 1.8 s after it is turned on. What was the angular acceleration?
wo
= 0
w
= (33 Revolutions/Minute)(2p
radians/revolution)(1 minute/60 sec) = 3.456 rad/s
t = 1.8 s
The angular acceleration is:
a = Dw/Dt
= (3.456
rad/s)/(1.8
s) = 1.92 rad/s2
(Table of contents)
9. Calculate the angular velocity of (a) the second hand,
(b) the minute hand, (c) the hour hand, of a clock. State in rad/s. (d) What is
the angular acceleration in each case?
(a) The angular velocity of the second hand is:
w =
Dq/Dt
= 2p/(60
sec)
= 2p/60
= 0.10472rad/s
(b)
The angular velocity of the minute hand: w =
Dq/Dt
= 2p/(3600
sec) =
2p/3600
= 0.001745rad/s
(c)
The angular velocity of the hour hand is: w =
Dq/Dt
= 2p/(12*3600
sec) =
2p/43200
= 0.000145444rad/s
(d)
Since the angular velocity is constant for all cases, thus the angular
acceleration is zero.
a = Dw/Dt
= (w2- w1)/Dt
(w1 = w2)
(Table of contents)
10. The blades in an blender rotate at a rate of 7500
rpm. When the motor is turned off during an operation, the blades slow to rest
in 3.0 s. What is the angular acceleration as the blades slow down?
The angular acceleration is:
a = Dw/Dt
= (w2- w1)/Dt
= (0 - 2pf)/Dt
= -2p*7500rpm/60s/minute/3s
= -261.8rad/s
(Table of contents)
16. How fast (in rpm) must a centrifuge rotate if a
particle 7.0 cm from the axis of rotation is to experience an acceleration of
100,000 g's?
100,000 'g's = (100,000)(9.8 m/s/s) = 980,000 m/s/s
Centripetal acceleration in terms of angular velocity and radius is:
a= rw2
so
w
= Ö(a/r)
= Ö{(980,000
m/s/s)/(.070 m)}
= 3742 rad/s
And now convert to RPMs:
(3742 rad/s)(revolution/2p
radians)(60 sec/1 minute) = 35730 RPMs = 36,000 RPMs
(Table of contents)
20. A phonograph turntable reaches its speed of 33 rpm
after making 1.7 revolutions. What was its angular acceleration?
w
= (33 Revolutions/Minute)(2p
radians/revolution)(1 minute/60 sec) = 3.456 rad/s
q
= (1.7 rev)(2p
radians/revolution) = 10.68 radians
Now we can find the angular acceleration:
w2 = wo2
+ 2aq
: wo
= 0; q = 10.68 radians;w
= 3.456 rad/s
a
= 0.56 rad/s/s
(Table of contents)
21. A centrifuge accelerates from rest to 15,000 rpm to
220 s. Through how many revolutions did it turn in this time?
w
= (15,000 Revolutions/Minute)(2p
radians/revolution)(1 minute/60 sec) = 1570.8 rad/s
t = 220 s
wo
= 0
Now the formula I want to use is only in the formula packet in its linear
form, but it works just as well in angular form
s = (u+v)t/2
Which is
q
= (wo+w)t/2
Now let's plug in numbers:
q
= (0+1570.8 rad/s)(220 s)/2 = 172787.5959 radians
But the problem wanted revolutions, so let's change the units:
q
= (172787.5959 radians)(revolution/2p
radians) = 27500 revolutions
(Table of contents)
22. An automobile engine slows down from 4000 rpm to
1200 rpm in 3.5 s. Calculate (a) its angular acceleration, assumed uniform, and
(b) the total number of revolutions the engine makes in this time.
wo
= (4000 Revolutions/Minute)(2p
radians/revolution)(1 minute/60 sec) = 418.9 rad/s
w
= (1200 Revolutions/Minute)(2p
radians/revolution)(1 minute/60 sec) = 125.7 rad/s
t = 3.5 s
Let's find the acceleration first:
w = wo + at
: wo
= 418.9 rad/s; w
= 125.7 rad/s; t = 3.5 s
a
= -83.8 rad/s/s
And the displacement (Angular)
Now the formula I want to use is only in the formula packet in its linear
form, but it works just as well in angular form
s = (u+v)t/2
Which is
q
= (wo+w)t/2
Now let's plug in numbers:
q
= (125.7 rad/s+418.9 rad/s)(3.5 s)/2 = 952.9 radians
But the problem wanted revolutions, so let's change the units:
q
= (952.9 radians)(revolution/2p
radians) = 151.7 revolutions
(Table of contents)
29. What is the maximum torque exerted by a 55-kg person
riding a bike if the rider puts all her weight on each pedal when climbing a
hill? The pedals rotate in a circle of radius 17 cm.
The formula for torque is:
t = r
x F = rFsinq
The word "maximum" implies that the force is applied at a 90o
angle to the radius, so the factor sinq
becomes 1, and really the torque is:
t = rF
The force is the weight of the cyclist:
F = ma
F = (55 kg)(9.8 N/kg) = 539 N
So
t = rF
= (.17 m)(539 N) = 92 Nm
(Table of contents)
31. Calculate the net torque about the axle of the wheel
shown below. Assume that a friction torque of 0.40 m N opposes the motion.
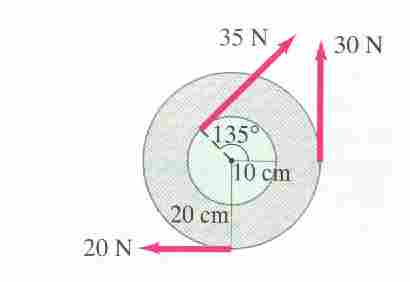
Here we are simply going to add the torques, making CW
torques positive, and ACW (Anti Clockwise - it's an IB term) torques
negative. All angels are 90o so it makes it pretty
easy: (The 135o angle indicated is not relevant:)
t35 = rF
= (.10 m)(35 N) = +3.5 Nm CW
t30 =
-rF = -(.20 m)(30 N) = -6.0 Nm (ACW)
t20 =
rF = (.20 m)(20 N) = +4 Nm CW
Adding all these together:
t =
+1.5 Nm CW
But there is a .4 Nm torque opposing the motion, so assuming that the object
is rotating CW, then the .40 Nm torque would be acting ACW, and the net torque
would be:
t =
+1.5 Nm - .40 Nm = 1.1 Nm CW
(Table of contents)
34. Calculate the moment of inertia of a 12.2-kg sphere
of radius 0.623 m when the axis of rotation is through its center.
The moments of inertia are listed on p. 223, and a uniform
sphere through its center is:
I =
2/5mr2
so
I =
2/5(12.2)(.623)2 = 1.89
kgm2
(Table of contents)
39. In order to get a flat uniform cylindrical satellite
spinning at the correct rate, engineers fire four tangential rockets as shown
below. If the satellite has a mass of 2600 kg and a radius of 3.0 m, what is the
required steady force of each rocket if the satellite is to reach 30 rpm in 5.0
min?
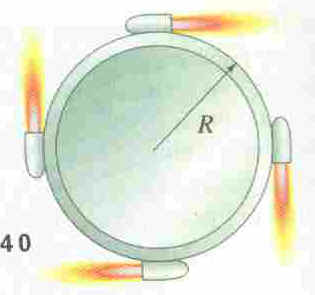
The moments of inertia are listed on p. 223, and a uniform
cylinder through its center is:
I =
1/2mr2
so
I =
1/2(2600 kg)(3.0)2 =
11700 kgm2
This leaves an obvious kinematics problem to solve (we need the angular
acceleration)
wo
= 0
w
= (30 Revolutions/Minute)(2p
radians/revolution)(1 minute/60 sec) = 3.14159 rad/s
t = (5.0 min)(60 sec/min) = 300 sec
Let's find the acceleration first:
w = wo + at
: wo
= 0; w
= 3.14159 rad/s; t = 300 s
a
= 0.010472 rad/s/s
So now we can use the angular version of F = ma:
t =
Ia= (11700 kgm2)(0.010472 rad/s/s) = 122.5 Nm
The formula for torque is:
t = r
x F = rFsinq
The force is applied at a 90o angle to the radius, so the the
factor sinq
becomes 1, and really the torque is:
t = rF
So we can now solve for the net tangential force at the edge of the satellite
(at radius of 3.0 m)
t = rF
122.5 Nm
= (3.0
m)F
F = 40.84 N, but since there are four engines working together, each one needs
to exert one fourth of this:
F/4 = (40.84 N)/4 = 10.2 N
(Table of contents)
43. A centrifuge rotor rotating at 10,000 rpm is shut
off and is eventually brought to rest by a frictional force of 1.20m N. If the
mass of the rotor is 4.80 kg and it can be approximated as a solid cylinder of
radius 0.0710m, through how many revolutions will the rotor turn before coming
to rest, and how long will it take?
The moments of inertia are listed on p. 223, and a uniform
cylinder through its center is:
I =
1/2mr2
so
I =
1/2(4.80 kg)(.0710 m)2
= 0.0120984 kgm2
Since there is a frictional torque of 1.20 Nm, we can use the angular
equivalent of F = ma to find the angular deceleration:
t =
Ia
-1.20 Nm = (0.0120984 kgm2)a
a
= -99.19 rad/s/s
Now we have a kinematics question to solve:
wo
= (10,000 Revolutions/Minute)(2p
radians/revolution)(1 minute/60 sec) = 1047.2 rad/s
w
= 0
a
= -99.19 rad/s/s
Let's find the time first:
w = wo + at
: wo
= 1047.2 rad/s; w
= 0 rad/s; a
= -99.19 rad/s/s
t = 10.558 s = 10.6 s
And the displacement (Angular)
Now the formula I want to use is only in the formula packet in its linear
form, but it works just as well in angular form
s = (u+v)t/2
Which is
q
= (wo+w)t/2
: wo
= 1047.2 rad/s; w
= 0 rad/s; t = 10.558 s
q
= (125.7 rad/s+418.9 rad/s)(3.5 s)/2 = 952.9 radians
But the problem wanted revolutions, so let's change the units:
q
= (5528.075087 radians)(revolution/2p
radians) = 880. revolutions
(Table of contents)
50. A bowling ball of mass 7.3 kg and radius 9.0 cm
rolls without slipping down a lane at 4.3 m/s. Calculate its total kinetic
energy.
The moments of inertia are listed on p. 223, and a uniform
sphere through its center is:
I =
2/5mr2
so
I =
2/5(7.3 kg)(.090 m)2 =
0.023652 kgm2
The angular velocity can be had from the tangential relationship between
angular and tangential velocity:
w
= v/r = (4.3 m/s)/(.090 m) = 47.778 rad/s
And finally, the total kinetic energy is the sum of its translational (1/2mv2)
and rotational (1/2Iw2)
kinetic energies:
Ektotal = 1/2mv2
+ 1/2Iw2
Ektotal = 1/2(7.3 kg)(4.3)2
+ 1/2(0.023652 kgm2)(47.778
rad/s)2
Ektotal = 67.4885 J + 26.9954 J = 94 J
An interesting thing happens if we make substitutions instead:
Ektotal = 1/2mv2
+ 1/2Iw2
I = 2/5mr2
w
= v/r
Substituting:
Ektotal = 1/2mv2
+ 1/2(2/5mr2)(v/r)2
Ektotal = 1/2mv2
+ 2/10(mr2)(v2/r2)
Now the r2 factors cancel
Ektotal = 1/2mv2
+ 2/10mv2
Ektotal = 7/10mv2
An answer totally independent of the radius of the ball!!!
(Table of contents)
51. A centrifuge rotor has a moment of inertia of
3.15 x 10^-2 kg m^2. How much energy is required to bring it from rest to 8000
rpm?
The energy required would be the kinetic energy it has when
you are done:
w
= (8000 Revolutions/Minute)(2p
radians/revolution)(1 minute/60 sec) = 837.76 rad/s
I = 3.15x10-2 kgm2
Ek rot = 1/2Iw2
Ek rot = 1/2(3.15x10-2
kgm2)(837.76 rad/s)2 =
11054 J
(Table of contents)
53. A merry-go-round has a mass of 1640 kg and a radius
of 8.20 m. How much net work is required to accelerate it from rest to a
rotation rate of one revolution in 8.00 s? (Assume it is a solid cylinder.)
The moments of inertia are listed on p. 223, and a uniform
cylinder through its center is:
I =
1/2mr2
so
I =
1/2(1640 kg)(8.20)2 =
55136.8 kgm2
We can find the final angular velocity:
w = Dq/Dt
= (1 rev)/(8.00 s)(2p
radians/rev) = 0.785398163 rad/s
The work will be the rotational kinetic energy
Ek rot = 1/2Iw2
Ek rot = 1/2(55136.8
kgm2)(0.785398163 rad/s)2 =
17000 J
(Table of contents)