Problem Set 7.3: | 1
| 2 |
3 | 4 | 5 | 6
|
7 | 8 | 9 | 10
| 11 | 14
| 15 | 16 | 18
| Go up
- by Chris Murray, Sonja Scherer, To Chong 2002
1. What is the magnitude of the momentum of a 22-g
sparrow flying with a speed of 8.1 m/s?
m = 22 g = .022 kg
p = mv = (.022 kg)(8.1 m/s) = .1782 kgm/s = .18 kgm/s
(Table of contents)
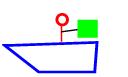
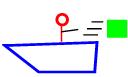
2. A child in a boat throws a 5.40-kg package out
horizontally with a speed of 10.0m/s, See below. Calculate the velocity of the
boat immediately after, assuming it was initially at rest. The mass of the child
is 26.0 kg and that of the boat is 55.0 kg.
Here you are comparing the momentum of the boat, boy and box when they are
at rest (no momentum) to just after he throws the package. In the after
picture, you have the 55.0 kg boat and the 26.0 kg boy moving (to the left) at
some unknown velocity, and the package moving to the right (+) at 10.0 m/s
 |
 |
| (Momentum is
Zero) 0
= |
(26.0 kg + 55.0 kg)v + (5.40 kg)(+10.0 m/s) |
v = -.667 m/s
(Table of contents)
3. Calculate the force exerted on a rocket, given that
the propelling gases are expelled at a rate of 1300kg/s with a speed of 40,000
m/s (at the moment of takeoff).
We know that
Impulse = Dp = FDt
and implicitly, Dp = mDv
so ultimately,
FDt = mDv
Good so far, but what do we put into the equation? We know that in 1
second, 1300 kg of combustion products leaves the engine undergoing a change
in velocity of 40,000 m/s.
FDt = mDv
F(1 s) = (1300 kg)(40,000 m/s)
F = 52000000 N = 52 MN (M = Mega = 106)
(Table of contents)
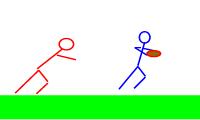
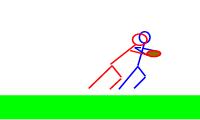
4. A halfback on an apparent breakaway for a touchdown is
tacked from behind. If the halfback has a mass of 95 kg and was moving 4.2 m/s
when he was tackled by an 85-kg cornerback running at 5.5 m/s in the same
direction, what was their mutual speed immediately after the touchdown-saving
tackle?
You have in the first frame, the pursuing 85 kg cornerback running to the
right (+) at 5.5 m/s, overtaking the 95 kg halfback moving at 4.1 m/s to the
right (+) as well.. In the second frame, you have the two of them
together 85 kg + 95 kg = 180 kg moving (to the right) at some unknown
velocity. I am going to make to the right positive.
 |
 |
| (85 kg)(5.5 m/s) + (95 kg)(4.1 m/s) = |
(180 kg)v |
v = 4.761 m/s = 4.8 m/s
(Table of contents)
5. A 12,500-kg railroad car travels alone on a level
frictionless track with a constant speed of 18.0m/s. A 5750-kg additional load
is dropped on a car. What then will be the car's speed?
Assuming the load is not moving when it is dropped in the
rail car, we compare the momentum before to the momentum after:
mv = mv
(12,500 kg)(18.0 m/s) = (12,500 kg + 5750 kg)v
v = 12.329 = 12.3 m/s
(Table of contents)
6. A 9500-kg boxcar traveling at 16 m/s strikes a second
car. The two stick together and move off with a speed of 6.0 m/s. What is the
mass of the second car?
You have in the first frame, the 9500 kg boxcar moving to the right (+) at
16 m/s, and the second boxcar sitting still (assumed) on the tracks. In
the second frame, the two boxcars with a total mass of 9500 kg + M, where M is
the unknown mass of the second car, move along to the right (+) at 6.0
m/s. I am going to make to the right positive.
 |
 |
| (9500 kg)(16 m/s) + 0 = |
(9500 kg + M)(6.0 m/s) |
M = 15833.33 kg = 1.6x104 kg
(Table of contents)
7. A gun is fired vertically into a 1.40-kg block of wood
at rest directly above it. If the bullet has a mass of 21.0 g and a speed of
210m/s, how high will the block rise into the air after the bullet becomes
embedded in it?
This is a two-parter, in the first part, where the bullet
collides with the block, I will use conservation of momentum. Energy
would not be conserved as it is not an elastic collision. In the second
part, where the block starts from its original height with some velocity, and
goes up to some height, I will use conservation of energy. I could also
use simple linear kinematics, but I think the book wants me to use energy.
Part I - the bullet strikes the block. In the first frame you have the
.021 kg bullet moving upward (+) at 210 m/s, and the block at rest. In
the second frame you see the bullet block combo (1.40 kg + .021 kg = 1.421 kg)
moving up at a velocity that we need to know:
 |
 |
| (.021 kg)(210 m/s) +
0 = |
(1.40 kg + .021 kg)v |
v = 3.103 m/s
Part II - the bullet-block combo starts at zero elevation,
and rises some unknown height into the air. Kinetic energy turns into
potential energy:
 |
 |
| 1/2mv2
= |
mgDh |
1/2mv2 = mgDh
m will cancel:
1/2v2
= gDh
Dh = v2/2g
Dh = (3.103 m/s)2/2(9.8 N/kg) = 0.491 m
(Table of contents)
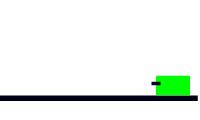
8. A 15-g bullet strikes and becomes embedded in a
1.10-kg block of wood placed on a horizontal surface just in front of the gun.
If the coefficient of kinetic friction between the block and the surface is
0.25, and the impact drives the block a distance of 9.5 m and before it comes to
rest, what was the muzzle speed of the bullet?
This is also a two-parter, in the first part, where the bullet
collides with the block, I will use conservation of momentum. Energy
would not be conserved as it is not an elastic collision. In the second
part where the block starts out with a kinetic energy and then comes to a
halt, having done work against friction, I will use conservation of energy. I could also
use simple linear kinematics, but I think the book wants me to use energy.
Here is a cartoon of the whole thing:
Let's start with the last part, where the kinetic energy turns into work
against friction:
 |
 |
| 1/2mv2
= |
Fs |
1/2mv2 = Fs
Since F = the force of friction, F = Ffr = µkFN
and FN
= mg in this case, so ultimately, F = µkmg
So let's substitute this in for F:
1/2mv2 = Fs
1/2mv2 = µkmgs
And so m cancels, and we solve for the velocity:
1/2v2 = µkgs
v2 = 2µkgs
v = Ö{2µkgs}
= Ö{2(.25)(9.80
N/kg)(9.5 m)} = 6.823 m/s
Now we need to do some momentum:
In the first frame, you have the 15 g (.015 kg) bullet moving
to the right at an unknown velocity, and the block of wood at rest. In
the second frame, you have the bullet block combo moving to the right at 6.823
m/s as we figured out in the first part above.
 |
 |
| (.015 kg)v +
0 = |
(1.10 kg + .015 kg)(6.823 m/s) |
v = 507.16 m/s = 510 m/s
(Table of contents)
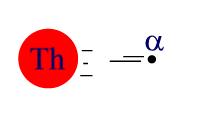
9. An atomic nuclear at rest decays radioactively into an
alpha particle and a smaller nucleus. What will be the speed of this recoiling
nucleus if the speed of the alpha particle is 3.8 x 105 m/s? Assuming
the recoiling nucleus has a mass 57 times greater than that of the alpha
particle.
In the first frame, you have the parent nucleus at rest with
zero momentum, and in the second frame, you have the daughter nucleus
with a mass of 57 m recoiling to the left (-) and the alpha particle (a helium
nucleus) with a mass of m moving to the right (+) at 3.8x105
m/s.
 |
 |
| 0 = |
(57m)v + m(3.8x105
m/s) |
the m divides out of both sides, and you get that the recoil velocity is 57
times smaller and opposite in direction:
v = 6666.666667 (YAAAAAHHHHH!!!) = 6.7x103 m/s opposite direction
of the alpha.
An interesting note is that when we solve these problems of alpha decay (in
chapter 30) we assume that the alpha particle has all the kinetic energy that
the decay releases. This is of course not totally true, as momentum must
be conserved, and so the daughter nucleus must carry away an equal but opposite
momentum and therefore must have some kinetic energy. But it is almost
true, as if we compare the kinetic energies:
KEalpha/KEdaughter
= 1/2m(3.8x105
m/s)2/ 1/257m(6666.666667)2
KEalpha/KEdaughter
= (3.8x105 m/s)2/57(6666.666667)2
KEalpha/KEdaughter
= 57 times which means that the daughter nucleus has 57 times
less the kinetic energy of the alpha particle.
(Table of contents)
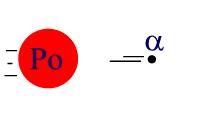
10. An atomic nucleus initially moving at 420 m/s emits
an alpha particle in the direction of its velocity, and the nucleus slows to 350
m/s. If the alpha particle has a mass of 4.0 u and the original nucleus has a
mass of 222 u, what speed does the alpha particle have when it is emitted?
In the first frame, you have the parent nucleus with a mass
of 222u (a u is 1/12 the mass of carbon 12 - about the mass of a nucleon
{neutrons, protons}) bopping along to the right (+) at 420 m/s, and in
the second frame, you have the daughter nucleus with a mass of 218u still
moving in the original direction (+) at 350 m/s, and the alpha particle (a
helium nucleus) with a mass of 4u moving to the right (+) at some
unknown velocity.
 |
 |
| (222u)(420 m/s)
= |
(218u)(350) + (4u)v |
the u divides out of both sides, and you get:
(222)(420 m/s) = (218)(350) + (4)v
v = 4235 m/s = 4.2x103 m/s
(Table of contents)
11. a 13-g bullet traveling 230 m/s penetrates a
2.0-kg block of wood and emerges going 170 m/s. If the block is stationary
on a frictionless surface when hit, how fast does it move after the bullet
emerges?
 |
 |
| (.013 kg)(230
m/s)
= |
(2.0 kg)v +
(.013 kg)(170 m/s) |
In the first frame,
you have the .013 kg bullet going 230 m/s, and in the second frame, the block
of wood (that miraculously has not lost any pieces or changed in mass) going
an unknown velocity, and the bullet going 170 m/s.
Solving for v gives .39 m/s
14. A tennis ball may leave the racket of a top player
on the serve with a speed of 65.0 m/s. If the ball's mass is 0.0600 kg and it is
in contact with the racket for 0.0300 s, what is the average force on the ball?
Would this force be large enough to lift a 60-kg person?
We know that
Impulse = Dp = FDt
and implicitly, Dp = mDv
so ultimately,
FDt = mDv
We know that in .0300 second, a .0600 kg tennis ball undergoes a
change in velocity of 65.0 m/s.
FDt = mDv
F(.0300 s) = (.0600 kg)(65.0 m/s)
F = 130. N, you would need (60 kg)(9.8 N/kg) = 588 N to lift a
person.
(Table of contents)
15. A 0.145-kg baseball pitched at 39.0 m/s is hit on
horizontal line drive straight back toward the pitcher at 52.0 m/s. If the
contact time between bat and ball is 1.00 x 10-3 s, calculate the
average force between the ball and the bat during contact.
We know that
Impulse = Dp = FDt
and implicitly, Dp = mDv
so ultimately,
FDt = mDv
We know that in 1.00x10-3 second, a .145 kg baseball
goes from moving 39 m/s toward the batter, to 52 m/s toward the
outfield. If we make toward the outfield the positive direction, the
initial velocity (toward the batter) is -39 m/s, and the change in velocity of
the ball is 52.0 m/s - (-39.0 m/s) = +91.0 m/s.
(Change is always final minus initial)
FDt = mDv
F(1.00x10-3 s) = (.145 kg)(+91.0 m/s)
F = +13195 N = 1.32x104 N (toward the outfield on
the ball)
(Table of contents)
16. A golf ball of mass 0.045 kg is hit off the tee at
the speed of 45 m/s. The golf club was in contact with the ball for 5.0 x 10-3
s. Find (a) the impulse imparted to the golf ball, and (b) the average force
exerted on the ball by the golf club.
From the HL Data packet:
Impulse = Dp = FDt
and implicitly, Dp = mDv
So the Impulse imparted to the ball by the club is
Dp = mDv = (.045 kg)(45 m/s)
= 2.025 kgm/s = 2.0 kgm/s
To find the force,
FDt = mDv
We know that in 5.00x10-3 second, a .045 kg golf ball
undergoes a change in velocity of 45 m/s. (Change is always final minus
initial, and I am making the direction of the original pitch positive)
FDt = mDv
F(5.00x10-3 s) = (.045 kg)(45 m/s)
F = 405 N
(Table of contents)
18. A 115-kg fullback is running at 4.0 m/s to the east
and is stopped in 0.75s by a head on tackle by a tackler running due west.
Calculate (a) the original momentum of the fullback, (b) the impulse exerted on
the fullback, (c) the impulse exerted in the tackler, and (d) the average force
exerted on the tackler.
Let's make to the East the positive direction. Since
the Fullback is running toward the East (+4.0 m/s), and is stopped, the
change in velocity is -4.0 m/s.
The original momentum of the fullback:
p = mv = (115 kg)(4.0 m/s) = 460 kgm/s (East)
Since the Fullback is running toward the East (+4.0 m/s), and is stopped,
the change in velocity is -4.0 m/s.
Since
Impulse = Dp = FDt, then the
impulse exerted on the Fullback is
Dp = mDv = (115
kg)(-4.0 m/s) = -460 kgm/s (West) - so to stop something going to the East,
you exert a force to the West. Radical.
The tackler would undergo a change in momentum due to the reaction force,
which would be exactly equal, but opposite, according to Newton's third
law. So the tackler would have the opposite impulse exerted on them as
the Fullback:
Dp = 460 kgm/s (East)
And to find the force exerted on the tackler:
Impulse = Dp = FDt
460 kgm/s = F(.75 s)
F = 613.3 N = 610 N
(Table of contents)















