Problem Set 5.3: | 1
| 2 |
3 | 4 | 5
|
7 | 8 | 9
| 11 | 12 | 13 | 18
| 21 | Go up
- by Cooper Spear, Sonja Scherer, To Chong, and Chris
Murray, 2001
1. A jet plane traveling 1800 km/h (500 m/s) pulls out of a dive by moving in an arc of radius 6.00 km. What is the plane's acceleration in g's?
Obviously, use the velocity in m/s, and 6.00 km = 6000m, so
The plane's acceleration is:
a = v2/r = (500 m/s)2/(6000 m) = 41.67 m/s2
But they wanted it in "g"s, so we divide by (9.8 m/s/s)/"g":
41.67/9.8 = 4.25 "g"
(Table of contents)
2. A child on a merry-go-round is moving with a speed of 1.35 m/s when 1.20 m from the center of the merry-go-round. Calculate (a) the centripetal acceleration of the child, and (b) the net horizontal force exerted on the child (mass = 25.0 kg).
(a) The centripetal acceleration of the child will be:
a = v2/r = (1.35 m/s)2/(1.2 m) = 1.52 m/s2(b) The net horizontal force exerted on the child:
F = ma = (25 kg)(1.52 m/s/s) = 38 N
(Table of contents)
3. Calculate the centripetal acceleration of the Earth in its orbit around the sun and the net force exerted on the Earth? What exerts this force on the Earth? Assume that the Earth's orbit is a circle of radius 1.50 x 1011 m.
The period which the Earth orbits around the Sun is: (365.26 day)(24 hr/day)(3600 s/hr) = 31558464 s
The centripetal acceleration of the Earth in its orbit around the sun will be: a = v2/r = (2πr/T)2/r = 4π2r/T2
Then a = 4π2 (1.5x1011m)/(31558464 s)2 = 0.005946 m/s2 = .0059 m/s/s toward the Sun.We know that the mass of Earth is 5.98 x 1024 kg. So the net force exerted on the Earth is: F = ma
F = (5.98 x 1024 kg)(0.005946 m/s2) = 3.55566x1022 N = 3.6 x 1022 N toward the Sun
(Table of contents)
4. A horizontal force of 280 N is exerted on a 2.0-kg discus as it is rotated uniformly in a horizontal circle (at arms length) of radius 1.00 m. Calculate the speed of the discus.
The relationship between the centripetal force, radius of curvature, and velocity of the object is: F = ma = mv2/r. (We will discus this further in class!!!!!!!!!)
Let's solve this expression for the velocity:
F = mv2/r
Fr = mv2
Fr/m = v2
Hence, v = (rF/m)1/2 = [(1.00 m)(280 N)/(2.0 kg)]1/2 = 12 m/s
(Table of contents)
5. A flat puck (mass M) is rotated in a circle on a frictionless air hockey table top, and is held in this orbit by a light cord which is connected to a dangling mass (mass m) through the central hole as shown in Fig. 5-32. Show that the speed of the puck is given by v = Ö(mgR/M)
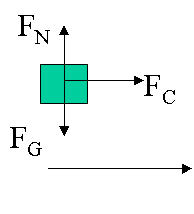
The forces exerted on the puck (M) are force of gravity, normal force and centripetal force. Since it is resting on the table, the force of gravity is cancelled by the normal force exerted by the table. (i.e. the table is holding it up) Thus, according to Newton's second law, we have: FC = Ma = Mv2/R
In the other hand, we apply Newton's second law for the dangling mass (m).
FG – FC = 0
FC = FG = mgSo we have: Mv2/R = mg
Solving for v:
Mv2/R = mg
v2 = mgR/M
And finally v = Ö(mgR/M)
(Table of contents)
7. What is the maximum speed with which a 1050-kg car can round a turn of radius 70 m on a flat road if the coefficient of friction between tires and road is 0.80? Is this result independent of the mass of the car?
Maximum velocity:
The weight of the car is (1050 kg)(9.80 N/kg) = 10290 N.
The maximum force of friction between the tires and the road is
Ffr £ µsFN
So Ffr £ (.80)(10290 N) = 8232 N
This causes a centripetal acceleration of:
F = ma
8232 N = (1050 kg)a
a = 7.84 m/s/s
And since a = v2/r,
7.84 m/s/s = v2/(70. m), v = 23.4265 m/s = 23 m/sIs this result independent of the mass of the car?
There are three forces exerting on the car which be analyzed above. On the axis x we have:
Ffr = ma = mv2/r
Ffr =< µmg then Ffr has the maximum value when and only when Ffr = µmg
So the maximum speed of the car will be:
µmg = mv2/r - Divide both sides by m:
µg = v2/r
Since the mass cancels out, the result is not dependent on the mass.
v = (grm)1/2 = (9.8*70*0.8)1/2 = 23.43 m/s2
Yes, the result is independent of the mass.
(Table of contents)
8. A ball on the end of a string is cleverly revolved at a uniform rate in a vertical circle of radius 85.0 cm, as shown in Fig. 5-33. If its speed is 4.15 m/s and its mass is 0.300 kg, calculate the tension in the string when the ball is (a) at the top of its path, and (b) at the bottom of its path.
The radius of the mass in meters is .85 m
The acceleration of the .300 kg mass is v2/r = (4.15 m/s)2/(.85 m) = 20.2618 m/s/s
The weight of the .300 kg mass is (.300 kg)(9.8 N/kg) = 2.94 N
(a) At the top we have the weight downward (-), the tension FT1 acting (down???), and a downward (-) acceleration of 20.2618 m/s/s. The acceleration is downward because it is toward the center, and when you are at the top, the center is below you. So F = ma looks like:
<FT1 - 2.94 N> = (.300 kg)(-20.2618 m/s/s)
FT1 = -3.1385 N = 3.14 N Down
(b) At the bottom we have the weight downward (-), the tension FT2 acting (up???), and an upward (+) acceleration of 20.2618 m/s/s. The acceleration is upward because it is toward the center, and when you are at the bottom, the center is above you. So F = ma looks like:
<FT2 - 2.94 N> = (.300 kg)(+20.2618 m/s/s)
FT2 = 9.0185 N = 9.02 N Up
(Table of contents)
9. How large must the coefficient of friction be between the tires and the road if a car is to round a level curve of radius 85 m at a speed of 95 km/h?
First, convert the annoying km/hr to m/s:
95km/h/3.6 = 26.38888889 m/s
The force of friction is making the car go around the corner, so we will set the formula for friction:
Ffr = µFN = µmg
Equal to the centripetal force:
F = m4π2r/T2
Finally:
µmg = mv2/r
So, let's solve for µ:
µmg = mv2/r
µg = v2/r
µ = v2/rg
µ = (26.38888889 m/s)2/(85 m)(9.80 m/s/s) = 0.836 = .84 or larger
(Table of contents)
11. A coin is placed 11.0 cm from the axis of a rotating turntable of variable speed. When the speed of the turntable is slowly increased, the coin remains fixed on the turntable until a rate of 36 rpm is reached, at which point the coin slides off. What is the coefficient of static friction between the coin and the turntable?
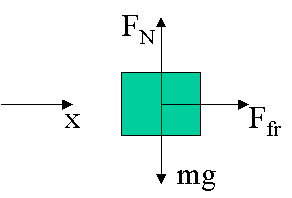
The force of friction is making the coin go in circles, so we will set the formula for friction:
Ffr = µFN = µmg
Equal to the centripetal force:
F = m4π2r/T2
Finally:
µmg = m4π2r/T2
So, let's solve for µ:
µmg = m 4π2r/T2
µg = 4π2r/T2 (m cancels out)
µ = 4π2r/gT2 (divide both sides by g)
Well, r = 11.0 cm = .110 m, but what is the velocity?
The problem says the rotational velocity is 36 RPM, which means 36 Revolutions Per Minute. So the 60 seconds of a minute are divided into 36 equal parts, and the time for one revolution, or the period T is (60 s/min)/(36 rev/min) = 1.6667 sec/rev
So let's plug back into the master equation:
µ = 4π2r/gT2 = 4π2(.110 m)/(9.80 m/s/s)(1.6667 s)2 = 0.1595 = .16
(Table of contents)
12. At what maximum speed must a roller coaster be traveling when upside down at the top of a circle (Fig. 5-34) if the passengers are not to fall out? Assume a radius of curvature of 8.6 m.
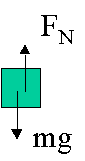
The maximum speed at which the passenger won't fall down must satisfy: mv2/r = FG (The centripetal force just equals the force of gravity). At that time normal force is equal 0 - the passengers are weightless for an instant.
mv2/r = FG
mv2/r = mg
v2/r = g
v = Ö (rg) = Ö[(8.6 m)((9.80 m/s/s)]) = 9.1804 m/s = 9.2 m/s
(Table of contents)
13. A 1000-kg sports car moving at 20 m/s crosses the rounded top of a hill (radius = 100 m). Determine (a) the normal force on the car, (b) the normal force on the 70-kg driver, and (c) the car speed at which the normal force equals zero.
This is a well disguised motion in a vertical circle problem. The centripetal acceleration of the car is given by v2/r :
a = v2/r = (20. m/s)2/(100. m) = 4 m/s/s. At the crest of the hill, the centripetal acceleration would be downward because the center of the circle would be below the car, and centripetal acceleration is toward the center.
The car has a weight of (1000 kg)(9.80 N/kg) = 9800 N, and so the expression of Newton's second law at the top of the hill is shaping up. We have the weight down (-), the acceleration down (-) and the normal force of the road FN (up???) so F = ma looks like:
<FN - 9800 N> = (1000 kg)(-4.0 m/s/s) = 5800 N
The driver has a weight of (70 kg)(9.80 N/kg) = 686 N, and so we have the weight down (-), the acceleration down (-) and the normal force of the car FN (up???) so F = ma looks like:
<FN - 686 N> = (70 kg)(-4.0 m/s/s) = 406 N = 410 N
The normal force will be zero (and the car will take some air!!!) when its centripetal acceleration is equal to 9.8 m/s/s
a = v2/r
ar = v2
Ö(ar) = v
So v = Ö(ar) = Ö[(9.80 m/s/s)(100. m)] = 31.3050 = 31.3 m/s
(Table of contents)
18. In a "Rotor-ride" at a carnival, people pay money to be rotated in a vertical cylindrically walled "room". (See Fig. 5-36.) If the room radius is 5.0 m, and the rotation frequency is 0.50 revolutions per second when the floor drops out, what is the minimum coefficient of static friction so that people will nit slip down? People describe this ride by saying they were being "pressed against the wall". Is this true? Is there really an outward force pressing them against the wall? If so, what it is source? If not, what is the proper description of their situation (besides "scary")? (Hint: First draw the free-body diagram for a person.)
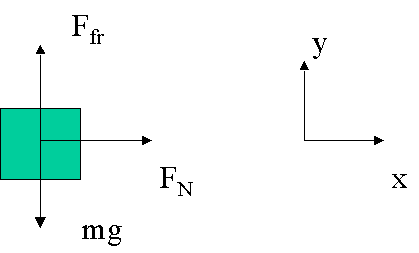
If it goes halfway around in one second, then the period of the ride must be 2.0 seconds.
What is going on is that the ride is pushing on the people to make them go in a circle. For every action there is an equal but opposite reaction, and so the people push back on the ride. The centripetal force the ride exerts on people becomes the normal force that causes the friction that keeps them from sliding down the walls, and that friction as such must be larger than their weight, or down the wall they go. There is nothing pushing them to the outside, rather they are accelerating toward the middle of the circle. Remember that you feel "thrown" the opposite direction of the acceleration. (i.e. if your car accelerated forward, you are thrown backward)
So, the normal force is just the centripetal force acting on the people: (I pick the centripetal force with the period in it)
FN = m4π2r/T2
Since the friction force must be larger than or equal to the weight of the riders, the minimum coefficient of static friction will be:
mg = Ffr = µFN = µ(m4π2r/T2)
And if you plug the centripetal force in for the normal force, you get:
mg = µ(m4π2r/T2) - so let's solve for µ:
g = µ(4π2r/T2) (canceling the mass)
gT2/(4π2r) = µ (divide both sides by 4π2r/T2)
µ = gT2/(4π2r) = (9.80 m/s/s)(2.0 s)2/[4π2(5.0 m)] = .1986 = .20
(Table of contents)
21. A pilot performs an evasive maneuver by diving vertically at 310 m/s. If he can withstand an acceleration of 9.0 g's without blacking out, at what altitude must he begin to pull out of the dive to avoid crashing into the sea?

The centripetal acceleration is 9.0 "g"s which is (9.0)(9.8 m/s/s) = 88.2 m/s/s. Basically, the question is what radius circle has a centripetal acceleration of 88.2 m/s/s when you are flying at 310 m/s:
a = v2/r
r = v2/a = (310 m/s)2/(88.2 m/s/s) = 1089.5692 m = 1100 m = 1.1 km
(Table of contents)
Just a walkin' down the street
singin' dooh wah ditty
ditty dum ditty doo