Problem Set 3.7: | 1
| 5 |
7 | 9 | 11 | 13
|
15 | 19 | 22 | 21
| 24 | 27 | 29 | 31
| 32 | Go up
- by To To Chong, Cooper
Spear, and Chris Murray Oct/2001
1. A car is driven 125 km west and then 65 km
southwest. What is the displacement of the car form the point of origin
(magnitude and direction)? Draw a diagram.
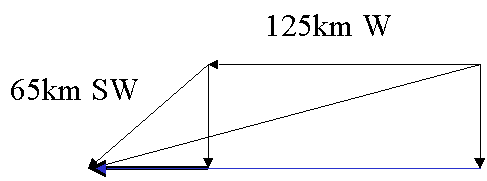

y1 = 0
x1 = -125km
y2 = -65cos45 = -46km
x2 = -65sin45 = -46km
x = x1 + x2 = -125km - 46km = -171km
y = y1 + y2 = -46km
The displacement of the car is: D2 = x2 + y2
è
D = ((46 km)2 + (171 km)2)1/2 = 177km
tan@ = 46/171 = 0.27 ==> @ =15degree South of West
(Table of contents)
5. Graphically determine the resultant of the following
three vector displacements: (1) 24 m, 30° north of east; (2) 28m 37° east of
north; and (3) 20 m, 50° west of south?
Here is what those vectors look like:

Now, they are asking us to add these vectors graphically, which would look
like:

Where the black vector is the resultant.
But we can do better than that
Vector 1 has these components, both positive:
x1 = 24cos30 = 20.78m
y1 = 24sin30 = 12m
Vector 1 = 20.78 m x + 12 m y
Vector 2 has these components, both positive:
x2 = 28sin37 = 16.85m
y2 = 28cos37 = 22.36m
Vector 2 = 16.85 m x + 22.36 m y
Vector 3 has these components, both negative:
x3 = 20sin50 = 15.32m
y3 = 20cos50 = 12.86m
Vector 3 = -15.32 m x + -12.86 m y
The sum of these three would be:
| Vector |
X direction |
Y direction |
| 1 |
20.78 m x + |
12 m y |
| 2 |
16.85 m x + |
22.36 m y |
| 3 |
-15.32 m x + |
-12.86 m y |
| Sum: |
22.31 m x + |
21.5 m |
The resultant is: D = (x2 + y2)1/2 =
31m
The angle is tan-1(21.5/22.31) = 44 degrees North
of East
(Table of contents)
7. Figure 3-33 shows two vectors, A and B,
whose magnitudes are A=8.31 units and B=5.55 units.
Determine C if (a) C=A+B, (b) C=A-B, (c)
C=B-A. Give the magnitude and direction for each.

This is baby hard. A, since it is to the right would
be 8.31 x + 0 y, and B, since it is to the left, would be -5.55 x + 0 y.
So A+B:
|
A: |
8.31 x + 0 y
|
| + |
B: |
-5.55 x + 0 y
|
| = |
|
2.76 x + 0 y |
A-B:
|
A: |
8.31 x + 0 y
|
| - |
B: |
-5.55 x + 0 y
|
| = |
|
13.86 x + 0 y |
B-A:
|
B: |
-5.55 x + 0 y
|
| - |
A: |
8.31 x + 0 y
|
| = |
|
-13.86 x + 0 y |
(Table of contents)
9. A airplane is traveling 785 km/h in a direction 38.5°
west of north (Fig. 3-34). (a) Find the components of the velocity
vector in the northerly and westerly directions. (b) How far north
and how far west has the plane traveled after 3.00 h?
Let's break the vector into components first:

The Westward component is found with the Sin, and the
Northerly component is found with Cos:
VWest = (785 km/hr)sin(38.5o) = 488.67 km/hr = 489 km/hr
VNorth = (785 km/hr)cos(38.5o) = 614.35 km/hr = 614 km/r
To find out how far in 3.00 hr, just multiply by time:
v = s/t, s = vt:
SWest = (488.67 km/hr)(3.00 hr) = 1470 km
VNorth = (614.35 km/hr)(3.00 hr) = 1840 km
(Table of contents)
11.Three vectors are shown in Fig. 3-35. Their
magnitudes are given in arbitrary units. Determine the sum of the three
vectors. Give the resultant in terms of (a) components, (b)
magnitudes and angle with x axis.

First let's find the components:
Vector A has two positive components, the x is found with Cos since it
is adjacent to the angle, and the y is found with Sin:
A = +(66.0)Cos(28.0o) + (66.0)Sin(28.0o)
A = 58.27 x + 30.99 y
Vector B has a negative x component (goes to the left), and a positive y
component (goes up). The x is adjacent to the angle, and so we use Cos,
and the y is again opposite, so we use Sin:
B = -(40.0)Cos(56.0o) + (40.0)Sin(56.0o)
B = -22.37 x + 33.16 y
Vector C is easy, it is all in the -y direction (it goes down), so
C = 0 x + -46.8 y
So let's add them up like we're told:
| Vector |
X direction |
Y direction |
| A |
58.27 x + |
30.99 y
|
| B |
-22.37 x + |
33.16 y |
| C |
0
x + |
-46.8 y |
| Sum: |
35.9
x + |
17.35 y
|
Now we are ready to turn it into an Angle Magnitude vector:
Draw the new vector:

Find the magnitude:
hyp = Ö{(35.9)2
+ (17.35)2} = 39.9
The angle between the x axis (blue) and the vector (black) is the inverse
tangent of opposite over adjacent:
q
=Tan-1{17.35/35.9} =
25.8o
(Table of contents)
13. (a) Given the vectors A and B
shown in Fig. 3-35, determine B-A. (b) Determine A-B
without using your answer in (a). Then compare your results and see
if they are opposite.

First let's find the components:
Vector A has two positive components, the x is found with Cos since it
is adjacent to the angle, and the y is found with Sin:
A = +(66.0)Cos(28.0o) + (66.0)Sin(28.0o)
A = 58.27 x + 30.99 y
Vector B has a negative x component (goes to the left), and a positive y
component (goes up). The x is adjacent to the angle, and so we use Cos,
and the y is again opposite, so we use Sin:
B = -(40.0)Cos(56.0o) + (40.0)Sin(56.0o)
B = -22.37 x + 33.16 y
So first find B - A:
B - A is the same as B + (-A), and since A = 58.27 x + 30.99 y, -A =
-58.27 x + -30.99 y
So let's add -A to B:
| Vector |
X direction |
Y direction |
| A |
-58.27 x + |
-30.99 y
|
| B |
-22.37 x + |
33.16 y |
| Sum: |
-80.64 x + |
2.17 y |
Now we are ready to turn it into an Angle Magnitude vector:
Draw the new vector:

Find the magnitude:
hyp = Ö{(80.64)2
+ (2.17)2} = 80.7
The angle between the x axis (blue) and the vector (black) is the inverse
tangent of opposite over adjacent:
q
=Tan-1{2.17/80.64} =
1.54o
Now let's find A - B:
A - B is the same as A + (-B), and since B = -22.37 x + 33.16 y, -B = +22.37 x
+ -33.16 y
So let's add -A to B:
| Vector |
X direction |
Y direction |
| A |
58.27 x + |
30.99 y
|
| B |
+22.37 x + |
-33.16 y |
| Sum: |
80.64 x + |
-2.17 y |
Now we are ready to turn it into an Angle Magnitude vector:
Draw the new vector:

Find the magnitude:
hyp = Ö{(80.64)2
+ (2.17)2} = 80.7
The angle between the x axis (blue) and the vector (black) is the inverse
tangent of opposite over adjacent:
q
=Tan-1{2.17/80.64} =
1.54o
And, by golly, this is exactly opposite B - A.
(Table of contents)
15.For the vectors shown in Fig, 3-35, determine (a)
C-A-B, (b) 2A-3B+2C.

First let's find the components:
Vector A has two positive components, the x is found with Cos since it
is adjacent to the angle, and the y is found with Sin:
A = +(66.0)Cos(28.0o) + (66.0)Sin(28.0o)
A = 58.27 x + 30.99 y
Vector B has a negative x component (goes to the left), and a positive y
component (goes up). The x is adjacent to the angle, and so we use Cos,
and the y is again opposite, so we use Sin:
B = -(40.0)Cos(56.0o) + (40.0)Sin(56.0o)
B = -22.37 x + 33.16 y
Vector C is easy, it is all in the -y direction (it goes down), so
C = 0 x + -46.8 y
So let's put them into a happy fun table:
| Vector |
X direction |
Y direction |
| A |
58.27 x + |
30.99 y
|
| B |
-22.37 x + |
33.16 y |
| C |
0
x + |
-46.8 y |
Our first task is to find C - A - B, (Which spells
CAB.....Coincidence??? I THINK NOT!!!!!!!!)
I am just going to add C, -A and -B together:
| Vector |
X direction |
Y direction |
| -A |
-58.27 x + |
-30.99 y
|
| -B |
+22.37 x + |
-33.16 y |
| C |
0
x + |
-46.8 y |
| Sum: |
-35.9 x + |
-110.95 y |
Now we are ready to turn it into an Angle Magnitude vector:
Draw the new vector:

Find the magnitude:
hyp = Ö{(35.9)2
+ (110.95)2} = 117
The angle between the x axis (blue) and the vector (black) is the inverse
tangent of opposite over adjacent:
q
=Tan-1{110.95/35.9} =
72.1o
Our second task is to find 2A - 3B + 2C,
I am just going to add 2A, -3B, and 2C together:
Since A = 58.27 x + 30.99 y,
2A = 2(58.27 x + 30.99 y) = 116.54 x + 61.98 y
B = -22.37 x + 33.16 y,
-3B = -3(-22.37 x + 33.16 y) = 67.11 x + -99.48 y
C = 0 x + -46.8 y,
2C = 2(0 x + -46.8 y) = 0 x + -93.6 y
So let's add them together:
| Vector |
X direction |
Y direction |
| 2A |
116.54 x + |
61.98 y |
| -3B |
67.11 x + |
-99.48 y |
| 2C |
0
x + |
-93.6 y |
| Sum: |
183.65 x + |
-131.1 y |
Now we are ready to turn it into an Angle Magnitude vector:
Draw the new vector:

Find the magnitude:
hyp = Ö{(183.65)2
+ (131.1)2} = 226
The angle between the x axis (blue) and the vector (black) is the inverse
tangent of opposite over adjacent:
q
=Tan-1{131.1/183.65}
=35.5o
(Table of contents)
19. A tiger leaps horizontally form a 7.5-m-high rock
with a speed of 4.5 m/s. How far from the base of the rock will she land?

| Horizontal |
Vertical |
s =
u = 4.5 m/s
v = "
a = 0
t = |
s = -7.5 m
u = 0 (Purely horizontal)
v = ? (don't care!)
a = -9.8 m/s/s
t = ? |
| |
Use
s = ut + 1/2at2
-7.5 = 1/2(-9.8)t2
t = 1.2372 s |
| Use:
vav = Ds/Dt,
as we now know t
4.5 m/s = s/(1.2372s)
s = 5.567 m = 5.6m |
|
(Table of contents)
22. Romeo is chucking pebbles gently up to Juliet's
window, and he wants the pebbles to hit the window with only a horizontal
component of velocity. He is standing at the edge of a rose garden 8.0 m
below her window and 9.0 m from the base of the wall (Fig. 3-38). How
fast are the pebbles going when they hit her window?
| Horizontal |
Vertical |
s = 9.0 m
u = ???
v = "
a = 0
t = |
s = 8.0 m
u = ?
v = 0 (final is purely horizontal)
a = -9.8 m/s/s
t = ? |
| From the vertical we've got: t = 1.278s |
Use
v2 = u2 + 2as
0 = u2 + 2(-9.8)(8.0)
u = 12.522m/s
|
| The horizontal velocity is: x = ut = vt
v = x/t = 9/1.278 = 7m/s
|
v = u + at
t = u/g = 12.522/9.8 = 1.278s
|
| As the vertical final velocity is zero, the velocity of
the pebble when it hits the windows is:
V = (Vx2 + Vy2)1/2 =
(02 + 72)1/2 = 7m/s
|
|
(Table of contents)
21. A fire hose held near the ground shoots water at a
speed of 6.5 m/s. At what angle(s) should the nozzle point in order that the
water land 2.0 m away (Fig. 3-37) ? Why are there different angles?
use the range equation (range = v2sin(2q)/g)
The necessary angle is:
sin2@ = (Rg)/v2 = (2 * 9.8)/6.52 =
0.464 ==> 2@ = 27.640 è
@ = 140
Or @ = 900 – 140 = 760
We've got two different angle because:
- At the larger angle the water has a smaller horizontal
velocity but spends more time in the air, because of the larger initial
vertical velocity, thus the horizontal displacement is the same for the two
angles.
(Table of contents)
24. A ball is thrown horizontally from the roof of a
building 56 m tall lands 45 m from the base . What was the ball's initial speed?
| Horizontal |
Vertical |
s = 45 m
u = ???
v = "
a = 0
t = ? |
s = -56 m
u = 0 (purely horizontal)
v = ?
a = -9.8 m/s/s
t = ? |
| The ball's initial speed is horizontal. So we have:
s = vt = ut
==> u = s/t = 45/3.38 = 13.31m/s
|
Use s = ut + 1/2at2
t = (2s/g)1/2 = (2 * 56/9.8)1/2 = 3.38s
|
| |
|
(Table of contents)
27. A ball thrown horizontally at 22.2 m/s from the roof
of a building lands 36.0 m from the base of the building. How high is the
building?
Choose the coordinate system Oxy like this, then we have:
| Horizontal |
Vertical |
s = 36.0 m
u = 22.2 m/s
v = "
a = 0
t = ? |
s = ????
u = 0 (purely horizontal)
v = ?
a = g = 9.8 m/s/s
t = ? |
| x = vt = ut
t = x/u = 36/22.2 = 1.6216s
|
|
| |
The height of the building is:
s = ut + 1/2at2
y0 = 0
s = 1/2gt2 = ½ * 9.8 * 1.62162
= 12.9m |
(Table of contents)
29. Determine how much farther a person can jump on the
Moon as compared to the Earth if the takeoff speed and angle are the same. The
acceleration due to gravity on the Moon is one-sixth what is on the earth.
Use the range equation (range = v2sin(2q)/g)
Suppose the takeoff speed is u, the angle is @.
Due to the exercise, we have this: gM = 1/6gE
RE = (u2sin2@)/gE
RM = (u2sin2@)/gM
RM/RE = gE/gM
= 6
So it is 6 times farther in the moon.
(Table of contents)
31. The pilot of an airplane traveling160 km/h wants to
drop supplies to flood victims isolated on a patch of land 160 m below. The
supplies should be dropped how many how many seconds before the plane is
directly overhead?
| Horizontal |
Vertical |
s = 36.0 m
u = 160/3.6 = 44.4444 m/s (not used)
v = "
a = 0
t = ? |
s = -160 m
u = 0 (purely horizontal)
v = ?
a = -9.8 m/s/s
t = ?????? |
| |
Use s = ut + 1/2at2
-160 = 0 + 1/2(-9.8)t2 So t = 5.714 s = 5.7
s |
(Table of contents)
32. A hunter aims directly at a target (on the same
level) 120 m away. (a) If the bullet leaves the gun at a speed of 250 m/s, by
how much will it miss the target? (b) At what angle should the gun be
aimed so the target will be hit?
a.
| Horizontal |
Vertical |
s = 120 m
u = 250 m/s
v = "
a = 0
t = ? |
s = ????
u = 0 (purely horizontal)
v = ?
a = -9.8 m/s/s
t = ? |
Use:
vav = Ds/Dt
250 m/s = 120 m/t,
t = .48 s
|
|
| |
Use s = ut + 1/2at2 s =
0 + 1/2(-9.8)(.48)2 = 1.129 = 1.1
m |
b. use the range equation (range = v2sin(2q)/g)
so
q
= sin-1(g(range)/v2)/2
= .539 = .54o above horiz
(Table of contents)









