IB Problem Set 17: | 1
| 3 |
5 | 7 | 11 | 15
| 17
|
19 | 21 | AP#4 | Go up
- by Will Gannett, class of 2002, IB Physics HL
1. How much work is needed to move a -8.6mC
charge from ground to a point whose potential is +75V?
Well, I know that the equation to use is W=qV, where W is
work in joules, q is charge in Coulombs (sp?), and V is voltage in
Volts. q is obviously -8.6mC
(-8.6E-6 C), and V will be 75, since it has to go from the ground (0V)
to the point (75V). Since the charge is negative and it is being moved
from 0V to 75V, we know that any work done in this case will not be work
required from an external source, but work done by the field itself (in the
form of electrostatic potential energy being converted to kinetic
energy). The amount of work done will be W=qV=-8.6E-6*75=-6.45E4J.
Again, this in negative to show that it is work done by the field rather than
work required.
(Table of contents)
3. How much kinetic energy will an electron gain (in
joules and eV) if it falls through a potential difference of 21,000V in a TV
picture tube?
There are two ways to do this problem. One will give
you the answer in eV, and one will give you the answer in joules.
Neither are difficult. The first way is the more complicated, and uses
the formula from the previous question, W=qV. V=21000, the potential
difference, and q is the charge of one electron, or 1.602E-19C.
Therefore, the work (which will all be converted to kinetic energy) is
21000*1.602e-19=3.4E-15J. To get the answer in eV is much easier.
We know that it is one electron being accelerated through 21000V.
Therefore, the total number of electron Volts will be 21000, or 21keV.
(Table of contents)
5. How strong is the electric field between two parallel
plates 5.2mm apart if the potential difference between them is 220V?
Well, you should know that there are two different
units for electric field strength: either N/C, or V/m. These are both in
the data packet, as E=F/q and E=-DV/Dx.
E=-DV/Dx is obviously
the one to use here.
E=-DV/Dx
E=-220/5.2E-3
E=-42000V/m
The sign of the answer only shows the direction of the field.
(Table of contents)
7. What potential difference is needed to give a helium
nucleus (Q=2e) 65.0keV of KE?
We know that a single electron, moved through V volts, will
gain V electron volts of energy. Similarly, 2 electrons (or an object
with the same charge as two electrons, such as a helium nucleus) will gain 2V
electron volts of energy when moved through V volts. From this, we can
see that an object with a charge of two electrons (or protons) that has
65000eV of energy would have to only be accelerated through half the voltage a
single electron would have been. This means that the answer is 65000/2,
or 32500V. To do the math:
65000eV/2e=32500V.
(Table of contents)
11. What is the speed of a proton whose kinetic energy is
28.0 MeV?
I think that the easiest way to do this would be to use the
equation W=.5*m*v2. First, we must convert 28.0MeV to
joules. This is a simple matter.
28.0E6eV*1.602e-19C/e
=4.49E-12VC
=4.49E-12J
So, the proton has 4.49E-12 joules of kinetic energy. Since we know the
mass of the proton (1.67e-27kg, for those of you too lazy to actually look at
your data packet), it is another simple matter to solve for the velocity.
W=.5*m*v2
4.49E-12=.5*1.67E-27*v2
4.49E-12/.5/1.67E-27=v2
v2=5.38E15
SO, v=7.33E7ms-1
(Table of contents)
15. A +30 micro coulomb charge is placed 32 cm from
an identical +30 micro coulomb charge. How much work would be required to
move a +0.50 micro coulomb charge from a point midway between them to t point 10
cm closer to either of the two charges?
All we need to do is multiply the test charge by the change
in voltage. V = W/q, so the work, W = Vq where V is the change in
voltage, and q is the charge moved.
We now have two locations, one directly between the two +30
micro coulomb charges, that is 16 cm from each of them, since they are 32 cm
apart, and a second location that is 6 cm from one of the charges, and 26 cm
from the other. See the diagram below:
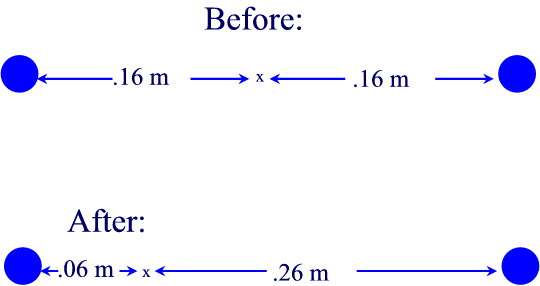
So to solve these problems you just do these three steps:
1. Find the voltage before and after the move
2. Find the difference in voltage (subtract)
3. Use W = Vq to calculate the work done
So the voltage before is simply V = kq/r + kq/r (yay no vectors)
Vbefore = 8.99e9(30e-6)/.16 +
8.99e9(30e-6)/.16 = 3371250 V
and after it is: (note the distances are the only things
that change)
Vafter = 8.99e9(30e-6)/.06 +
8.99e9(30e-6)/.26 = 5532307.692 V
The change is that we went up in voltage from 3371250 V to
5532307.692 V, a change of 2161057.692 volts.
Since we are moving a charge of 0.50 micro coulombs through this difference,
the work is simply
W = Vq, W = (2161057.692 V)(0.50e-6 C) = 1.08 J
(Table of contents)
17. How much voltage must be used to accelerate a proton
(radius 1.2 x 10-15 m) so that it has sufficient energy to penetrate
a silicon nucleus? A silicon nucleus has a charge of +14e and its radius
is about 3.6 x 10-15 m. Assume the potential is that for point
charges.
Well, let's first say that the nucleus is stationary and the
proton free. We know that the point at which it will begin to penetrate
is equal to the radius of the silicon nucleus plus the radius of proton.
This is 1.2E-15+3.6E-15, which is 4.8E-15m. Since the proton is only
able to get this close to the nucleus from kinetic energy, it makes sense that
whatever potential energy it now has due to proximity must have been obtained
from the voltage potential. Since the charge on the proton remains the
same and it has no kinetic energy both at the beginning and the end (it starts
out at rest and ends at rest, due to the voltage potential from the charge of
the nucleus), the voltage at those points must be the same (i.e. the voltage
difference from the start to the point of penetration is zero). What we
want to find is the voltage at that point, which will be the same as the
voltage potential through which the proton was accelerated. To do this,
we use the equation V=kq/r.
V=8.99e9*14*1.602E-19/4.8E-15
V=4.2E6=4.2MV
You will notice that the mass and charge of the particle are not
relevant. This implies that this would work with alpha particles as
well, except for the fact that the radius would be different. However,
an alpha particle accelerated through that voltage would travel to the same
distance from the silicon nucleus.
(Table of contents)
19. Consider point a which is 70 cm north of a
-3.8mC
point charge, and point b which is 80 cm west of the charge (Fig.
17-23 in Giancoli). Determine (a) Vba = Vb -
Va and (b) Eb - Ea (magnitude and
direction).
(a) Ok, first we need to find Vb and Va
using V=kq/r
Vb=8.99E9*-3.8E-6/0.8=-42703V
Va=8.99E9*-3.8E-6/0.7=-48803V
So, Vba=-42703--48803=6100V
(b) The electric field is a bit more complicated. We will use a vector
at each point to represent the electric field strength there and calculate the
field strength using E=kq/r2. At point b,
E=8.99E9*-3.8E-6/0.82=-53378N/C. Since a positive charge
placed at point b will travel to the right (it is to the left of a negative
charge), we know that the vector will only have an x-component, and it will be
positive. So, the field at that point is represented by 53378x+0y.
The point b is similar. E=8.99E9*-3.8E-6/0.72=-69718N/C.
The vector at that point will only have a negative y-component, so the vector
will be 0x+-69718y.
Moving to the next step, Eb-Ea =
(53378-0)x+(0--69718)y=53378x+69718y, in vector component form. (Isn't
this great? It's just a chapter 2 problem in disguise!!) The
question asks for the answer in angle-magnitude form, though. So, we
need to convert. The magnitude is easy. It's just the Pythagorean
theorem. 533782+697182=c2, so
c=87806N/C. As for the direction, tan-1(69718/53378)=53º
from vertical, up and to the right. So in conclusion, the answer is
8.8E4N/C, 53° E of N.
(Table of contents)
21. Two identical +7.5mC?
point charges are initially spaced 5.5 cm from each other. If they are
released at the same instant from rest, how fast will they be moving when they
are very far away from each others? Assume they have identical masses of
1.0 mg.
To calculate this, we will use electrostatic potential
energy.
Now, we know that Epot=Ekin, because energy is
conserved, and the potential energy of the system will equal the amount of
work required to put the charges in their current state. We also know
that V=kq/r and V=W/q. So, since kq/r=W/q, W must equal kq2/r.
W=kq2/r
W=8.99E9*(7.5E-6)2/0.055
W=9.194J
So the total energy of the system is 9.194 joules. Since both charges
have the same mass, and momentum is conserved, they will have equal and
opposite velocities. To find these, we use good old 1/2*m*v2.
Also, because they have the same mass, they will end up with the same amount
of energy, 9.194/2, or 4.597J.
1/2*1E-6*v2=4.597
v2=4.597*2/1E-6
v2=9.194E6
v=3.0E3m/s
(Table of contents)
AP # 4 goes Here?
<solution goes here>
(Table of contents)
