Problem Set 16: | 1 | 3 | 5 | 7 | 9 | 11 | 12 | 13 | 15 | 19 | 21 | 23 | 25 | 27 | 30 | 31 | 45 | 51 | Go
up
- by D-Fresh Shriver and P-shizzle Pham,
Gimps of 2004 - proud to be your copying solution. (Just kidding, that's wrong.)
1. How many electrons make up a charge of -30.0 mC
Since electrons have charges of –1.6E-19 C all we need to do is divide the
given charge by the electron charge to give us the number of electrons. Also,
be careful with the whole mili-coulombs thing.
-30 mC
/ 1.602E-19 C = 1.88 E14 electrons
(Table of
contents)
3. Two charged balls are 20.0 cm they are moved, and the
force on each of them is found to have tripled. How far apart are they
now?
Solving this problem is nice, because in this case while we
use the formula F = kq1q2/r2
we can ignore both charges and the variables F
and k. Since the resulting force is tripled, we know that the radius of the
new situation will be 1/3 of the original value of r2. To start this problem,
we need to set two equations equal to one another. This works because but
cutting the original value of r2 by 1/3, the two equations will be equal and
we can then solve for r in the new situation.
F = kq1q2/r2
kq1q2/r2 = kq1q2/r2
Remove unnecessary variables and set equations equal by multiplying
r2 by 1/3 in equation 1.
1 / ((1/3)* 202) = 1 / r2
(1/3) * (202) = r2
r = .012 m or 11.5 cm
(Table of contents)
5. What is the magnitude of the electric force of
attraction between an iron nucleus (q=+26e) and its innermost electron if the
distance between them is 1.5 x 10-12 m?
This is a straight up F = kq1q2/r2
problem from the hood.
It’s not too bad, the only trick here is the nucleus charge and to solve that
problem we simply multiply the first charge by +26 e. Plug in the values you
must, young Jedi.
F = kq1q2/r2
F = (8.99E9) * (26 * 1.602E-19 * 1.602E-19) /
(1.5E-12)2
F = .0027 N or 2.7E-3 N
(Table of contents)
7. What is the magnitude of the force a +15 - mC
charge exerts on a +3.0-mili coulombs charge 40 cm away? (1 mC=10-6
c, 1 mC=10-3c.)?
Questions like these are ones you cross your fingers for on
the test. Watch out for the whole mili- and mico- coulomb thing and remember
that two positive charges repel. Other than that you can pound this question
out with speed.
F = kq1q2/r2
F = (8.99E9) * (15E-6) * (3E-3) / (.4)2
F = 2.5E3 N
(Table of contents)
9. Imagine space invaders could deposit extra electrons in
equal amounts on the earth and now your car, which has mass of 1050 kg. note
that the rubber tires would provide some insulation. How much charge Q would
need to be placed on your car (same amount on earth) in order to levitate it
(overcome gravity) (hint : assume that earth charge is spread uniformly so it
acts as if it were located at the earth's center, and then the separation
distance is the radius of the earth.)?
Ok, seriously man. The author had a little too much time on
his hands to write this problem. Buts it’s assigned so lets get to
it.
Alright, so the first step is to figure out exactly how much force is
required to move your car. Using gravity as the acceleration to counteract,
remember these guys are levitating your car, we can use F = ma.
F = (1050 kg) (9.8 ms-2) = 10,290 N
Now, your car is on the surface of the earth, so the center to center
distance is the radius of the earth essentially, or 6.38 x 106
m. Setting the coulombic repulsion equal to the force of gravity on the
car we have:
10,290 N = kq1q2/r2
Now, since the two charges must be the same (read the problem), this
reduces to:
10,290 N = kq2/r2
10,290 N = (8.99 x 109 Nm2/C2)q2/(6.38x106m)2
q = 6825.7 C = 6.8e3 C
(Table of contents)
11. Particles of charge +70, +48, and +80 mC
are placed in a line (fig. 16-37) the center one is 0.35m from each of the
others. Calculate the net force on each charge due to the other
two.

First of all, you should have already sketched a diagram of
the figure because it makes things much, much easier. This problem really
isn’t that difficult, because we don’t have to deal with angles and instead
it is
just plain tedious. Solving this requires you to calculate both forces exerted
on each particle, determining whether that force is either attractive (like
me) or repulsive (like my stupid jokes). I will show how to use all the
necessary calculations for the +70 charge and after that, only the calculated
values.
(a) The force on the +70E-6:
Using F =
KQ1Q2/r2
+70 and +48:
F = kq1q2/r2
=
(8.99E9)(70E-6)(48E-6) / (.35)2 = 246.6 N (left - the 48 repels the
70)
+70 and –80:
F = kq1q2/r2
=
(8.99E9)(70E-6)(-80E-6) / (.7)2 = 102.7 N (right - attracted)
Then, just do a little net force action:
102.7 (right) - 246.6 (left) = -144 N
(left)
(b) The force on the middle one (The 48E-6 C)
Using F =
KQ1Q2/r2
+48 and +70 :
F = kq1q2/r2
= (8.99E9)(48E-6)(70E-6) / (.35)2 = 246.6 N (right - the 70 repels
the 48)
+48 and –80:
F = kq1q2/r2
= (8.99E9)(48E-6)(80E-6) / (.35)2 = 281.8 N (right - attracted)
Then, just do a little net force action:
246.6 N (right) + 281.8 N (right) = 528 N (right)
(c) The force on the right one (The -80E-6 C)
Using F =
KQ1Q2/r2
-80 and +48 :
F = kq1q2/r2
= (8.99E9)(80E-6)(48E-6) / (.35)2 = 281.8 N (left - attracted
-80 and +70:
F = kq1q2/r2
= (8.99E9)(80E-6)(70E-6) / (.70)2 = 102.7 N (left - attracted)
Then, just do a little net force action:
281.8 N (left) + 102.7 N (left) = 385 N (left)
(Table of contents)
12. Three positive particles of charge 11.0 mC
are located at the corners of an equilateral triangle of side 15.0 cm (Fig.
16-38). Calculate the magnitude and direction of the net force on each
particle.
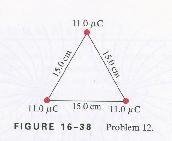
This problem seems hard because it seems like we’re going to
end up finding three different answers and plus, they’re not in a straight
line. However, all we need to do is calculate the magnitude and net force on
one particle because we are dealing with an equilateral triangle. To solve the
problem, we need to find the force one particle exerts on the
other.
F = kq1q2/r2 =
(8.99E9)(11E-6)2 / (.15)2 = 48.35 N
Now, because this is an equilateral triangle, we can assume
the angle that each particle is exerting on the other is 60o. Since the x-axis
displacement of each particle is the opposite of the other, they cancel one
another out and all we need to know is the y-axis displacement. To find it we
use good old Mr. Sine.
(48.35)(sin 60) = 41.87 * 2 (remember there are two different
particles acting on each) =
83.7 N (away from the
center)
(Table of contents)
13. A charge of 6.00 mC
is placed at each corner of a square 1.00 m on a side. Determine the
magnitude and direction of the force on each charge.
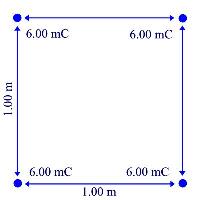
Make sure you make a diagram and draw arrows as to where the
force is going. Use F = kq1q2/r2
and calculate the magnitude and impact each (meaning all 3) charge has
on the other.
First find the force of the two particles that are not on a
diagonal. Since each particle produces and equal force, the charge will be
propelled diagonally, at an angle of 45 degrees.
F = kq1q2/r2 = (8.99E9)(6E-3)2
/ (1)2 = 323640 N
3236402 +3236402 = c2
c = 457696 N
Now, we solve for the third charge on the diagonal.
F = kq1q2/r2 =
(8.99E9)(6E-3)2 / 2
F = 161820 N
Now just add the two and the answer is yours.
F = 161820 + 457696 = 619516 N = 6.2 E5 N
(Table of contents)
15. Compare the electric force holding the electron in
orbit around the proton nucleus of the hydrogen atom, with the gravitational
force between the same electron and proton. What is the ratio of the these
two forces?
Solving this require us to use F = kq1q2/r2
to calculate the electric force
holding the electron in addition to the gravitational force between the two.
After calculating each, to find the ratio we simply divide the electric force
by the gravitational. Use the proton and electron’s charge for q1
and q2, the radius is diameter of a hydrogen atom divided by
two.
Electric Force: F = kq1q2/r2
=
(8.99E9)(-1.602E-19)(1.602E-19) / (.53E-10)2 =
8.2E-8 N
Gravitational Force: F =
Gm1m2/r2 =
(6.67e-11)(1.673e-27)(9.11e-31) / (.53e-10)2 =
3.6E-47 N
Divide and Conquer: 8.2E-8 / 3.6E-47 = 2.3E39 N ratio
Electric/Gravitational
(Table of contents)
19. A + 5.7 mC
and a - 3.5 mC
charge are placed 25 cm apart. Where can a third charge be placed so that
it experiences no net force?
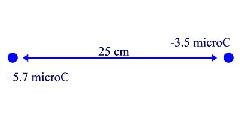
So we're trying to find r. We want the Forces to be equal, so:
kq1q2/r2 = kq1q2/r2
Q1 is the "third charge," so we can just cancel it out here, as
well as the K. So then we're left with:
(3.5mC)/r2 = (5.7mC)/(r+.25)2
Square root top and bottom on both sides...
(3.5mC)^(1/2)/r
= (5.7mC)^(1/2)/(r+.25)
((3.5mC)^(1/2))r
+ ((3.5mC)^(1/2))(.25)
= ((5.7mC)^(1/2))r
Solving for r, we get:
r = .91 m beyond the negative charge
(Table of contents)
21. What is the magnitude and direction of the
acceleration experienced by an electron in and electric field of 600 N/C?
How does the direction of the acceleration depend on the direction of the field
at that point? How does the direction of the acceleration depend on the
electron's velocity at that point?
First, looking at the given information, we know we can find Force using E
= F/q. From there, you can easily find the acceleration using F = ma.
Given info:
E = 600 N/C
q = 1.602e-19
E = F/q
600 N/C = F/(1.602e-19)
F = 9.612e-17 N
F = ma
9.612e-17 N = (9.11e-31)a
a = 1.055e14 m/s/s
Because it's an electron, it has a negative charge. This means
that the electron should always accelerate in the opposite direction of the E.
Field. This is why the direction of acceleration depends on the direction of
the E. Field.
(Table of contents)
23. A proton is released in a uniform electric field, and
it experiences an electric force of 3.2 x 10-14 N toward the
south. What are the magnitude and direction of the magnetic field?
Given Info:
F = 3.2e-14
q = 1.602e-19
E = F/q
E = 3.2e-14/1.602e-19
E = 1.997e5 N/C South
Because it is a proton (positive charge), it will always
travel with the magnetic field (away from the source is how I
think of it), and vice versa. So in this case, the magnetic field is in the
same direction as the force on the proton.
(Table of contents)
25. What is the magnitude and direction of the electric
field 30.0 cm directly above a 33.0 x 10-6 C charge?
Now, we're into point charges. In the info given, we have a radius
(distance between charge and point charge), as well as 1 Charge (33e-6 C).
E = kq/r2
E = (8.99e9)(33e-6)/(.3)2
E = 3.29e6 Up
Because this charge is positive, the electric field is always
away from the charge. If the point is directly above the
charge, then the electric field will travel out to the point, and past it...
up.
(Table of contents)
27. An electron is released from rest in a uniform
electric field and accelerates to the north at a rate of 125m/s2.
What is the magnitude and direction of the electric field?
Given Info:
a = 125 m/s/s
q = 1.602e-19
In order to solve for E with these givens, we have to use both E = F/q and
F = ma. Because you can substitute ma for F in the first equation:
E = F/q = ma/q
E = (9.11e-31)(125)/(1.602e-19)
E = 7.12e-10 south
Electrons always travel against the electric field magnitude.
Since the electron is traveling north, the electric field must be
south.
(Table of contents)
30. Use Coulomb's law to determine the magnitude and
direction of the electric field at points A and B in Fig. 16-41 due to the two
positive charges (Q = 9.0mC)
shown. Is your result consistent with Fig. 16-29b?
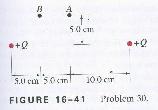
Vector Component Time
We'll solve for A first:
Notice the right triangles that you can create between point A
and the Q's.First thing you'll want to do is solve for the hypotenuse on one
of the sides. I chose the side on the right (it doesn't matter).
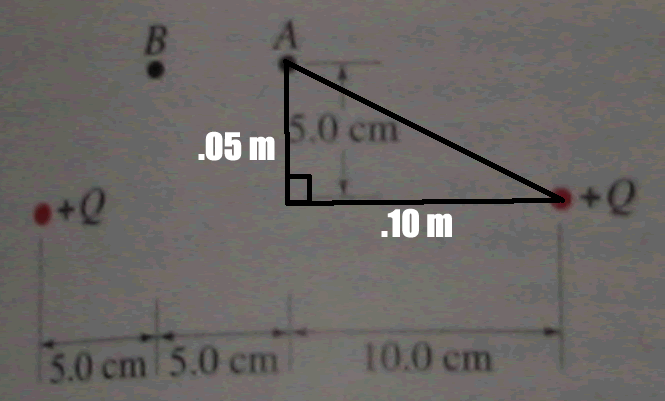
A2 + B2 = C2
52 + 102 = C2
C = .0125^(1/2)
The hypotenuse, then, is the distance between A and Q. a.k.a.
the radius, r. Since we already know K (a constant, 8.99e9) and Q is given
(9mC)
we can plug this into our equation for Electric Field:
E = kq/r2
E = (8.99e9)(9mC)/(.0125)
E = 6472800 N/C
Notice that .0125^(1/2) squared is just .0125...
Now that we have the Electric Field, we have to break it down
into components. First solve for the angle:
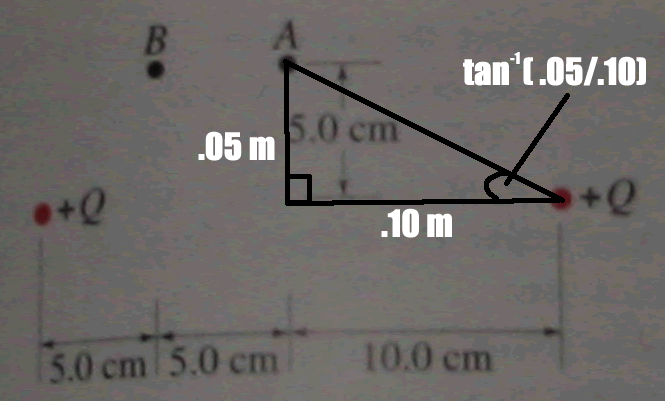
Angle is approximately 26.6 degrees. Now use that to find your
components.
sin(26.6)*(6472800) = Magnitude Up
cos(26.6)*(6472800) = Magnitude Left
Since the magnitude left will eventually cancel out with the magnitude
coming from the Charge on the other side of A, you can ignore that number. And
since essentially you'd be doing the same math over again, because its the
exact same distance and angle away, the Charge on the left side will yield the
same magnitude up. So at this point you can just multiply by two to get the
answer:
E = 5.8e8 N/C Up
For B:
I'll be brief with this one. Form your triangles again with B, and this
time you'll have to solve for the magnitude from both Charges. Follow the same
steps from part A (Hypotenuse, Solve for E, Break down to components, and Add
the components).
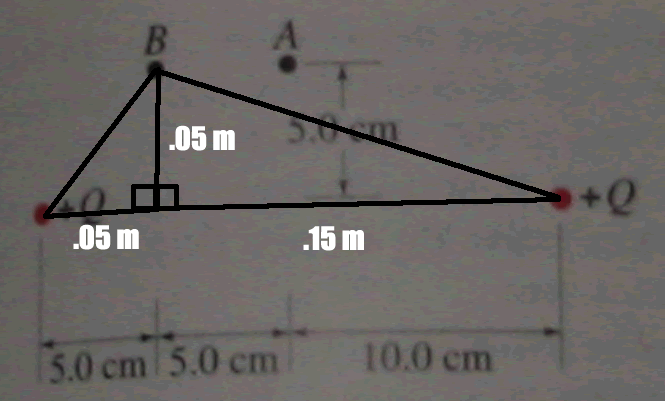
For the right side:
r = .025^(1/2)
E = (8.99e9)(9mC)/(.025)
E = 3236400 N/C
Angle = 18.4 degrees
sin(18.4)*3236400 = 1023439.54 N/C up
cos(18.4)*3235400 = 3070318 N/C left
For the left side
r = .005^(1/2)
E = (8.99e9)(9mC)/(.005)
E = 16182000 N/C
Angle = 45 degrees
sin(45)*16182000 = 11442401 N/C up
sin(45)*16182000 = 11442401 N/C right
1023439 + 11442401 = 12465840 N/C up
11442401 - 3070318 = 8372083 N/C right
(124658402 + 83720832)^(1/2) = 1.5e7 N/C 56 degrees
above horiz.
(Table of contents)
31. Calculate the electric field at the center of a square
60 cm on a side if one corner is occupied by a + 45.0-mC
charge and the other three are occupied by - 31.0-mC
charges?
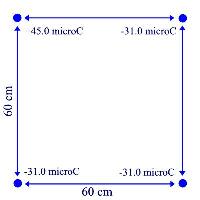
Since the Charges in the upper right and bottom left actually
cancel each other out, we can just focus on the positive charge and the
negative charge opposite of it diagonally. Ignore the fact that the negative
charges are in fact "Negative", that will only come in handy later when you
figure the direction of the magnitude.
r = .18^(1/2)
E = kq/r2
E = (8.99e9)(45mC)/(.18)
= 2247500 N/C 45 degrees below horiz
E = (8.99e9)(31mC)/(.18)
= 1548278 N/C 45 degrees below horiz
Since the Charge in the bottom left is negative, it is
actually pulling instead of pushing that point. Since the push of the positive
charge and the pull of the negative charge are in the exact same direction, we
just add em:
2247500 + 1548278 = 3.8e6 N/C 45 degrees below
horiz.
(Table of contents)
45. A water droplet of radius 0.018 mm remains stationary
in the air. If the electric field of the Earth is 150 N/C, how many excess
electron charges must the water droplet have?
Info Given:
Radius of the droplet: .000018 m
E = 150 N/C
Since there is no equation that can relate these two, we'll have to first
use the radius to find mass of the droplet.
m = d(4/3)pr3
d = (density) given = 1000
m = (1000)(4/3)(p)(.000018)3
m = 2.4e-11
Now that we have enough variables, we can use an equation to relate E
with m and g. Eq is the electric force, mg is the force of gravity.
Eq = mg
(150)(q) = (2.4e-11)(-9.8)
q = 1.6e-12
To find the number of electrons, we just divide by the
electron charge, 1.602e-19.
Number of extra electrons = 1.6e-12/1.602e-19 = 9.9e6 = 1.0e7
(Table of contents)
51. An electron with speed v0 = 1.5
X10-6 m/s is traveling parallel to an electric field (v0
][ E) of magnitude E = 7.7 X 103 N/C. (a) How far will it
travel before it stops? (b) How much time will elapse before it returns to
its starting point?
a)
Given Info:
E = 7.7e3 N/C
q = 1.602e-19
m = 9.11e-31
F = ma = Eq
a = Eq/m
a = (7.7e3)(-1.602e-19)/(9.11e-31) = -1.35e15
ms-2
After finding a, we now have enough (3) variables to simply
use SUVAT.
SUVAT
u = 1.5e-6 m/s
v = 0
a = -1.35e15 ms-2
v2 = u2 + 2as
(0) = (1.5e-6)2 + 2(-1.35e15)(S)
8.3e-4 m = S
b)
To solve for time, again we use SUVAT.
u = 1.5e-6
v = 0
a = -1.35e15 ms-2
v = u +at
0 = 1.5e-6 + (-1.35e15)(t)
t = 1.11e-9
To find the time it takes to fall to its original position,
we simply multiply by 2. (Similar to a rocket going up and down again... it
takes twice the time of going up).
t = (1.11e-9)*(2) = 2.22e-9 (nanoseconds)
(Table of contents)





