3. Sketch a PV diagram of the following process: 2.0 L of ideal gas at atmospheric pressure are cooled at constant pressure to a volume of 1.0 L, and then expanded isothermally back to 2.0 L, whereupon the pressure is increased at constant volume until the original pressure is reached.

(Table of contents)

First of all, draw your axis and label all known values on the graph. Next you start sketching the graph starting at the point 2 L , 1 atm , now all you do is follow the process, it is cooled at a constant pressure but in volume changes since it's temperature changes. Once you've drawn the first line you must expand it isothermally back to 2.0 L which looks like a diagonal line, once that is done all you have to do is return it to it's original pressure.

5. (II) One liter of air is cooled at constant pressure until its volume is halved, and then it is allowed to expand isothermally back to its original volume. Draw the process on a PV diagram.

(Table of contents)

This one is very similar to the previous problem, first draw your graph axis then beginning at 1 L you draw in constant pressure but split it's volume then you expand it isothermally back to it's original volume but in the end it has a different pressure that it half it's original pressure.

7. (II) In an engine, an almost ideal gas is compressed adiabatically to half its volume. In doing so, 1350 J of work is done on the gas. (A) How much heat flows into or out of the gas? (B) What is the change in internal energy of the gas? (C) Does its temperature rise or fall?

(Table of contents)

A) first of all we know that in an adiabatic compression or expansion no heat flows into or out of the gas, so naturally we know that the answer is 0 since no heat flows.

B) to compress the gas it takes 1350 J of energy, since energy is conserved we know that no other form of energy affects the gas except the energy that we administer, so the change in internal energy of the gas is +1350 J.

C) in an adiabatic compression temperature rises (energy is put in but no heat flows out so it must go up)

the following two-step process. Heat is allowed to flow out of an ideal gas at constant volume so that its pressure drops from 2.2 atm to 1.4 atm. Then the gas expands at constant pressure, from a volume of 6.8 L to 9.3 L, where the temperature reaches it's original value. See Fig. 15-27. Calculate (A) the total work done by the gas in the process, (B) the change in internal energy of the gas in the process, and (C) the total heat flow into or out of the gas.

(Table of contents)

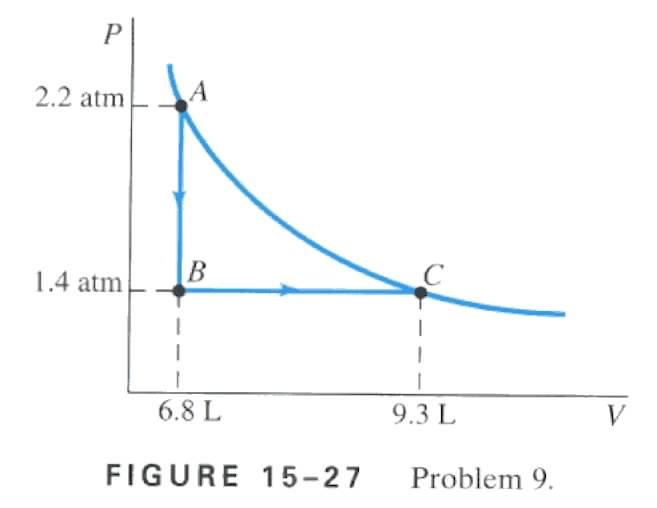
A) using figure 15-27 and the formula W = P DV are the keys to solving this problem, with both of those in mind it is easy to see where to plug in the numbers W = (1.4 x 10⁵)(9.3 x 10^-3 - 6.8 x 10^-3) , W = 350 J

B) Since the temperature at the beginning and at the end of the process are the same, there is no change in internal energy.

C) Since there is no change in internal energy DU = 0 , and using the first law of thermodynamics we come across this, DU = Q - W , then Q = W since DU = 0 , so since W = 350 J then Q must equal 350 J into the gas.

11. (II) When a gas is taken from a to c along the curved path in Fig. 15-29, the work done by the gas is W= -35 J and the heat added to the gas is Q= -63 J. (A) What is Q for the path abc? (B) If Pc = ½ Pb , what is W for the path cda? (C) What is Q for the path cda? (D) What is Ua - Uc ? (E) If Ud - Uc = 5 J, what is Q for the path da?

(Table of contents)

A) ITS BEEN TOO LONG..... FORGOT HOW TO DO

B)

C)

D)

E)

17. (I) A heat engine produces 8200 J of heat while performing 3200 J of useful work. What is the efficiency of this engine?

(Table of contents)

First of all we know that Efficiency = (Q₁ - Q₂)/ Q₁ where Q₁ = total work output and Q₂ = work wasted, so with that information you pretty much just plug the numbers in with Q₁ = 8200+3200 and Q₂ = 8200 , Efficiency = 3200/11400 and that equals .2807 which equals 28% efficiency.

(Table of contents)

With Efficiency = (Q₁ - Q₂)/ Q₁ , the rest of the problem is simple the only thing to remember is that the formula is in Kelvin's and they give you Celsius, so the rest is simple efficiency = ((580+273)-(320+273))/(580+273), which comes out to equal .3048 which equals 30%.

21. (II) A nuclear power plant operates at 75 percent of its maximum theoretical (Carnot) efficiency between temperatures of 600 C and 350 C. If the plant produces the electric energy at the rate of 1.3 GW, how much exhaust heat is discharged per hour?

(Table of contents)

Lets start off with the some formulas Q_L/ Q_H = 1 - E , so to solve for Q_L we need to find Q_H and the correct efficiency , so we will solve for the efficiency which is equal to E = (Q₁ - Q₂ )/ Q₁ , E = ((600+273)-(350+273))/ (600+273) , E = .286 but that is not the correct efficiency because it is running at 75% the ideal carnot efficiency so (.286)(.75) = .21478 , now with the correct efficiency we can now solve for Q_H using the formula E = W/ Q_H , so just insert the knowns .21478 = ((1.3 _E10)60)/Q_H , Q_H = 3.63 _E11 J finally we stick it back into the original formula Q_L/ Q_H = 1 - E , Q_L/ (3.63 _E11) = (1 - .21478) , Q_L = 2.85 _E11 J/s now just convert to hours (2.85 _E11)(60) = 1.71 _E13 J/h

(Table of contents)

To make the problem go easier we simplify the efficiency formula, E = (Q₁ - Q₂)/ Q₁ , EQ₁ = (Q₁ - Q₂) then E = 1 - (Q₂/ Q₂). With that taken care of we put some numbers in .39 = 1- ((350+273)/ Q₁) Q₁ = 1021.3, now with the total output solved for all we have to do is plug the new number back into the formula .50 = 1- (Q₂ /1021.3), Q₂ = 510.65 K now just convert back to Celsius 510.65-273 = 237.65 C.

31. (II) A heat pump is used to keep a house warm at 22 C. How much work is required of the pump to deliver 2800 J of heat into the house if the outdoor temperature is (A) 0 C? (B) -15 C? Assume ideal (Carnot) behavior.

(Table of contents)

A) the first thing we have to do is find the efficiency of this heat pump using the efficiency formula E = (Q₁ - Q₂)/ Q₁ , just plug in the correct numbers E= ((22+273)-(0+273))/(22+273), E = .0746% , now that we have the efficiency we can use the formula E = W/Q_H , plug in numbers...... .0746 = W/2800 , W = 208.88 J

B) this problem is exactly like the previous problem but with different numbers E = ((22+273)-(-15+273))/(22+273) , E = .1254 next formula... .1254 = W/2800 , W = 351.19 J

39.(II) 1.0 kg of water at 30 C is mixed with 1.0 kg of water at 60 C in a well-insulated container. Estimate the net change in entropy of the system?

(Table of contents)

First of all we know the entropy formula is equal to DS = Q/ T , second we need to solve for Q , Q = mcDt , and since the amounts are equal the end temperature of the solutions is equal to middle of 30C and 60C, Q = (1kg)(1.00kcal/kgK) (15C) , Q = 15 kcal , we also know that the total change in entropy is equal to DS = DS_H + DS_C , now with this information all we are missing is T , we need to solve for two T's the hot water T and the cold water T. So to solve for T you find the average temperature of each sample, ex. (60+45)/2 = 52.5 + 273 = 325.5 K for the hot and (45+30)/2 = 37.5+273 = 310.5 K for the cold. Now all you have to do is plug in numbers DS = - (15000cal/325.5K) + (15000cal/310.5K) , DS = + 2.23 cal/K