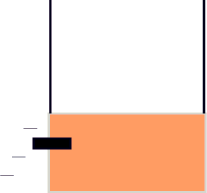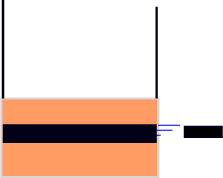Conservation of Momentum Questions: 0 | 1 | 2 | 3 | 4 |  Go up
 - by Chris Murray, 2002, 2004

0. A 125 g bullet going 516 m/s sticks into a 16.25 kg block of wood hanging from a very long string.  

A) What is the velocity of the block right after the collision?  

B) To what height does the block rise on the string?  

A bullet of the same mass makes the block rise to a height of .426 m.  

C) What was this bullet’s original velocity? 

Yet another 125 g bullet going 516 m/s goes right through the block, and is going 314 m/s after it goes through the block.  

D) What is the block’s velocity after it passes through, and 

  E) to what height does the block rise?

(Table of contents)

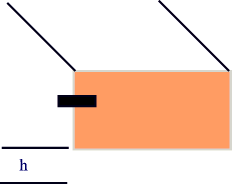
Here is a cartoon of what happens.  The impact of the bullet with the block conserves momentum, but a great deal of kinetic energy is lost to things like heat and work ripping through wood fibers.  The moving post-collision bullet and block combo swing on the string to some height, and in this, kinetic energy turns to potential.

 

Frame_1	Frame 2	Frame 3

A) What is the velocity of the block right after the collision?  
Right after the collision, the kinetic energy is not conserved, but the momentum is conserved as the earth has not taken away momentum yet by slowing the block.  (i.e. we are looking at the block and bullet combo right after the collision - if such time exists - before the block has moved)

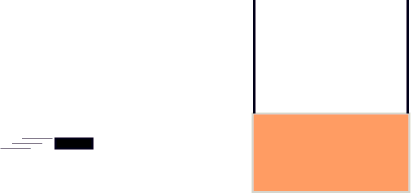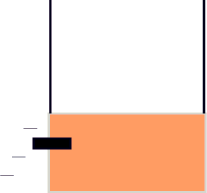(.125 kg)(516 m/s)     + 0	(.125 kg + 16.25 kg)v

v = 3.939 = 3.94 m/s
Back to problem 0


B) To what height does the block rise on the string?  
Here we can't use momentum as the block starts out moving, and in the end it has stopped moving (the earth presumably having carried away the momentum...).  We can use energy, as in the first frame, the block and bullet combo have kinetic energy, and in the end, there is gravitational potential.

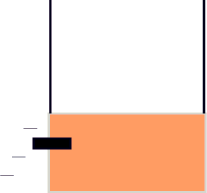1/2(.125 kg + 16.25 kg)(3.939)2           =	(.125 kg + 16.25 kg)(9.8 N/kg)h

h = .7916  = .792 m
Back to problem 0

C) A bullet of the same mass makes the block rise to a height of .426 m.  What was this bullet’s original velocity?   
This is the same thing as A and B, only all together.  Here is a cartoon of what happens.  The impact of the bullet with the block conserves momentum, but a great deal of kinetic energy is lost to things like heat and work ripping through wood fibers.  The moving post-collision bullet and block combo swing on the string to some height, and in this, kinetic energy turns to potential.  Since we are given the height, we have to start at the end, and work backwards:

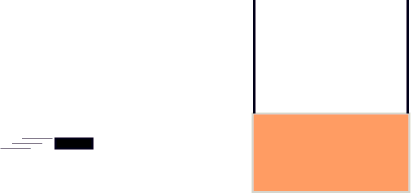
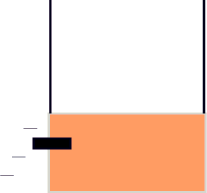Step_1	1/2(.125 kg + 16.25 kg)v2                 = v = 2.8896 m/s	(.125 kg + 16.25 kg)(9.8 N/kg)(.426 m)
(.125 kg)v     + 0                       =  v = 378.53 m/s	(.125 kg + 16.25 kg)(2.8896 m/s

v = 379 m/s
Back to problem 0

D) Yet another 125 g bullet going 516 m/s goes right through the block, and is going 314 m/s after it goes through the block.  What is the block’s velocity after it passes through?

E) Yet another 125 g bullet going 516 m/s goes right through the block, and is going 314 m/s after it goes through the block.  To what height does the block rise?

Here is a cartoon of what happens.  The bullet ripping through the block conserves momentum, but a great deal of kinetic energy is lost to things like heat and work ripping through the wood.  The moving  block swings on the string to some height, and in this, kinetic energy turns to potential.

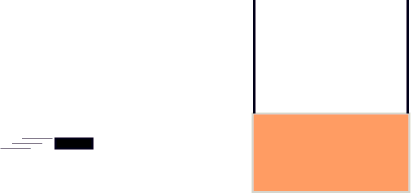
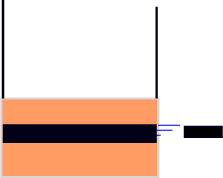(.125 kg)(516 m/s)     + 0	(16.25 kg)v + (.125 kg)(314 m/s) block's v = 1.5538 m/s
	1/2(16.25 kg)(1.5538 m/s)2      =	(16.25 kg)(9.8 N/kg)h h = .12318 m

From the first frame to the second, momentum is conserved, and from the second frame to the third, I will use kinetic turns to potential to solve for the height
Back to problem 0
(Table of contents)

1. 109 Kg Thor and his 5.26 Kg hammer are at rest on top of the first of two uncoupled frictionless 89.7 Kg carts that are next to each other. (Ok - its a physics word problem) Thor runs and jumps from one cart to the other and lands on it. (Still holding the hammer) He, the hammer, and the cart are going +1.56 m/s in the end.  
A) What must be the velocity of the other cart?  
B) What was Thor's velocity after he left the first cart, but before he landed on the second?  
C) With what velocity must he throw his hammer to give himself and the cart he lands on (Not the one he starts on) a velocity of 2.00 m/s?  
D) If instead of throwing the hammer in C), he were to jump from the second cart in such a way that he was not moving horizontally with respect to the ground, what would be the velocity of the second cart? 
(Table of contents)

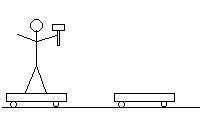
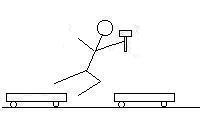
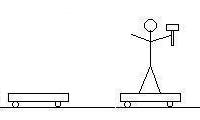
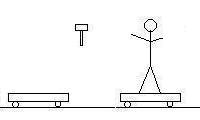
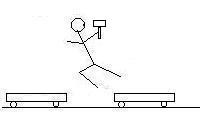
Here is a cartoon of what happens.  The total momentum of the system is zero in every frame, as everything is at rest in the first frame.

Frame 1	Frame 2	Frame 3	Ending part C	Ending part D

A) What must be the velocity of the other cart?  
Here you are comparing the first frame to the third.  The total momentum of the first frame is zero, and left to right, the third frame has an 89.7 kg cart going some velocity v, and 109 kg Thor holding a 5.26 kg hammer standing on the other 89.7 kg cart moving to the right at 1.56 m/s:

(Momentum is Zero)           0 =	(89.7 kg)v + (109 kg + 89.7 kg + 5.26kg)(+1.56 m/s)

v = -3.55 m/s
Back to problem 1


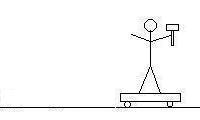
B) What was Thor's velocity after he left the first cart, but before he landed on the second? 
Here you are comparing the third frame to the second.  Since the first car does not change velocity from the second to the third frame, we can ignore it, and do the momentum of only Thor with hammer, and the second cart.  In the second frame, we have Thor moving to the right with an unknown velocity, and the second cart at rest, and the third frame has 109 kg Thor holding a 5.26 kg hammer standing on the other 89.7 kg cart moving to the right at 1.56 m/s:

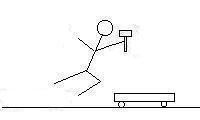(109 kg + 5.26 kg)v           =	(109 kg + 89.7 kg + 5.26kg)(+1.56 m/s)

v = 2.78 m/s
Back to problem 1

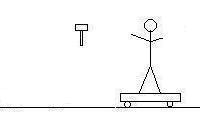
C) With what velocity must he throw his hammer to give himself and the cart he lands on (Not the one he starts on) a velocity of 2.00 m/s?  
In the before picture, I have109 kg Thor holding a 5.26 kg hammer standing on the second 89.7 kg cart moving to the right at 1.56 m/s, and after, we have the hammer moving to the left (most likely) and 109 kg Thor standing on the second 89.7 kg cart moving to the right at 2.00 m/s.  The first or leftmost cart is ignored as it does not interact with the other objects between frames.

(109 kg + 89.7 kg + 5.26kg)(+1.56 m/s) =	(5.26kg)v + (109 kg + 89.7 kg)(+2.00 m/s)

v = -15.1 m/s
Back to problem 1

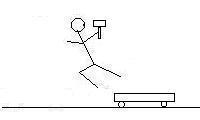
D) If instead of throwing the hammer in C), he were to jump from the second cart in such a way that he was not moving horizontally with respect to the ground, what would be the velocity of the second cart?   
In the before picture, I have 109 kg Thor holding a 5.26 kg hammer standing on the second 89.7 kg cart moving to the right at 1.56 m/s, and after, we have the hammer moving to the left (most likely) and 109 kg Thor standing on the second 89.7 kg cart moving to the right at 2.00 m/s. The first or leftmost cart is ignored as it does not interact with the other objects between frames.

(109 kg + 89.7 kg + 5.26kg)(+1.56 m/s) =	(109 kg + 5.26kg)(0 m/s) + (89.7 kg)v

v = +3.55 m/s
Which makes perfect sense, as the total momentum must be zero, and the first cart (not pictured) is still moving merrily along the frictionless surface to the left at -3.55 m/s, and the carts have the same mass.
Back to problem 1
(Table of contents)

2. Priscilla (65.4 Kg) is at rest on the first of two 82.0 Kg carts which are also at rest on a frictionless level surface. She jumps from the first cart to the second, and then to the ground.  Following this maneuver, the first cart has a velocity of -1.45 m/s, and the second a velocity of 2.26 m/s.
A. What was her velocity between the first and second cart?
B. What was her velocity between the second cart and the ground?
C. What would have been the velocity of her and the second cart if she had remained on the second cart instead of jumping off?
D. If her interaction with the first cart took 2.6 seconds, what force did she exert on it?
E. What would have been the velocity of the second cart if she was motionless after leaving it? 
(Table of contents)

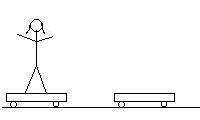
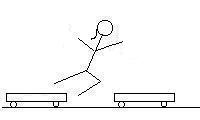
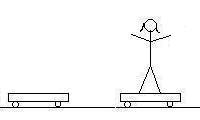
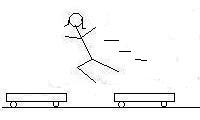
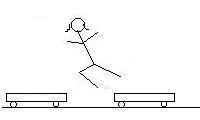
Here is a cartoon of what happens.  The total momentum of the system is zero in every frame, as everything is at rest in the first frame.

Frame 1	Frame 2	Frame 3	Frame 4	Director's Cut

A. What was her velocity between the first and second cart?
Compare the first frame to the second.  In the first frame the net momentum is zero as nothing is moving.  In the second frame, the first cart (leftmost one) is moving to the left  already at -1.45 m/s, and  Priscilla is moving presumably to the right with an unknown velocity:

(Momentum is Zero)           0 + 0     =	(82.0 kg)(-1.45 m/s) + (65.4 kg)v + 0

v = 1.82 m/s
Go back to problem 2

B. What was her velocity between the second cart and the ground?
Compare the first frame to the fourth.  In the first frame the net momentum is zero as nothing is moving. In the fourth frame, the leftmost cart is moving to the left with a velocity of -1.45 m/s, the right cart is moving to the right with a velocity of 2.26 m/s, and Priscilla is moving (presumably to the left) at some unknown velocity.

(Momentum is Zero)           0 + 0     =	(82.0 kg)(-1.45 m/s) + (65.4 kg)v + (82.0 kg)(+2.26 m/s)

v = -1.02 m/s
Go back to problem 2

C. What would have been the velocity of her and the second cart if she had remained on the second cart instead of jumping off?
Here you are comparing the first frame to the third.  The total momentum of the first frame is zero, and left to right, the third frame has an 82.0 kg cart going to the left at -1.45 m/s, and 65.4 kg Priscilla standing on an 82.0 kg cart moving to the right at some unknown velocity:

(Momentum is Zero)         0 + 0     =	(82.0 kg)(-1.45 m/s) + (65.4 kg + 82.0 kg)v

v = .807 m/s
Go back to problem 2

D. If her interaction with the first cart took 2.6 seconds, what force did she exert on it?
This problem is a horse of a different color.  (I just like that figure of speech - the mental imagery for me is great)
We know that
Impulse = Dp = FDt
and implicitly,  Dp = mDv
so ultimately, 
 FDt = mDv
Good so far, but what do we put into the equation?  Well, since we are trying to find the force she exerts on the first cart, all of this must have to do with the first cart.  The mass must be the cart's mass and the change in velocity must be the cart's change in velocity:
 F(2.6 s) = (82.0 kg)(-1.45 m/s)

F = -45.7 N which really should be -46 N with sig figs.
Go back to problem 2

E. What would have been the velocity of the second cart if she was motionless after leaving it?
Here you are comparing the first frame to the last.  The total momentum of the first frame is zero, and left to right, the last frame has an 82.0 kg cart going to the left at -1.45 m/s, and 65.4 kg Priscilla with a velocity of zero (she would have had to jump off the back of the cart) and an 82.0 kg cart moving to the right at some unknown velocity:

(Momentum is Zero)         0 + 0     =	(82.0 kg)(-1.45 m/s) + (65.4 kg)(0 m/s) + (82.0 kg)v

v = 1.45 m/s
This again makes perfect sense, as that is the opposite of the velocity the first cart has, and we know they have the same mass, and the total momentum is zero.
Go back to problem 2
(Table of contents)

3. Two 746 g blocks of wood are at rest on that by now familiar frictionless surface. A 123 g bullet is shot through the first and sticks in the second. Following this the first block is moving 12.5 m/s, and the second with the bullet stuck in it 34.6 m/s. Neither the bullet nor the blocks lose any pieces.
A. What was the bullet's velocity between the blocks? 
B. What was the bullet's velocity before it hit the first block?
C. Suppose the bullet's interaction with the first block had taken .0200 seconds. What force would it have exerted on the block?
D. If in actuality there had been a frictional force of about .50 N on the second block with the bullet stuck in it, over what time would it have been brought to rest?
E. Suppose the bullet had stuck in the first block, causing it to slide into and stick to the second block. What would have been the velocity of the bullet and the two blocks? 
(Table of contents)

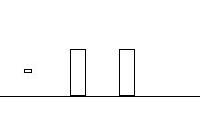
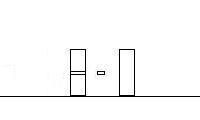
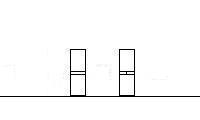
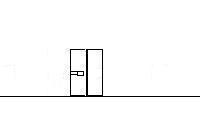
Here is the cartoon:

Frame 1	Frame 2	Frame 3	Ending part E

A. What was the bullet's velocity between the blocks? 
Compare the second frame to the third.  In the second frame, you have the first or leftmost block already moving at 12.5 m/s to the right, the bullet moving at some unknown velocity, and the second or right block not moving at all, but very nervous.  Shocked, really.  In the third frame, you have the scenario described in the problem, which is the first block is moving 12.5 m/s, and the second with the bullet stuck in it 34.6 m/s.

(.746 kg)(12.5 m/s) + (.123 kg)v + 0 =	(.746 kg)(12.5 m/s) + (.123 kg + .746)(34.6 m/s)

v = 244 m/s
Notice that we could have left the first block out of the picture altogether, as its velocity does not change from frame to frame, so we could solve this equation:
 (.123 kg)v   =  (.123 kg + .746)(34.6 m/s)
And gotten the same answer.
Go back to problem 3

B. What was the bullet's velocity before it hit the first block?
Compare the first frame to the third  In the first frame, the bullet is traveling at some unknown velocity, and the two blocks are at rest.  In the third frame, you have the scenario described in the problem, which is the first block is moving 12.5 m/s, and the second with the bullet stuck in it 34.6 m/s. 

(.123 kg)v + 0 + 0         =	(.746 kg)(12.5 m/s) + (.123 kg + .746)(34.6 m/s)

v = 320. m/s
Go back to problem 3

C. Suppose the bullet's interaction with the first block had taken .0200 seconds. What force would it have exerted on the block?
This problem marches to the beat of a different drummer.
We know that
Impulse = Dp = FDt
and implicitly,  Dp = mDv
so ultimately, 
 FDt = mDv
Good so far, but what do we put into the equation?  Well, since we are trying to find the force exerted on the first block, all of this must have to do with the first block.  The mass must be the block's mass and the change in velocity must be the block's change in velocity:
 FDt = mDv
F(.0200 s) = (.746 kg)(+12.5 m/s)

F = 466 N
Go back to problem 3

D. If in actuality there had been a frictional force of about .50 N on the second block with the bullet stuck in it, over what time would it have been brought to rest?
This problem is the raisin in the pudding.
We know that
Impulse = Dp = FDt
and implicitly,  Dp = mDv
so ultimately, 
 FDt = mDv
Applying this to the second bullet block system:
 (-.50 N)Dt = (.746 kg + .123 kg)(-34.6 m/s)
(the force and the change in velocity are both negative, as they are acting to the left, or are to the left)
Dt = 60. s
Go back to problem 3

E. Suppose the bullet had stuck in the first block, causing it to slide into and stick to the second block. What would have been the velocity of the bullet and the two blocks? 
Here you are comparing frame 3 to another possible ending.  In the third frame, you have the scenario described in the problem, which is the first block is moving 12.5 m/s, and the second with the bullet stuck in it 34.6 m/s.  In the other ending, you have both blocks, and the bullet traveling at some unknown velocity:

(.746 kg)(12.5 m/s) + (.123 kg + .746)(34.6 m/s)     =	(.123 kg + .746 kg + .746)v

v = 24.4 m/s
Go back to problem 3
(Table of contents)

4. A 45.00 kg exploding shell traveling at 684.0 m/s strikes the first of three 16.00 kg blocks of wood lined up in a row, initially at rest, and spaced a meter apart on a frictionless surface. The shell explodes upon impact with the first block, sending a 15.00 kg fragment backwards at 72.00 m/s. The remaining 30.00 kg of the shell penetrates the first and second blocks of wood, and sticks in the third. Following the collision the first block is moving in the original direction of the shell at 85.00 m/s, and the second, 320.00 m/s. Assume that the wood blocks lose no pieces. (hee hee)
A. What is the final velocity of the third block of wood with the 30.00 kg shell fragment in it?
B. What was the velocity of the 30.00 kg shell fragment between the first and second block?
C. What is the velocity of the 30.00 kg shell fragment between the second and third block?
(Table of contents)

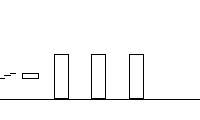
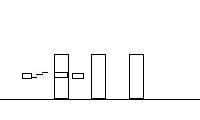
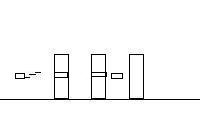
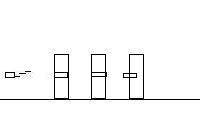
Here's the cartoon

Frame 1	Frame 2	Frame 3	Frame 4

A. What is the final velocity of the third block of wood with the 30.00 kg shell fragment in it?
Compare the first frame to the fourth.  In the first frame, the blocks are at rest, and the shell is moving at 684 m/s.  In the fourth frame, the shell fragment is moving to the left with a velocity of -72.00 m/s, the first block is moving at 85.00 m/s to the right, the second block is moving to the right at 320.0 m/s and the third block with the bullet stuck in it is moving at some unknown  velocity:

(45.00 kg)(684.0 m/s)     =	(15.00 kg)(-72.00 m/s) + (16.00 kg)(85.00 m/s) + (16.00 kg)(320.0 m/s) + (16.00 kg + 30.00 kg)v

v = 551.7 m/s
Go back to problem 4

B. What was the velocity of the 30.00 kg shell fragment between the first and second block?
Compare the first frame to the second.  In the first frame, the blocks are at rest, and the shell is moving at 684 m/s.  In the second frame, the shell fragment is moving to the left with a velocity of -72.00 m/s, the first block is moving at 85.00 m/s to the right, the the bullet is moving to the right with some unknown velocity, and the other two blocks are in angst, but not moving.

(45.00 kg)(684.0 m/s)       =	(15.00 kg)(-72.00 m/s) + (16.00 kg)(85.00 m/s) + (30.00 kg)v + 0 + 0

v = 1016.7 m/s
Go back to problem 4

C. What is the velocity of the 30.00 kg shell fragment between the second and third block?
Compare the first frame to the third.  In the first frame, the blocks are at rest, and the shell is moving at 684 m/s.  In the third frame, the shell fragment is moving to the left with a velocity of -72.00 m/s, the first block is moving at 85.00 m/s to the right, the second block is moving to the right at 320.0 m/s the bullet is moving to the right with an unknown velocity, and the third block is at rest.

(45.00 kg)(684.0 m/s)       =	(15.00 kg)(-72.00 m/s) + (16.00 kg)(85.00 m/s) + (16.00 kg)(320.0 m/s) + ( 30.00 kg)v

v = 846.0 m/s
Go back to problem 4
(Table of contents)