Conservation of Momentum: | 1 | 2 | 3 | 4 | 5 | 6 | 7 | Go up
 - by Bryan Holman, 2002

1. A 1200 Kg car going 13 m/s collides with a 4200 Kg truck at rest.  Their bumpers lock.  What is their speed afterwards?

So, the 1200 Kg car is going at 13 m/s before it collides with the 4200 Kg truck.  We know that p=mv, and that since there are two different cars, the formula would be mv_car + mv_truck = mv_both. So:

mv_car + mv_truck = mv_both

(1200 Kg)(13 m/s) + (4200 Kg)(0 m/s) = (1200 Kg + 4200 Kg)v

15600 = (5400 Kg)v

2.89 m/s = v
(Table of contents)

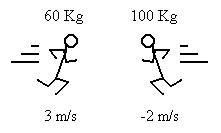
2. A 60 Kg person running 3 m/s collides head on with a 100 Kg person running -2 m/s (The other way)  What is their final velocity if they stick together?

First, I will call right positive, so here two people run into each other and end up going to the left.  We know that p=mv.  If you look at the first frame, the two people are running at each other (don’t ask me why), then collide in the second.  To find the momentum of the entire system, the formula would be: mv_{person a} + mv_{person b} = mv_both.  So: (The question states that they stick together but I didn’t want to make a picture of that because that would just look really weird)

mv_{person a} + mv_{person b} = mv_both

(60 Kg)(3 m/s) + (100 Kg)(-2 m/s) = (60 Kg + 100 Kg)v

-20 = (160 Kg)v

-.125 m/s = v (the answer is negative which means their final velocity is going to the left)
(Table of contents)

3. A 50 Kg ice skater at rest throws a 5 Kg shot put at a velocity of 3.5 m/s.  What is the recoil velocity of the skater?

This problem is very similar to the first two, except it starts out as a single object at rest, then goes to two separate objects moving at different speeds.  Still, p=mv as before, so the formula would be: mv_both = mv_{ice skater +} mv_{shot put}.  So: (If you couldn’t tell, those are ice skates on the bottom of the ice skater’s feet.  Don’t laugh at my drawings!)

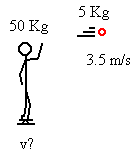mv_both = mv_{ice skater +} mv_{shot put}

(55 Kg)(0 m/s) = (50 Kg)v + (5 Kg)(3.5 m/s)

0 = (50 Kg)v + 17.5

-7.5 = (50 Kg)v

-.35 m/s = v (The negative implies that the ice skater is going to the left because I like right to be positive)
(Table of contents)

4. A 1200 Kg car going 15 m/s rear-ends with a 800 Kg car going 5 m/s in the same direction.  Their bumpers lock.  What is their speed afterwards?

This problem is exactly like question #1.  Therefore the same formula will be needed.  We know that p=mv, so mv_car + mv_truck = mv_both.

mv_car + mv_truck = mv_both

(1200 Kg)(15 m/s) + (800 Kg)(5 m/s) = (1200 +800)v

22000 = 2000v

v = 11 m/s
(Table of contents)

5. A 2000 Kg airplane going 45 m/s fires a 2 Kg shell forward at a speed of 1200 m/s.  What is the final velocity of the plane?  (Planes crashed because of this!)

The airplane and the shell are together at first, so because of the law of conservation of momentum the momentum of both the airplane and the shell when they are together will equal the momentum of both of them when they are separate.  P=mv, so the equation would be mv_both = mv_{plane +} mv_shell.

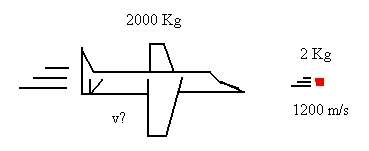mv_both = mv_{plane +} mv_shell

(2000 Kg + 2 Kg)(45 m/s) = (2000 Kg)v + (2 Kg)(1200 m/s)

90090 = 2000v + 2400

87690 = 2000v

v = 43.8 m/s
(Table of contents)

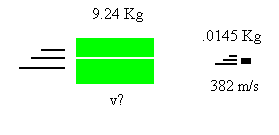
6. A 14.5 g bullet traveling 783 m/s horizontally strikes an 9.24 Kg block of wood at rest on a level frictionless table.  The bullet goes through the block, but is traveling only 382 m/s in the same direction after the collision.  What is the velocity of the block after the collision? (Assume the block loses no mass)

In this problem, the bullet travels through the block, and the block moves afterwards.  This is a before and after question.  We know that p=mv, and because momentum is conserved, we can figure out this problem.  The momentum of the bullet plus the block before will equal the momentum of both after: so the equation is mv_{bullet +} mv_block = mv_{bullet +} mv_block.  Remember that the block does not lose any mass.  Also remember to convert grams to kilograms.

mv_{bullet +} mv_block = mv_{bullet +} mv_block

(.0145 Kg)(783 m/s) + (9.24 Kg)(0 m/s) = (.0145 Kg)(382 m/s) + (9.24 Kg)v

11.3535 = 5.539 + 9.24v

5.8145 = 9.24v

v = .629 m/s
            (Table of contents)

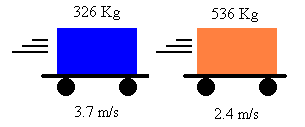
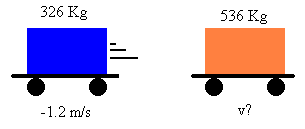
7. Bumper car A (326 Kg) with velocity 3.7 m/s collides with the rear of car B (536 Kg) which has a velocity of 2.4 m/s in the same direction.  After the collision, car A has a velocity of -1.2 m/s.  What is the velocity of car B after the collision.

This question is similar to the last one, a before and after problem.  The total momentum before the collision is the momentum of both cars, same with after.  So the total momentum before equals the total momentum after.  P=mv, so mv_{car A +} mv_{car B} = mv_{car A +} mv_{car B}.

mv_{car A +} mv_{car B} = mv_{car A +} mv_{car B}

(326 Kg)(3.7 m/s) + (536 Kg)(2.4 m/s) = (326 Kg)(-1.2 m/s) + (536 Kg)v

2492.6 = -391.2 + 536v

2883.8 = 536v

v = 5.4 m/s
(Table of contents)