2 Dimensional Motion: | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | Go up
 - by Eric Hess, 2002

1. Fred leaves the edge of a 12m tall cliff with a horizontal velocity of 4.8 m/s. What time is he in the air? How far from the base of the cliff does he land? What is his velocity upon impact with the water in terms of x and y components? 

Here's what you know, 

Horizontal

Vertical

Dx = ? vi = 4.8 m/s vf = 4.8 m/s a = 0 Dt = ?           Now we need to find Dx. We know Dt, since time is on both sides. We can use  vavg = Dx/Dt, solving for Dx.  Dx = vavg(Dt) = 4.8(1.565) = 7.5 m. So Fred landed 7.5 meters from the base of the cliff.  Now we're asked to find the horizontal and vertical components. Luckily, we've already found them. They told us that the horizontal velocity = 4.8 m/s, and we calculated the vertical to be -15.3 m/s, so the answer is 4.8 m/s x - 15.3 m/s y.

Dx = 12 m vi = 0 m/s vf = ? a = -9.8 m/s/s Dt = ? Solve for vf  vf2 = vi2 + 2a(Dx) = 0 + 2(-9.8)(12) vf2 = -235.2; vf  = -15.336 m/s Now solve for Dt using  vf = vi + a(Dt) -15.336 = 0 + (-9.8)(Dt) = -15.336/-9.8 =    1.565 sec. So Fred was in the air for 1.56 seconds.

(Table of contents)

2.  Rachel leaps from the edge of a cliff with a velocity of 3.3 m/s horizontally.  She hits the water 1.2 seconds later.  How far out does she land? What is her speed when she hits?  How high is the cliff? 

Here's what you know

Horizontal

Vertical

Dx = ? vi = 3.3 m/s vf = 3.3 m/s a = 0 Dt = 1.2 sec We can use the formula vavg = Dx/Dt to find the distance.  Dx = vavg(Dt) = 3.3(1.2) = 3.96 m.

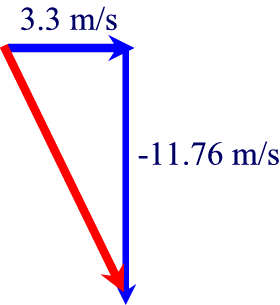
Dx = ? vi = 0 m/s vf = ? a = -9.8 m/s/s Dt = 1.2 sec     We know the horizontal velocity, now we need to find the vertical velocity. We can use vf = vi + a(Dt). vf = 0 + (-9.8)(1.2) = -11.76 m/s. So our vector map looks like this:                           And since speed is the hypotenuse, it equals:     3.3 m/s2 + (-11.76)2 = c2, so c = 12.2 m/s Finally, we need to find Dx, the height. Dx = 1/2(vi + vf)Dt = 1/2(0 + 11.76)1.2 = 7.1 m

(Table of contents)

3. A golf ball leaves the ground with an initial vertical velocity of 53 m/s and a horizontal velocity of 42 m/s.  a) Draw the initial velocity vector.  Find the initial speed. b) For what time is the ball in the air?  c) How far does it go in this time?

First, we are asked to draw the vector:

 

And now, we're supposed to find the speed. And speed is the hypotenuse. Since 42 m/s² + 53² = c², c = 67.6 m/s

Now, we need to set up a table to find the time, and horizontal distance:

Horizontal	Vertical
Dx = ? vi = 42 vf = 42 a = 0 Dt = ?       As the Stones put it, "Time is on both sides," so we know time = 10.8 horizontally also. Now we can use  vavg = Dx/Dt to find out the distance.  Dx = vavg(Dt) = 42(10.8) = 453.6 m = 454 m	Dx = ? vi = 53 m/s vf = -53 (what goes up, must come down) a = -9.8 m/s/s Dt = ? First, we need to find the time. We can use   vf = vi + a(Dt), -53 = 53 + (-9.8)Dt Dt = -106/-9.8 = 10.8 seconds

(Table of contents)

4. A rifle is fired at an angle 35^o above the horizontal at a speed of 720 m/s.  a) Draw a picture of the initial velocity vector.  b) What is the horizontal velocity?  c) What is the initial vertical velocity component? d) What time will the shell be in the air?  e) What distance will it go in that time?

First, lets draw the vector:

      

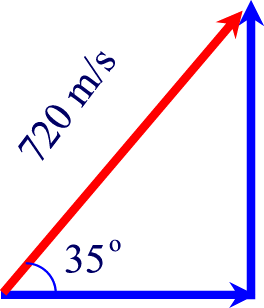
Now, they want us to find the horizontal velocity, which we can find using the cosine of the 35^o angle.

cos(35) = x/720,    x = cos(35)720 = 589.79 = 590 m/s horizontal velocity

Now, to find the vertical velocity, we can use the sine of the angle

sin(35) = x/720,    x = sin(35)720 = 412.98 = 413 m/s vertical velocity

Now we can use our table:

Horizontal	Vertical
Dx = ? vi = 590 vf = 590 a = 0 Dt = ?       And since time is on both sides, we can use Dx = vavg(Dt) to find the distance. Dx = 590(84.3) = 49,729 = 49,700 m that the bullet travelled.	Dx = ? vi = 412 vf = -412 a = -9.8 m/s/s Dt = ? To find time, we use: vf = vi + a(Dt), -413 = 413 + -9.8(Dt) Dt = -826/-9.8 = 84.3 seconds

(Table of contents)

5. A river has a current of 1.5 m/s, and a swimmer has a velocity of .89 m/s.  If they head straight across the river, what will be their speed (hypotenuse) with respect to the shore?  If the river is 45 m wide, how much time will it take them to cross?  How far downstream will they drift in that time? 

First, lets draw the vector:

    

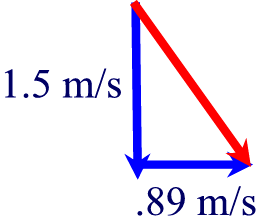
The speed would be the hypotenuse, or 1.5² + .89² = c², so c = 1.74 m/s.

So, our table looks like:

Horizontal	Vertical
Dx = 45 m  vavg = .89 m/s Dt = ? To find time, we can use vavg = Dx/Dt: Dt = Dx/vavg = 45/.89 = 50.56 m/s or 50.6 m/s	Dx = ? vavg = 1.5 m/s Dt = ?     The distance downstream that they'll drift is just the vertical distance. Time is on both sides, so again we can use vavg = Dx/Dt: Dx = vavg(Dt) = 1.5(50.56) = 75.8 m

(Table of contents)

6. A canoe heads straight across a river with a current of .80 m/s.  It takes the canoe 35 seconds to cross the 75 m wide river.  What is the speed of the canoe with respect to the water?  How far does the canoe drift downstream?  What is the speed of the canoe with respect to the shore? 

This is just like the last problem, but backwards. We need to fill in the table to draw the vector.

Horizontal	Vertical
Dx = 75 m vavg = ? Dt = 35 seconds First, they ask for the speed (velocity) of the canoe. Just use: vavg = Dx/Dt: = 75/35 = 2.14 m/s	Dx = ? vavg = .80 m/s Dt = 35 seconds     Then it asks for the vertical distance.                           Use vavg = Dx/Dt: Dx = vavg(Dt) = .80(35) = 28 m

Now we have all the information to draw the velocity vector:

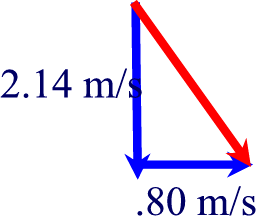
c² = 2.1429² + .80², c² = 2.29 m/s

(Table of contents)

7. Use the range and angle equations for this part: Angle = 67^o, Speed = 420 m/s, Range = ?

Here we can just use the equation for range.

range = (v²/g)sin(2q)

range = (420²/9.8)sin(2 x 67^o) = 12,948 m

(Table of contents)

8. Angle = 12o, Speed = 45 m/s, Range = ?

          Again, just use the range equation

range = (v²/g)sin(2q)

range = (45²/9.8)sin(2 x 12^o) = 84 m

(Table of contents)

9. Angle = 82o, Speed = 24 m/s, Range = ?

Again, just use the range equation

range = (v²/g)sin(2q)

range = (24²/9.8)sin(2 x 82^o) = 16.2 m

(Table of contents)

10. Speed = 34 m/s, Range = 62 m, Angle = ? 

Use the range equation, solving for the angle

q = (sin^-1(g(range))/v²)/2

q = (sin^-1(9.8(62))/34²)/2 = 15.9^o

(Table of contents)

11. Speed = 12 m/s, Range = 11 m, Angle = ?

Solving for the angle,

q = (sin^-1(g(range))/v²)/2

q = (sin^-1(9.8(11))/12²)/2 = 24.2^o

(Table of contents)

12. Speed = 24 m/s, Range = 62 m, Angle = ?

Solving for the angle,

q = (sin^-1(g(range))/v²)/2

q = (sin^-1(9.8(62))/24²)/2 = Can't take the sin of a number greater than 1, so the problem is impossible

(Table of contents)