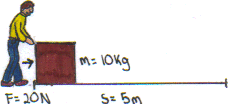 Time = 10 seconds
Time = 10 secondsHere, W=Fs, so W=(20)(5)=100J
| W | work | |
| P | Power | |
| KE | Kinetic Energy | |
| PE | Gravitational Potential Energy |
| Work: | W = Fs cos (q) | |
| Work in Lifting: | W = wh = mgh | |
| Power: | P = W/t = Fs cos (q)/t | |
| Kinetic Energy: | KE = 1/2 mv2 | |
| Gravitational Potential Energy: | W = wh = mgh |
Is what is accomplished by the action of a force when it makes an object move through a distance. It is represented by the equation: W=Fs; where F is the force and s is the displacement. Force, as you know, is in the units of Newtons (N) and displacement is in meters (m). So, Work is in Nm (Newton meters). Probably in all the problems you do in this class you will be using the units of Joules (J); where 1J= 1 Nm. In 2 identical situations where work is being done (where there is a force being applied to distance), the work is the same regardless of the time it takes to do it:
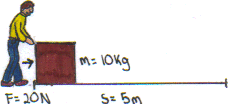 Time = 10 seconds
Time = 10 seconds
Here, W=Fs, so W=(20)(5)=100J
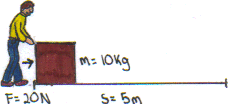 Time = 20 seconds
Time = 20 seconds
Here, the work still =100J. So, Work is not dependent upon time. (It's the Power that is dependent... go down for more).
When the Work is done parallel to the ground you use the simple equation W= Fs. However, sometimes the work is done at an angle. In this case, you use the equation W= Fs cos(. If you think about it, it is the same equation that you use even when an object is parallel to the ground, since the cos (0)= 1. (Zero since there is no angle). Here is an example of when to use the W= Fs cos
q
formula:
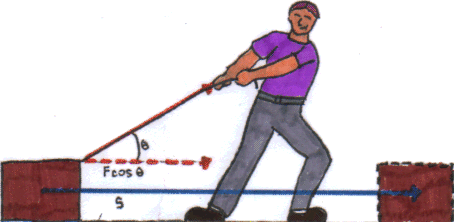
s=5m and F=20N just like in the previous problem, but this time
q
=60o
W=(20)(5)cos(60)= (100)(.5)=50N, instead of 100N
**Just as a note: A force can be exerted on an object and yet do no work. This happens if the displacement is zero. For instance, if you are at rest, even though you are holding a bag of groceries and are exerting force, since there has been no displacement, the work is still zero. So, for there to be work, the must be a force with a displacement occurring in the same direction.
Power is simply the rate at which work is done.
Power = Work / Time P = W/A
Since Work is in J and time is in seconds, P = J/s; 1 J/s= 1 W (Watt). Here is where the time at which a situation's work is done matters:
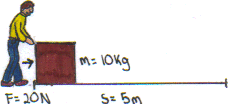 Time = 10 seconds
Time = 10 seconds
P= W/t. We calculated before that the W was 100N; the time is 10 sec; so P= (100)/(10)= 10W
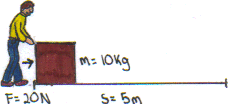 Time = 20 seconds
Time = 20 seconds
P=W/t; P= (100)/(20)= 5W
In identical situations, the faster you get the task done, the higher the power output.
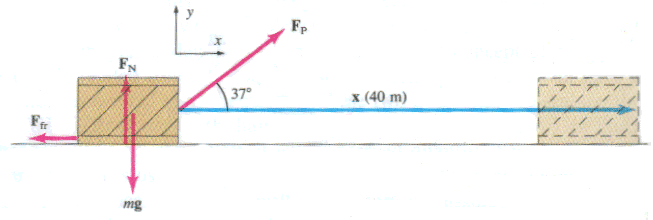
A 50-kg crate is pulled 40m along a horizontal floor by a constant force exerted by a person, Fp = 100N, which acts at a 37o angle. The floor is rough and exerts a friction force Ffr =50N. Determine the net work done on the crate.
** in this problem, s=x
OK, to do this I would calculate the 4 individual works that are done and add them together at the end. There are 4 forces here:
Wg = OJ
WN = OJ
This is because the q =90o... Cos(90o)=0
The work done by Fp is
Wp = Fpxcos( = (100N)(40m) cos 37o = 3200J
The work done by the friction force is
Wf = Ffrxcos (180) = (50N)(40m) (-1) = -2000J
**The angle is 180o because x and Ffr point in opposite directions. Since cos 180o = -1, we see that the force of friction does negative work on the crate. Finally, the net work is: Wnet = Wg + WN + Wp + Wf = 0 + 0 + 3200 - 2000 = 1200J
How far must a 200-kg pile driver fall if it is to be capable of doing 13,000J of work?
W=Fs
W=(m*a)s
W=13,000 m=200 a=9.8 (gravity) s=?
13,000= ((200)* (9.8))s
s= 6.63m
A 70-kg jogger runs up a long flight of stairs in 4.0s. The vertical height of the stairs is 4.5m. Estimate the jogger's power output in Watts.
The work is done against gravity, so the power P is
P= (m*g)/t ; m=70 g=9.8 s=4.5 t=4
= ((70)(9.8)(4.5))/4 =770W
| Work: W = Fs = Fs cos q | ||
| 144 J | 1.How much work does Fred do exerting 45 N to lift a box 3.2 m? W = Fs W = (45)(3.2) W = 144 J | |
| 7.5 m | 2.What distance will 90 J of energy slide a box against 12 N of frictional force? W = Fs 90 = (12)s 90s = 12 s = 90/12 s = 7.5 m | |
| 1.25 N | 3.Katherine moves a box 7.2 m doing 9 J of work. What is the frictional force? W = Fs 9 = F(7.2) F = 9/7.2 F = 1.25 N | |
| Work and weight: DEp = mg Dh | ||
| 4060 J | 4.How much work is needed to lift a 45-Kg box 9.2 m? DEp = mg Dh DEp = (45)(9.8)(9.2) DEp = 4057.2 DEp = 4060 J | |
| 102 Kg | 5.A pump does 4500 J of work in a minute. What mass of water can it pump to a height of 4.5 m in one minute? DEp = mg Dh 4500 = m(9.8)(4.5) m = 4500/(9.8)(4.5) m = 102 Kg | |
| 425 m | 6.A rifle cartridge contains 250 J of energy. How far can it launch its 60 gram slug into the air if it is shot straight up? DEp = mg Dh 250 = (60 g)(9.8)h 250 = (.06 Kg)(9.8)h 250 = (.588)h h = 250/.588 h = 425 m |
|
| Power:P = DW/ Dt | ||
| 60 W | 7.A motor can do 540 J of work in 9.0 seconds. What's its power output? P = DW/ Dt P = 540/9 P = 60 W |
|
| 18 s | 8.In what time can a 250 W motor do 4500 J of work? P = DW/ Dt 250 = 4500/ Dt Dt = 4500/250 Dt = 18 |
|
| 7500 J | 9.How much work does a 25 W motor do in 5 minutes? P = DW/ Dt 25 = DW/5 min 25 = DW/(5 min)(60 s/1 min) 25 = DW/300 DW = (25)(300) DW = 7500 J |
|
| Jambalaya: W = Fs, DEp = mg Dh, P = DW/ Dt | ||
| 35280 W | 10.What must be the power rating of a motor that can lift a 600 Kg load 30 meters in 5 seconds? DEp = mg Dh DEp = (600)(9.8)(30) DEp = 176400 DEp = DW P = DW/ Dt P = 176400/5 P = 35280 W |
|
| 188 W | 11.A sled dog drags a 240 Kg sled 50 m in 35 seconds when the coefficient of friction between the snow and the runners is .056.What is the power output of the dog? W = Fs, P = DW/ Dt, Ffr = mkFN, FN = mg Ffr = mkFN, FN = mg Ffr = (.056)(240)(9.8) Ffr = 131.712 W = Fs W = (131.712)(50) W = 6565.6 P = DW/ Dt P = 6585.6/35 P = 188 W |
|
| 2870 s | 12.Greg LeMond can put out 3/4 of a horsepower.(1 HP = 745.7 W).In what time can he climb a 2000 m mountain if he and his bike have a mass of 82 Kg? (Ignore Friction) DEp = mg Dh DEp = (82)(9.8)(2000) DEp = 1607200 J DEp = DW (3/4)(745.7) = 559.275 W P = DW/ Dt 560 = 1607200/ Dt Dt = 1607200/560 Dt = 2870 s |
|
| 900 N | 13.My van can only go about 25 m in one second on a level road at full power.(30 HP,1 HP = 745.7 W)What must be the force of friction opposing my van?(most of this is air friciton and drag) W = Fs, P = DW/ Dt P = (30)(745.7) = 22371 W P = DW/ Dt 22371 = DW/1 W = Fs 22371 = F(25) F = 900 N |
|
| 163 Kg | 14.A steam engine must drag logs across 45 m of level rock. If the coefficient of friction between the logs and the ground is .78, and the engine can put out 5 Horse power (1 HP = 745.7 W), what is the maximum mass of logs it can drag in 15 seconds? W = Fs, P = DW/ Dt, Ffr = mkFN, FN = mg P = (5)(745.7) = 3728.5 3728.5 = DW/15 DW = (3728.5)(15) DW = 55927.5 W = Fs 55927.5 = F(45) F = 55927.5/45 F = 1241.8 Ffr = mkFN, FN = mg 1241.8 = (.78)(9.8)(m) m = 163 kg |
|
| 4800 m | 15.A hiker can put out 250 W of power. If they have a mass of 72 Kg and are carrying a 43 Kg pack, what elevation gain can they expect to achieve in 6 hours of hiking? P = DW/ Dt DEp = mg Dh DEp = DW P = mg Dh/ Dt 250 = (72 + 43)(9.8)h/6 hr 250 = (115)(9.8)h/(6 hr)(60 min/1 hr)(60 s/1 min) 250 = (1127)h/21600 s 5400000 = 1127h h = 5.4 x 106/1127 h = 4791.48 h = 4800 m |