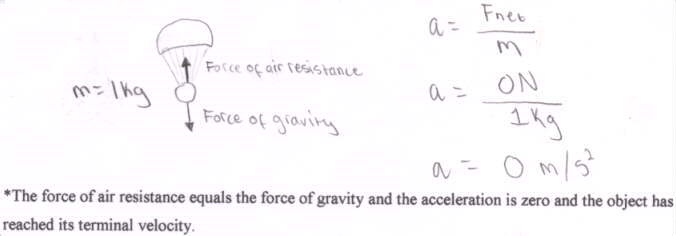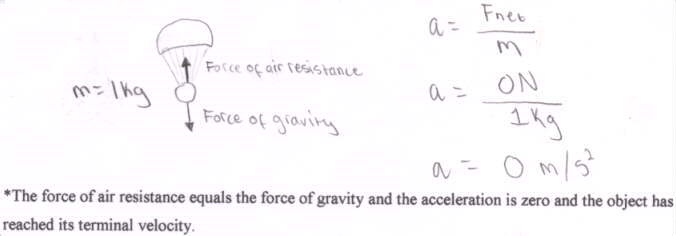EFFECTS OF DIFFERENT SIZE AND SHAPE PARACHUTES ON TERMINAL VELOCITY

Reina White & Ruth Hodgson

Research question: TOC

What is the relationship between Surface Area and Terminal Velocity?

Introduction: TOC

If you were to drop an object off a building, the speed of the object may not continually increase as it is going down. If the object falls far enough, it will reach a maximum velocity, called the terminal velocity, and will remain at that velocity the rest of the way down (Giancoli 30). Air resistance occurs because air molecules collide with the free-falling object and create an upward force against gravity (Jian Huang). To reach terminal velocity the air resistance and the force of gravity, or weight, must be balanced out and the acceleration of the object be equal to zero.

For example:

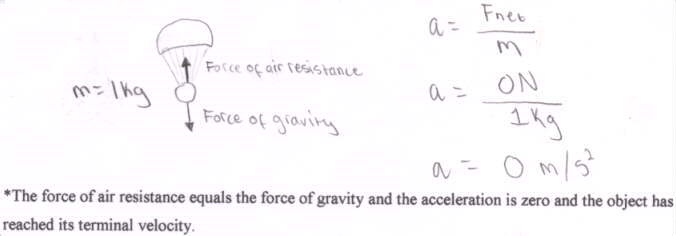
We know that weight affects the terminal velocity because it affects the force of gravity on the object. Another factor, the one we will be testing, is the amount of air that the object will be exposed to. The position in which the object falls changes the surface area and in turn changes the terminal velocity. If the object has a greater surface area it will have more room for air resistance to work on it. There will be a greater upward force and a smaller terminal velocity. If the object has a smaller surface area there will be less room for air to work on it and there will be less of an upward force and a greater terminal velocity. We learn from Jian Huang that the greater the object's surface area, the smaller the terminal velocity. But what is the relationship between surface area and terminal velocity? What kind of graph does it produce? Is it a linear relationship? We will be testing these factors with a parachute.

Hypothesis: TOC

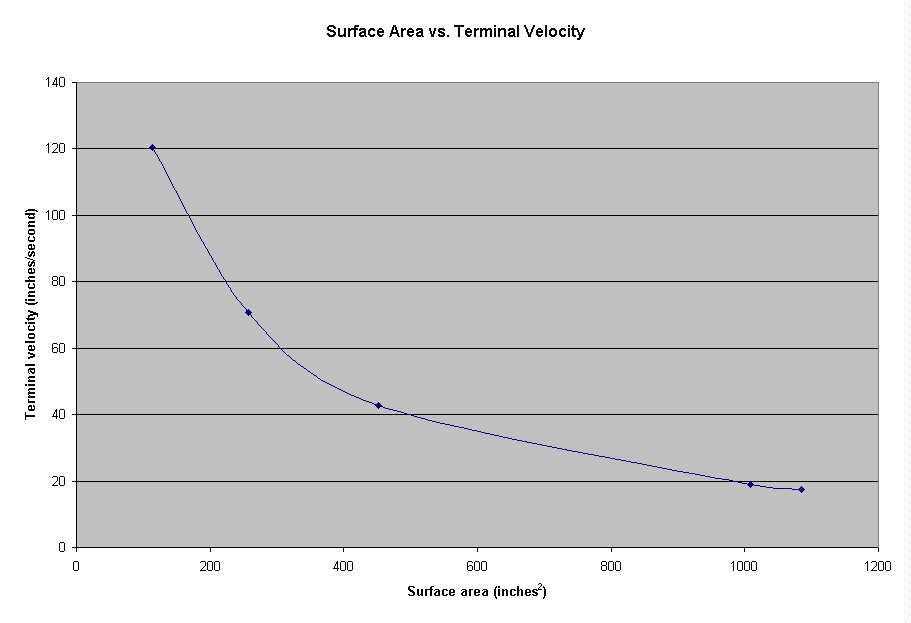
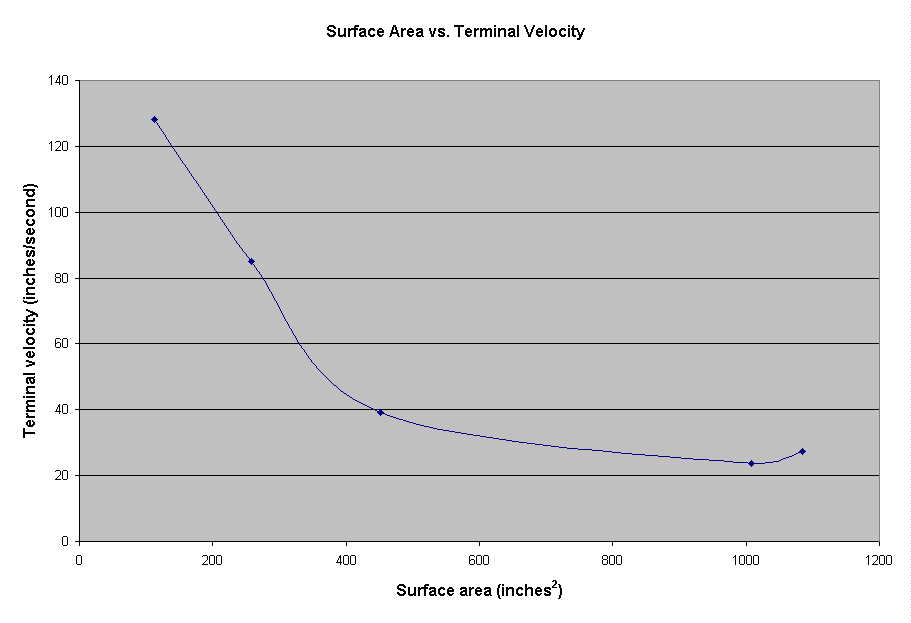
As the Surface Area of the parachute increases, the Terminal Velocity decreases in a curve-like relationship.

Materials: TOC

• * Parachute :
• ~string
• ~plastic bags
• ~bottles
• ~weights (ok, so they were pebbles)
• * Tape
• * Stop watch
• * Measuring tape
• * Rulers
• * Scale

Procedure: TOC

• 1) Make Parachutes: Using the plastic bags, string, bottles & tape we made 5 different shaped parachutes with different surface areas: Hexagon, Rectangle, Octagon, Triangle and a Circle. We then got out the scale and took their masses. Of course, they all weighed differently, so we out to her back yard and grabbed some pebbles and filled the bottles appropriately so that they all had approximately the same mass. We then measured the surface areas of the different parachutes (This was quite difficult and took some time considering both Reina & I did not know how to figure out the area of the Hexagon or Octagon!)
• 2) Drop Them: Using Reina's balcony, we suspended a tape measure from the top to the bottom, then taped it to the wall. Reina took all the parachutes to the top of the balcony while I figured out how to use the timer. Reina had to open the larger parachutes up before they dropped since the balcony was not high enough for the parachute to open by itself on time before they would hit the ground.
• 3) Get Data: Once Reina said go, I started the timer at the same instant Reina let the parachute drop. Reina & I both looked at the parachute going down and approximated where it looked like the parachute started going at a constant velocity and that's when I stopped the watch. Reina & I then had to compromise on the height that we each thought it went, and came up with a number around about the middle of our two estimations.

Data:TOC

Trial 1

Trial 2

Uncertainties... Lots! TOC

• ~Time: the time that we got was the time for my approximation of the terminal velocity. But, Reina and I had to approximate the distance (which is another uncertainty within itself) and when dividing distance by my time, the results are a little different.
• ~Estimating distance: this is an obvious uncertainty, but we couldn't think of any other way to do it.
• ~Opening the parachute: The fact that we had to open the bigger parachutes (the rectangle & the octagon) so they could reach their terminal velocity probably messed up the results somehow. This is probably why the results for the octagon on Trial 2 look out of place.
• ~Perhaps the temperature of the room had something to do with the amount of upward friction force that the parachute was subjected to. More moisture might mean more molecules to collide with and a higher upward force?
• ~Also, we found out that triangle parachutes like to twirl, or at least ours did! It made the triangle parachute move a lot instead of going straight down. This was NOT fun when we were trying to get our data. We were thinking of getting some fishing wire and stringing the parachutes down that. But we thought that somehow putting holes in the parachute would not be such a good idea. Also, it would cause an uncertainty with friction.

Conclusion: TOC

The fact that the parachutes were different shapes probably messed up our results also. We realized afterwards that if we really wanted to test the effect of surface area on terminal velocity we should have used the same shape parachute and changed the surface area so that it would have been the only variable. Or, if we just wanted to figure out the effects of shape on terminal velocity, we should have just kept the surface area constant. But, if we want to decide that the shape of the parachute doesn't matter all that much, then this experiment is pretty valid. It shows the higher the surface area, the lower the terminal velocity, and that this relationship is curve-like. This curve shows that at first, when the surface area is originally increasing, the terminal velocity is decreasing at a rapid rate. Then, later on when the surface area is much bigger, the terminal velocity is decreasing at a much slower rate. This is because the higher the surface area, the more room for air molecules to exert an upward force on the parachute, and therefore takes longer to equal the force of air friction. I think that if this graph were extended even further, somewhere down the line there would be some sort of limit occurring because even though the surface area can extend as far as it wants, there shouldn't be an object with a terminal velocity of zero.

Links: TOC

1. http://www.sciencejoywagon.com/physicszone/lesson/02forces/terminal/term1.htm -- An excellent clear and basic coverage on what terminal velocity actually is. I would recommend this as the first page to go to as an understanding of the basic concepts of terminal velocity.
2. http://hypertextbook.com/facts/JianHuang.shtml -- Although short, this site contains a good explanation of terminal velocity. Also includes an animation that clearly demonstrates terminal velocity.
3. http://www.engr.sc.edu/its/matt/Physics/theory.htm -- The theory behind terminal velocity. This site contains various ways to calculate the terminal velocity of an object falling in different mediums through the use of formulae.
4. http://www.indy.cc.ks.us/Science/phyeng/StudentProjects/PowerPoint/terminal/Terminal%20Velocity%20presentation_files/frame.htm -- This is a PowerPoint presentation dedicated to the explanantion of various aspects of terminal velocity. This includes terminal velocity vs mass, terminal velocity vs surface area, and terminal velocity vs different mediums.
5. http://www.processassociates.com/process/separate/termvel.htm -- A pretty cool calculator of a single rigid particle's terminal velocity. If you enter in the particle's diameter and density along with the density and viscosity of the surrounding fluid, it will calculate the terminal velocity of that particle.