Pursuing the Chaotic Dynamics of Nucleate Boiling .:. Go Up
Chris Murray
Tualatin High School
Jack Semura
Portland State
University
Table of contents:
Introduction
Method
Results and Discussion
Acknowledgements
Links
Abstract
At high rates of flow, dripping faucets display chaotic behavior. We investigated whether the bubbles leaving a nucleation site in boiling water exhibited the same kind of chaos. We gathered time series data for bubbles leaving a single nucleation site using a laser and photo-diode, and searched for strange attractors. Although we never saw a true attractor, some data suggested pre-chaotic behavior.
Introduction Table of Contents
When a leaky faucet drips at low rates, the dripping is periodic. The drips are separated by the same amount of time: (drip... drip... drip... drip...) This is because there is a certain rate at which water is being supplied to form drops, and a certain size of drop which can be suspended by the adhesion and cohesion of the water before it drips. The period is determined by the drop size divided by the flow rate. This is a linear relationship. It gets a little tricky because the drop size does interact with the flow rate a little, ( R. F. Cahalan, H. Leidecker, and G. D. Cahalan, "Chaotic rhythyms of a dripping faucet," Comput. Phys. 4, 368-383 (1990)) but the important thing here is that the drip rate is constant at low flow rates. A time series of a constant drip rate might look like figure 1.
Figure 1 - Time series for constant period
The period is all the same,
so you get a straight line. When you turn the flow rate up a bit,
the picture gets a bit more complicated. Instead of a constant
period, you get two different periods. (It sounds like da..dup....da..dup....da..dup....da..dup....da..dup....da..dup)
This is called period doubling. It looks like
Figure 2 - Time series exhibiting period doubling
This is evidence of period doubling, one of the routes to chaos. The higher rates of flow you get four bands across the time series or "period four" and then eight, and sixteen with the doublings occurring at an increasing rate. This is because the drop that is dripping does not get out of the way of the next forming drop in time and they begin to interact. The interaction is at first linear and occurs when the dripping drops cause the forming drop to oscillate.(Anyone who has spent any time watching a Lava Lamp has seen this in slow motion!) If the drip rate is fast enough, you enter a chaotic regime in which the drops seem to fall at random intervals (da da..dupdup dadup da dup da duppdup di di dup) A time series graph of this might look like:
Figure 3 - Chaotic time series
(It doesn't. I created this data with a computer program.) But these are not really random, the time series just makes them look that way. If you plot them with the nth drop as the x axis, and the n+1th drop as the y axis, you ( R. Shaw, The Dripping Faucet as a Model Chaotic System (Aerial, Santa Cruz, CA, 1984)) get a pretty picture. Figure 4 has a graph of the data from figure 3 plotted this way
Figure 4 - A chaotic strange attractor.
This is a strange attractor, (This is not dripping faucet data - it is the attractor of Henon) and this type of graph is called a Phase space plot. The points from figure 3 fall unpredictably on the pattern shown in figure 4, drawing a picture that is infinitely complex ( If you zoom in on any one line, it is made up of perhaps two lines, three and then two, and each of those lines are made up of two lines, three lines and then two and so on to the limit of precision.) and clearly not random.
My research question was whether the bubbles leaving a nucleation site (When you leave a pan of water on the stove boiling at a low level, nucleation sites are those spots that have little streams of bubbles leaving them. You also see them sometimes on the side of a glass of soda pop.) in boiling water were chaotic in the same way that drops leaving a leaky faucet were. My holy grail was a strange attractor; I would know that the time series data for bubbles was chaotic if I got a strange attractor when plotted in phase space.
Method Table of Contents
I decided upon a "double boiler" kind of arrangement, with an outer bath heated by coils of nichrome wire, and a vibrationally isolated inner bath where the experiment would take place. Into this inner bath I would put various heated objects likely to have nucleation sites. I would shine a laser through the whole thing, and the rising bubbles would interrupt the beam, allowing me to time their departure from the nucleation site using Transpacific's Universal Laboratory Interface (ULI). Figure 5 shows a cross section of the apparatus taken in the plane perpendicular to the laser beam.
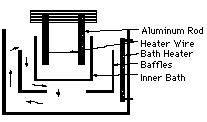
Figure 5 - Cross section of experimental setup. The arrows show the
direction of the circulating heated water.
The inner dimensions of the outer bath were 16" wide, 14" tall, and 6" deep, and the walls were of 1/2" polycarbonate plastic to withstand high temperatures. The outer bath was an ethylene glycol solution, and the inner bath was distilled water. The entire apparatus rested on a two-tiered isolation table of the poor man's type: a 1 1/2" x 24" x 32" slab of concrete on top of four wheelbarrow inner tubes on top of another slab of concrete on top of four more inner tubes. The vibrational isolation was important because chaotic systems are extremely sensitive.
Results and Discussion Table of Contents
Looking at the nucleation sites on a tightly stretched heater wire turned out to be a bust. The multiple sites on a wire would tend to communicate with each other and take turns nucleating. The rate of a particular site would oscillate up and down.
Figure 6 - Times series of a fluctuating nucleation site.
This is not what I wanted. I needed to look at one nucleation site operating independently to get the kind of attractor that the dripping faucet displayed. As I thought about this, I noticed a stainless steel screw that held the inner bath to its support nucleating with a constant period. It was a Phillips head screw with the head end in the inner bath, and the thread end immersed in the outer bath. I realized right away what was going on. The thread end was being heated, and as the heat conducted along the screw itself, in equilibrium, the deepest part of the cross-shaped indentation was the hottest. I quickly rigged up a heated screw to put in my apparatus where the laser could reach it. When I heated it up, nothing really happened with the screw, but one of the wires holding the screw began to nucleate like mad. In desperation I aimed the laser at this stream of bubbles and aligned the photo diode. It turned out to be the best data I would ever get. My time series data looked like:
Figure 7 - Potentially chaotic time series derived from a series of bubbles
leaving a holder wire on my setup.
This was sufficiently chaotic looking for me, so I plotted it as a phase graph and I got:
Figure 8 - Alleged strange attractor derived from the data in figure 7
Clearly, I was not seeing a random distribution of points. There were prominent areas of nothing as opposed to random distribution covering the plot frame more or less evenly. It also wasn't clearly a strange attractor, it might have been a blurred graph of periodic bubbling. Since multiple period dripping is a precursor to chaos, I was encouraged by these results. Already running late for the day, I shut down my experiment, and biked home, hoping to resume study of this nucleation site the next day.
The site never bubbled again for me. I tried a number of things after that, but never got a nucleation site as well behaved as my holder wire. With Summer 1997 drawing quickly to a close, I felt a bit desperate, so I tried blowing water vapor through a small hole in the end of a plastic tube. It wasn't a nucleation site, but it might show some signs of chaos, or pre-chaos. This would at least support the notion that a nucleation site would be chaotic, and it would give me a bit more to talk about in Tucson.
Although I never got a strange attractor, I did get some data that resembled period doubling behavior. One of the most promising time series looked like
Figure 9 - Time series from water vapor bubbles leaving a tube immersed in near-boiling water.
The four horizontal lines are evidence of period four behavior.
I intend to pursue possible chaos in streams of bubbles perhaps just using compressed air, and not nucleation. My apparatus for this experiment turned out to be just barely functional. In order to get the inner bath hot enough for boiling, the outer bath, even with its ethylene glycol, was always on the verge of boiling and would periodically bump, shaking the entire experiment. Using compressed air would eliminate this problem.
Acknowledgments Table of Contents
I would like to thank Jack Semura, Erik Bodegom, and Jean Murray of PSU for their technical help, Ed Saunders of TAP Plastic for making the apparatus itself, my wife Shannon for listening to me about bubbles, and my son Keenan for tolerating my absence. None of this would of course be possible without the generous funding from the Murdock Charitable Trust and the Research Corporation.
Links Table of Contents