Introduction:
The violin, along with many other musical instruments of its kind,
has been creating music for listeners of all kinds for centuries. The "classic
violin repertoire," as described by Alfred Doerffel, has been building
for years, all based on simple sounds produced by strings (Doerffel 160).
Besides the tones emitted by the strings, there is a multitude of other
facets to this complex instrument. A study of the violin, "an endlessly
fascinating instrument, both historically and artistically," is an insurmountable
task (Stowel 1). Therefore, we shall focus only on a single aspect of the
instrument. The different tones created by the strings are the direct result
of the frequency at which the string vibrates. With the help of an artificial
sound source, a function generator attached to a speaker, we will attempt
to predict modified pitches from a known open-string frequency.
A violin on its own is capable of creating what are known as sympathetic vibrations. A sympathetic vibration is created when a note matching that of an open string below is bowed. For example, if a D were to be played on the A string, the D string would vibrate sympathetically. Using this principle as a basis for research, we will attempt to create sympathetic vibrations for not only the open strings, but with fingers depressed using an alternate sound source. The source of artificially created sound waves will be such that it can be calibrated to emit a specific frequency. Verification that the string is sympathetically vibrating will be shown both by the vibration and the resultant echo in the instrument itself. In some cases, the string may not be visibly vibrating, in which case the vibration will have to be felt by a finger, lightly placed on the string. Incidentally, "trying to make music with an unamplified string," as stated by Carleen Hutchins in1962, "would be like trying to fan oneself with a toothpick" (Hutchins 81).
The tones for which we will attempt to find sympathetic vibrations will be a variety of "solid" tones. A solid tone is the creation of a new fundamental frequency by pressing a finger down on a string. This is different from a harmonic, which is created simply by lightly planting oneís finger at certain increments along the string. As defined by Microsoft Encarta 98 Encyclopedia, harmonics are a "series of subsidiary vibrations that accompany a primary wave motion." Beginning with the knowledge provided by Giancoliís Physics concerning fundamental wave frequencies of open strings (i.e. A 440Hz), we should be able to map out a wide range of note frequencies by calculation.
The Equation:
Before a test could begin, frequency predictions were first required.
An equation was needed that used only the little given information that
we had and produced a fairly accurate frequency. Therein lay the greatest
challenge of this project. The information that we began with was the frequencies
of the open G, D, A, and E strings (196 Hz, 294 Hz, 440 Hz, and 659 Hz,
respectively). The only other factor that we could measure accurately was
distance. The distance, in this case, was measured in centimeters from
the nut of the violin (the node of the open-string fundamental closest
to the scroll) to the finger that created the new note frequency.
Our first observation was that the pitch at the octave (twice the frequency of the open string) occurred at 16.4 cm. Thus, our first equation was set up using the frequency multiplied by an exponential of base two with a power of a measure length l divided by the octave. The equation for the A string, for example, was: f = 440 * 2^(l/.164). Though this did produce the doubling of the open-string frequency at the octave, this equation did not produce a doubled frequency at the next octave, half of the remaining distance (one fourth of the total length). We needed something more accurate.
Our next observation proved to break the equation barrier. It was not the length that was important, but the proportion. The frequency doubled at half of the total length and quadrupled at one fourth of the total length. This shows that the relationship between frequency and string length is an inverse proportion. Because any change would be inversely proportional as well, we were able to set up the following equality, where F, f, D, and d were, respectively, open-string frequency, resulting frequency, length of open string, and length of modified string: FD = fd. Solving for the sought after resulting frequency, we found that: f = (FD)/d. Though we did know the open string frequencies and the open-string length, the new distance was not that of the vibrating portion of the string. Therefore, we substituted (D-l) for d, producing the proportional equation: f = (FD)/(D-l). The dependent variable, f, could then be predicted with the substitution for l, the independent variable, while all other factors are kept constant. These constants were to mainly include the finger creating the notes (for consistent length measurements) and the external environment (to help ensure the maintenance of intonation). We could now begin predicting frequencies.
Experimentation:
To predict the frequencies, we played a note on the violin and measured
the distance from the finger to the nut. Putting the length into the equation,
we found the new frequency. After going through this process once, we realized
that it would be much more efficient to write a calculator program for
each string. After accomplishing this, all that was left to do was plug
l
into the program, and the calculator would solve for f. We decided
that it would be best to find the frequencies of each note on a single-octave
chromatic scale for all four strings on the violin. A chromatic scale consists
of 12 half steps. For example: G, G#, A, Bb, B, C, C#, is a segment of
a chromatic scale. Conversely, a major scale is comprised of both half
and whole steps. Now, ready to start taking down our data, we first set
up a chart on Microsoft Excel, allowing us to quickly record and evaluate
data. After recording distances, l was used to find the frequency
of each successive note. Once the calculator program suggested a frequency,
the function generator was calibrated to match it. The resulting pitch
resonated from the speaker. By holding the violin up next to the speaker,
sympathetic vibrations could be detected by placing a finger on the string
in question. In most cases, our calculations were correct, resulting in
the vibration of the string. In some cases, however, our calculations did
not end up producing a sympathetic vibration. We hypothesized that the
lack of vibration was caused by human error. In measuring l, great
care had to be taken, for a small error of even a tenth of a centimeter
could mean a difference of nearly two hertz. Factors contributing to an
error in measurement were most greatly concerned with the intonation of
the violin and of the individual notes.
After noticing a continuing trend of discrepancies between the frequencies of same notes on different strings (for example, the C on the D string and the A string), we thought it might be helpful to once again measure the distances on the strings. If we could take more accurate measurements, our answers would also be more accurate. To insure that the notes we were measuring were in tune, we added a further control group (one we should have noticed from the beginning); each note played was carefully checked against an electronic tuning device. This in itself was time consuming because a difference of 5 Hz could be produced just by slightly shifting the weight of the finger in one way or the other. We also took greater care in the measuring itself, because the first set of measurements seemed to indicate the necessity of greater precision. In taking the new measurements, we made them as accurate as possible by lining up the measuring tape nearest the point on the finger that was exerting the most pressure.
With the new and more accurate measurements, we then proceeded to recalculate the new frequencies. Not surprisingly, the new calculations coincided with each other much more consistently, and notes of the same frequency, but on different strings, only disagreed by no more than 4 Hz. With the notes now in agreement, our last step was to check them against the function generator. For greater accuracy, each generated note was checked with the electronic tuner instead of sympathetic vibrations, which require less accuracy of frequency in order to vibrate. Our results were very encouraging, for none of the calculations were higher or lower by more than 2 Hz (a total error of only 4 Hz).
Evaluation:
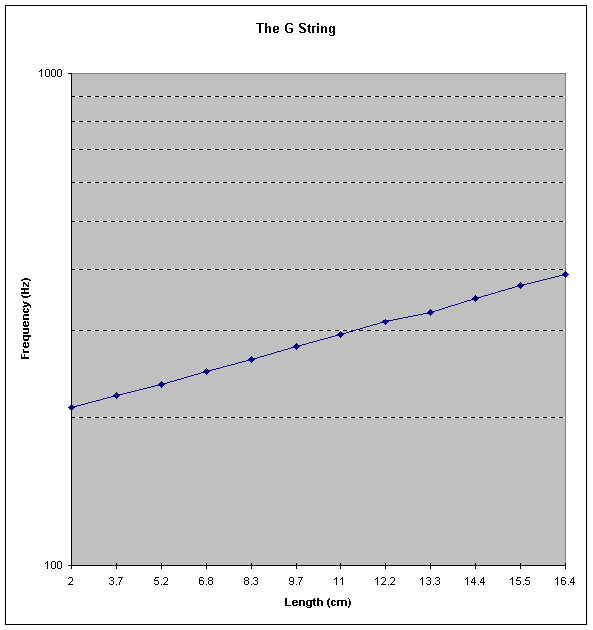
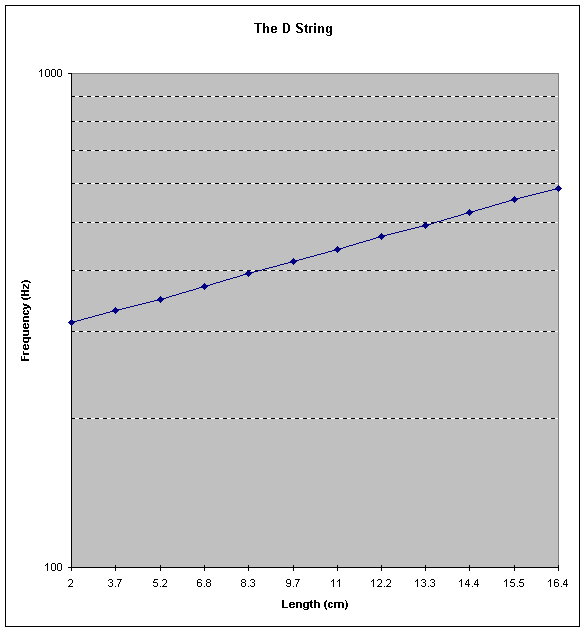
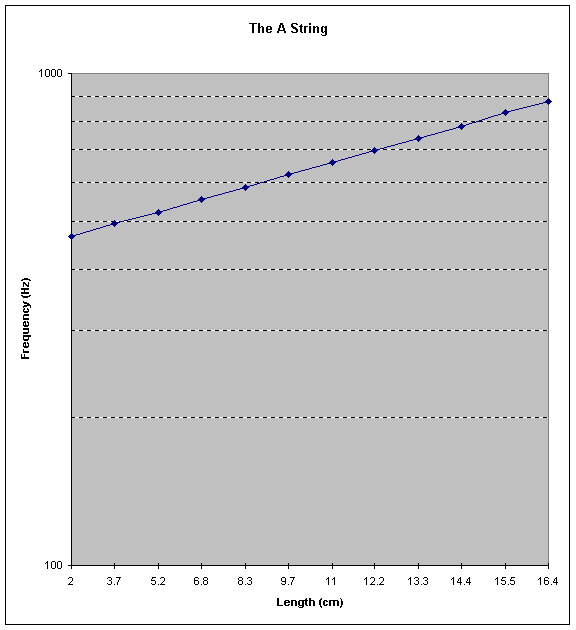
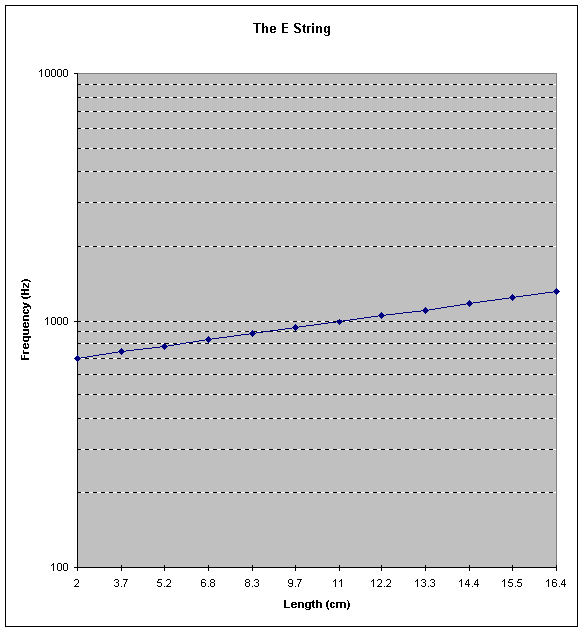
The final step was to interpret our data in such a way for it to have
special meaning. With the success of the frequency-generating equation,
we have successfully shown that the individual notes can be predicted,
but it was to the greater knowledge of the physics of the violin that we
sought to contribute some insightful information. In deriving our equation,
it was noted that as a violin string was ascended, shorter distances were
required to generate increasingly higher frequencies. This, it was reasoned,
must take the form of a logarithmic graph. If this proved to be true, the
data, when graphed on logarithmically scaled paper, should produce a straight,
upward slanting line. This is where Microsoft Excel came in especially
handy. Using this software, we were able to generate a graph for each string
using the compiled data. Aside from only a slight variation by one or two
points of the twelve, what the software showed were straight lines.
Mapping out frequencies for the violin (or any string instrument, for that matter) is, indeed, possible, as our successfully tested predictions have shown. Fundamental in reaching this auspicious conclusion were the derivation of a proportionality equation and the program that expediently calculated the new frequency. Not only was our attempt at mapping out a variety of frequencies successful, but we were also triumphant in using the information in such a way to support an earlier hypothesis.
We have also opened the door, at least to ourselves, for further research in this area. First, there is the possibility of the elimination of error. Though we were able to predict frequencies within two hertz of the actual note, an amazingly small amount of error, further steps could be taken to minimize this bound. The greatest point of discrepancy lay at the point of measurement, the finger. It was difficult to perceive exactly what part of the finger was responsible for the correct note frequency. Though the middle of the finger was appropriate for a fairly accurate guess, using a tool of greater precision to hold down the string would have allowed for more accurate readings. In addition, a function generator of more specific and accurate tuning mechanisms would have allowed for a more dependable frequency output.
Other possible areas of research include a simple expansion of our experiment.
This would entail a possible mapping of every note along the string, up
to the end of the fingerboard. However, as our data shows, the increments
between notes would become exceedingly small. This would make accurate
measurements require more precise instruments, as entailed by the suggestions
for decreasing the error. Nevertheless, the results from this particular
experiment were astounding, especially considering the small margin of
error. And though our success may go unnoticed, the violin is sure to continue
to make beautiful music for centuries to come.
Raw Data: text file containing data
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| Length cm | Frequency Hz |
|
2
|
209
|
|
3.7
|
221
|
|
5.2
|
233
|
|
6.8
|
247
|
|
8.3
|
262
|
|
9.7
|
278
|
|
11
|
294
|
|
12.2
|
312
|
|
13.3
|
328
|
|
14.4
|
349
|
|
15.5
|
371
|
|
16.4
|
391
|

| Length cm | Frequency Hz |
|
2
|
313
|
|
3.7
|
331
|
|
5.2
|
349
|
|
6.8
|
370
|
|
8.3
|
393
|
|
9.7
|
416
|
|
11
|
441
|
|
12.2
|
467
|
|
13.3
|
493
|
|
14.4
|
522
|
|
15.5
|
555
|
|
16.4
|
586
|
| Length cm | Frequency Hz |
|
2
|
468
|
|
3.7
|
496
|
|
5.2
|
523
|
|
6.8
|
555
|
|
8.3
|
588
|
|
9.7
|
624
|
|
11
|
661
|
|
12.2
|
699
|
|
13.3
|
739
|
|
14.4
|
782
|
|
15.5
|
832
|
|
16.4
|
878
|
| Length cm | Frequency Hz |
|
2
|
702
|
|
3.7
|
743
|
|
5.2
|
783
|
|
6.8
|
831
|
|
8.3
|
882
|
|
9.7
|
935
|
|
11
|
990
|
|
12.2
|
1048
|
|
13.3
|
1107
|
|
14.4
|
1172
|
|
15.5
|
1247
|
|
16.4
|
1315
|
Giancoli, Douglas C. Physics: Principles with Applications. New
Jersey: Prentice Hall,
1991. 3rd ed: 316.
Hutchins, Carleen M. "The Physics of Violins." Scientific American
November 1962:
77-89.
Johann Sebastian Bach: Works for Violin. Toronto: General Publishing
Company, Ltd.,
Bach-Gesellschaft edition.
Rosenblum, Myron. "Harmonics." Microsoft Encarta 1998 Encyclopedia.
1998 ed.
Stowel, Robin. The Cambridge Companion to the
Violin. Cambridge University Press,
1992.
Links:
The physics of
sound
Violin
Harmonics
The physics
of Music
Sympathetic
vibratory physics
Superstrings
Violin acoustics