How the Length of a String Affects the Period
and Gravitational Acceleration of a Pendulum: Background | Materials | Procedure
| Data | Graphs | Conclusion
| Bibliography | Return to Research
Marissa Martin
From, keeping time, to
religious practice and recreation, the pendulum has been being used for
decades; however, many people are unaware of the complexities that come with
the pendulum as well as the physics behind it. For example, when one sees a
grandfather clock, they rarely focus on the pendulum inside and how it’s able
to swing from side to side repeatedly in exactly one second. When examined, it
becomes clear that this process is quite complex, as well as the pendulum
itself. To create a pendulum, there is a string or a massless rod that hangs
down vertically from an object/surface, or the “point of suspension,” and on
the bottom of the string is a bob or a weight that acts as the main mass of a
pendulum. Once put together, the pendulum is created and looks similar to Figure
A.
Figure
A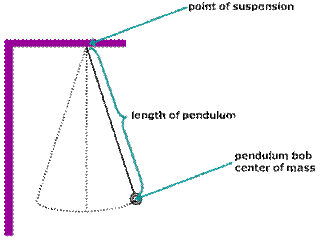
Though
it is simple in construction, the pendulum has many variables that can be altered
in order to receive different results, such as the length of the pendulum
string and the angle it is released in order to have it tick every second
exactly. With this concept in mind, I came up with a research question
involving pendulums; how does the length of the string affect the period and
gravitational acceleration of a pendulum? To test this, independent,
dependent, and controls will all be used. As explained about, the length of the
string will be the independent of the experiment, and the period and
gravitational acceleration of the pendulum will be the dependent variables. For
the controls of the experiment, the mass of the bob will stay at 1 KG, and the
pendulum will always be dropped at a 70 degree angle.
In
order to investigate how the length of a pendulum affects the period and
gravitational acceleration of a pendulum, one will need the materials listed
below:
- Paper
- Calculator
- A timer
- A pencil
- A computer with internet access
- An online pendulum simulation (the simulation must have
a way to alter the length of the string as well as chose the angle at
which the pendulum falls)
![]()
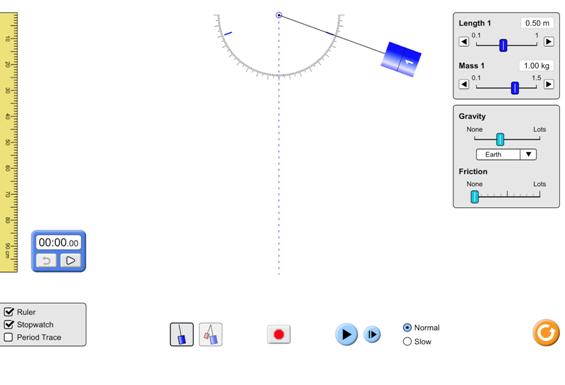


Simulation
Procedure Top
Before
you start, make sure you have a computer, a pencil, paper, and a timer at hand.
The first step to the experiment is logging on to the computer at hand, going
on any search engine, and looking up “pendulum simulation.” Browse through
various simulations until you find one that allows you to change the length of
the string and see the angle at which you place your pendulum. Once this
is done, take a piece of paper and make a data table with your pencil, with two
columns (label one length in meters and the other time in seconds), and 10 rows
(start at trial 1, and count up to trial 10). Once the data table is made, use
the simulation to make your string length 0.10 m, write the length in your data
table, make sure the mass is 1.00 kg, and place the pendulum at a 70 degree
angle. When you release the pendulum, press start on your timer. Keep the timer
as you watch the pendulum sway back and forth 12 times (starting at left, to
right, and back to left is one (one oscillation)). Once you reach 12, stop the timer,
and write the seconds in the time column for trial 1. For trials 2-10, repeat
the same process as trial one, but increase the string length by 0.10 m each
trial. Continue to place the pendulum at 70 degrees, counting 12 oscillations,
timing how long it takes, and recording the data in the corresponding spots.
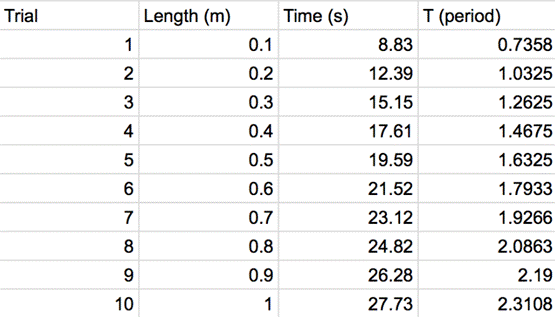
After using the online pendulum simulation,
here is the raw data I collected for how the time of the pendulum through 12
oscillations is affected by the length of string.
T=t/12
is then used to calculate the amount of time it took for the pendulum to
complete one full oscillation, or the period
Next, g=4pi^2L/T^2 is utilized to
calculate the gravitational acceleration for each trial, where L is length and
T is period based on the trial
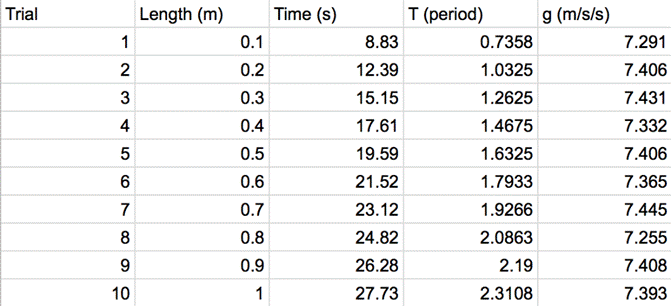
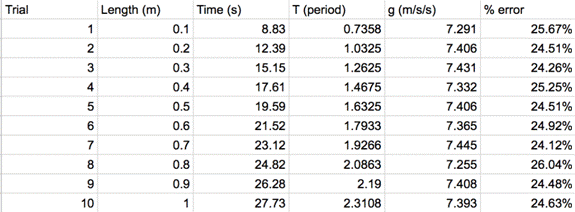
Once each gravitational acceleration has been
calculated, find the % error by using ( |9.81-g|/9.81)*100 for each g
value (9.81 m/s/s is used as the accepted value for gravity).
Graphs Top
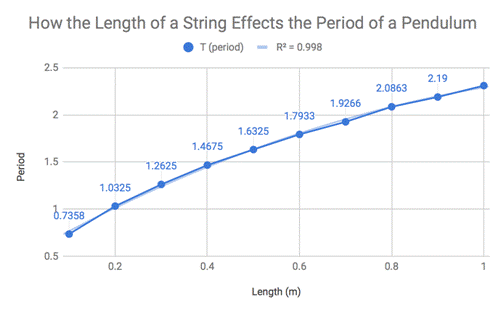
Conclusion Top
For
this research assessment, I decided to investigate the question of how
the length of a string affects the period and gravitational acceleration of a
pendulum. Once doing my experiment, copying the data, and calculating the
various, I have come to a conclusion. When you increase the length of the
string on the pendulum, the period also increases; however, the gravitational
acceleration isn’t affected by the length of the string, but is more so stays
fairly constant the whole time. As shown in the data tables and also in the
first graph above, the period of the pendulum increases steadily as the length
is also being increased. Since the data was gathered from an online simulation,
it seems reliable as there are minimal ways one can accidentally alter the data
in a negative way. However, the small increase of the string length (being from
0.10 m to 1.00 m) may have limited the data as it could begin to change later.
Additionally, the timing of how long 12 oscillations took may have been
slightly off which would weaken the data and alter it
overall.
As
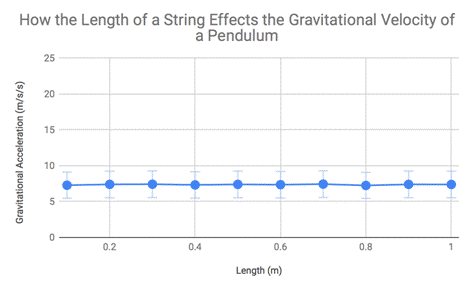
for the gravitational acceleration, it appears to remain somewhat constant the
entire time, meaning that the gravity on the pendulum has little to no change
when the string length is increased and/or decreased. But, with the knowledge
that accepted gravity is 9.81 m/s/s, and all of these gravitational
accelerations are within 7.2 m/s/s and 7.4 m/s/s, the question of errors in the
experiment rise. If the timing of the oscillations were originally off, then
the data for the gravitational acceleration will also be somewhat incorrect.
Additionally, there could have been miscalculations when using the equations to
determine the acceleration.
Overall,
throughout this investigation, I had to work through various problems and learn
how to do a thorough investigation/lab by myself, ultimately resulting in
interesting data. When you increase the length of the string on a pendulum, the
gravitational acceleration stays almost the exact same, while the period
steadily increases as it has farther to travel with the same starting angle.
Furthermore, if your grandfather clock was counting seconds faster than it
should be, you can increase the string length in order to increase the time it
takes to complete a period.
PhysicsLAB: Ripple Tank Sample Solutions,
dev.physicslab.org/Document.aspx?doctype=2&filename=OscillatoryMotion_ClassPendulums.xml.
This is a webpage that
explains the motion of the pendulum as well as offers an online simulation
OpenStaxCollege. Introduction to Sociology – 1st Canadian Edition, BCcampus, 23 Jan. 2012,
opentextbc.ca/physicstestbook2/chapter/the-simple-pendulum/.
This link discusses
the angular acceleration of a pendulum in regards to gravity
“Pendulum Motion.” The Physics Classroom,
https://www.physicsclassroom.com/class/waves/Lesson-0/Pendulum-Motion
This link is very helpful for understanding a pendulum,
it’s motion, and the factors that effect it.
“Pendulum Motion.” The Physics Classroom,
https://www.scientificamerican.com/article/bring-science-home-swinging-pendulum/
The awesome,
interesting science behind a pendulum
“Pendulum Lab.” PhET,
https://phet.colorado.edu/en/simulation/pendulum-lab
A
pendulum lab simulation