The Affect of Sugar Concentration on the Index of Refraction .:. Go Up

Alexander Dyer

 

Introduction   Hypothesis   Scientific Reasoning   Independent Variables   Dependent Variables   Controlled Variables   Equipment   Diagram of Setup   Procedure   Method of Analysis   Analysis   Calculations 1   Angle of Refraction   Calculations 2 (Electric Boogaloo)   Index of Refraction   Calculations 3 (Ron Moholt)   Conclusion   Limitations   Links   Citations   

 

 

Introduction: Go Up

            The goal of this investigation is to determine the relationship between the density of a liquid and the index of refraction. Refraction occurs when light goes through two transparent mediums of different index of refraction values. When light enters the new medium at any angle, different than perpendicular with the medium, the light will change its direction, or bend, also known as refraction. The reason this scientific change in direction of light is interesting to me is because of the optical illusion side of refraction. I find it incredibly interesting that an object can appear bigger, or even bent within water, so I needed to find out why that happened. I would eventually discover that the reason this optical illusion existed was due to refraction. The reason that these objects would appear to be bent or bigger was the result of two different index of refraction values of the two different mediums. Since air and water have two different index of refraction values, which describes how fast light travels through the medium, the objects would appear bigger or bent. Knowing how this illusion works, I furthered my curiosity by wondering how adding sugar to water would affect the index of refraction for the water. For this investigation, I decided to determine how sugar concentration in water would affect both the angle of refraction and index of refraction for water.

 

Hypothesis: Go Up

If the sugar concentration within a sample of water is increased, then the angle of refraction  decreases and the index of refraction increases, because the density shall be increasing do to the sugar concentration.

 

Scientific Reasoning: Go Up

 As light passes through different mediums of different densities, then the angle at which the light is moving shall change, this is called refraction. This is due to a change in the index of refraction, so by changing the density of the liquid I am shining a light into, by adding sugar, then the refractive index should change, which will in turn make the angle of refraction change with it. Based on Snell’s law, it’s  clear that if index of refraction increases, then the angle of refraction must decrease, and vice versa. This is clear since the equation must balance out on both sides, so if one variable increases on one side, then the other variable on that same side must decrease, in order to balance the equation.

 

Independent Variable: Go Up

 The density of the water solution.

 

Dependent Variables: The angle of refraction, and index of refraction.

●        Index of refraction shall be discover through Snell's Law:

●        Angle of refraction will be evaluated through the formula

 

Controlled Variables: Go Up

1.      Temperature of the medium

a.    Reason for control: The temperature of a liquid is a determinant of its density. If the temperature of the medium increases or decreases, then the density will change. This would lead to a change in the index of refraction which would change the the amount that the light bends in the new medium.

b.    How to control variable: In order to ensure that the liquid stays at room temperature (20 ± 1 celcius), a thermometer will be used with each new solution of the medium.

 

2.      Angle of Incidence

a.    Reason for control: The angle at which the light enter hits the medium will then affect the angle at which the light bends within the new medium, as can be observed through the formula. Since a different angle going into the medium will affect the angle at which it will bend in the medium, a controlled angle will be needed to get the most accurate results.

b.    How to control variable: This will be accomplished by using a pole and clip to hold a laser pointer at a consistent angle so that the angle will not be subject to change.

 

Equipment: Go Up

 

●        Laser pointer

●        1 pole for laser pointer stand

●        Clip to hold laser pointer

●        Meter stick

●        Triple Beam balance

 

●        Container that will hold the liquid

●        Wax paper

●        Sharpie

●        Sugar

●        Measuring cup

 

 

Diagram of setup: Go Up

 

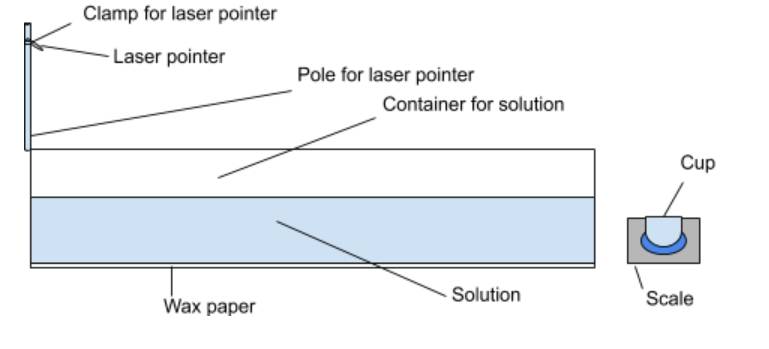
Procedure: Go Up

            The first step in this investigation was to gather all the necessary equipment and set it up as dictated in the above diagram. After making sure the equipment was set up correctly, I would then measure the cup, then add sugar and write down the values I got from the measurements. I would then subtract the cup mass from the mass of the sugar and cup, so that I could find out how much sugar I added. After doing this I would ensure that the temperature was still at room temperature. I would then make sure all the sugar had dissolved within the water before I would shine the laser pointer from the pole. Once dissolved, I would turn on the laser pointer and mark where it hit the bottom of the wax paper with a sharpie. I would repeat this process for 10 data points, to ensure the best data possible. After making all the data points in the water, I removed the wax paper from the bottom of the container and measured the distances with a meter stick, and noted the measurements for each point on piece of paper.

 

How Refraction was analyzed: Go Up

 

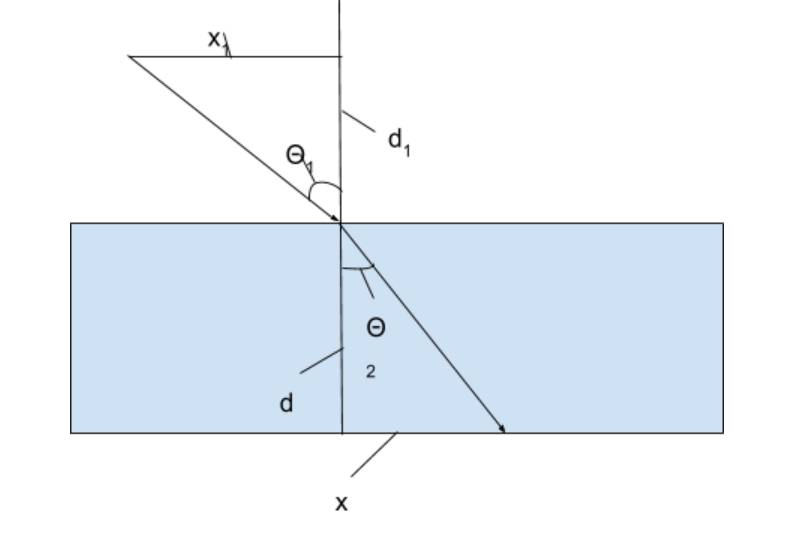
            Refraction patterns were analyzed by measuring the distance the light traveled across the water, and down. By using these measurements, the angle of refraction could be discovered and in turn, the index of refraction. There was a sharpie mark where the light entered the water, and where it hit the bottom of the container. This was used to find how far the light traveled in the water from the entrance point. The height of the water in the container was also measured so that the angle could be found. The angle of incidence was measured through similar means of measuring the height and distance the laser pointer was from the point it hit the water.The index of refraction was then measured by using Snell’s law and using the angles of refraction and incidence that was observed.

 

 

Analysis: Go Up

 

Density of the Solutions

            At the start of each new trial, the mass and volume of the solution would be noted as to find the density through the density formula. Density is ρ, volume is v, and mass is m. By doing this I was then able to find the uncertainty of the solution’s density.

 

Amount of Sugar in the solution         (.05 g)

Mass of the Solution including Cup

(.05 g) m1

Mass of Solution

(.05 g)

m

Volume of the Solution

(10 mL)

v

Density

(g/mL)

Percent Uncertainty

Density % uncertainty

0

1025.4

952.6

952.6

1.000

.005774

.006

224.4

1249.8

1177

952.6

1.23557

.00701

.007

471

1496.4

1423.6

952.6

1.49444

.008369

.008

749.6

1775

1702.2

952.6

1.7869

.009904

.01

939.8

1965.2

1892.4

952.6

1.98656

.010952

.011

1137

2162.4

2089.6

952.6

2.19358

.012039

.012

1352.1

2377.5

2304.7

952.6

2.41938

.013224

.013

1538.8

2564.2

2491.4

952.6

2.61537

.014252

.014

1878.7

2904.1

2831.1

952.6

2.97197

.016124

.016

2274

3299.4

3226.6

952.6

3.38715

.018303

.018

 

Calculations: Go Up

            The first step was to determine the mass of the solution, this was accomplished by subtracting the measuring cup’s mass by the mass of the cup and mass of the sugar together. By measuring the cup, I determined the mass of the cup was 72.8 .05 g.

 

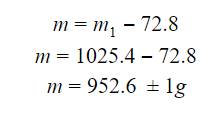
            Once the mass of the liquid was determined, the next calculation was to calculate the density. To do this I The density of the liquid was determined using the formula: 

 

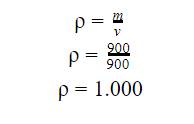
From the volume and the mass, the total percentage of uncertainty would be evaluated for the density.

 

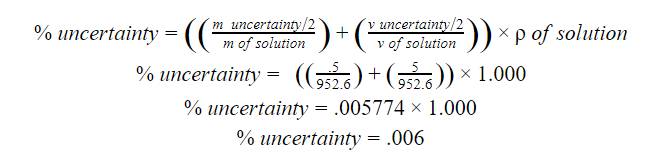
Note: These calculations were repeated for each amount of sugar added to the overall solution

 

 

DATA: Excel and Text

 

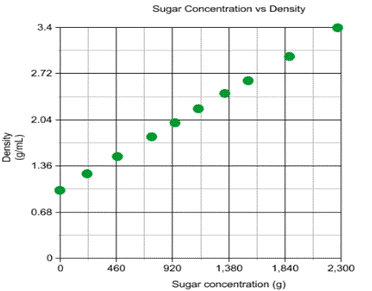
The graph depicts the relationship between the amount of sugar in the solution, and the density of the solution. Unsurprisingly, as the amount of sugar increased, the density of the solution also increased. This increase in density is due to the increase of mass within the same volume, which can be understood through the formula .

 

 

 

Angle of Refraction Go Up

            The next step after calculating the density, was to determine the angle of refraction and the angle of incidence. These were the next calculations to be made in order to set up for the calculation of the index of refraction.

 

Distance down in air    (.05 cm)

Distance across in air  (.05 cm)

Angle of Incidence

(1°)

Distance down in solution

 (.05 cm)

Distance across in solution

 (.05 cm)

Angle of refraction

(1° )

20

32

57.99

8.9

8.4

43.34

20

32

57.99

8.9

8.1

42.31

20

32

57.99

8.9

8

41.95

20

32

57.99

8.9

7.5

40.12

20

32

57.99

8.9

7.4

39.74

20

32

57.99

8.9

7.3

39.36

20

32

57.99

8.9

7.1

38.58

20

32

57.99

8.9

6.8

37.38

20

32

57.99

8.9

6.5

36.14

20

32

57.99

8.9

6.1

34.43

 

 

Calculations: Go Up

 

            Before I calculated the angle of refraction, I chose to calculate the angle of incidence, which was the angle at which it is coming in at the solution. This calculation was done by using the formula .

 

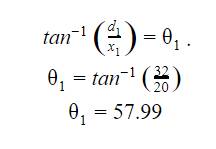
After calculating the angle of incidence, the next calculation was the angle of refraction, this was accomplished by using a similar formula that was used for the angle of incidence, except with using measurements from within the solution.

 

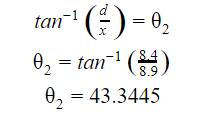
Note: Calculations were repeated for every new measured distance.

 

 

DATA: Excel and Text

 

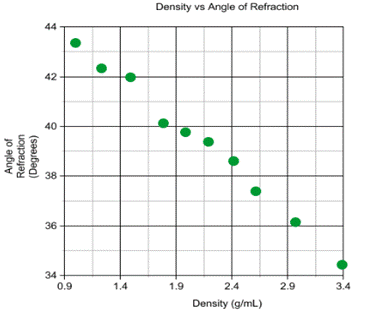
This graph depicts the relationship between the density of the solution and the angle of refraction. The graph shows that as the density increased, the angle of refraction would decrease.

 

 

 

Index of Refraction Go Up

The final calculations for this investigation was the index of refraction. By calculating this last value, I would then be able to complete prove or disprove my proposed hypothesis.

 

Index of Refraction for air

Angle of Incidence

(1°)

Angle of Refraction

(1° )

 

Index of refraction for solution

Index of Refraction for solution % uncertainty

1.00029

57.99

43.34

1.33838

.02798

1.00029

57.99

42.31

1.37124

.02803

1.00029

57.99

41.95

1.38282

.02841

1.00029

57.99

40.12

1.44592

.03049

1.00029

57.99

39.74

1.45969

.03085

1.00029

57.99

39.36

1.47389

.03143

1.00029

57.99

38.58

1.50362

.03245

1.00029

57.99

37.38

1.55188

.03414

1.00029

57.99

36.14

1.6051

.03605

1.00029

57.99

34.43

1.68508

.039

 

Calculations: Go Up

            Finally to the calculation that was the purpose of this investigation, I calculated the index of refraction for the solution. In order to calculate the index of refraction in the solution, I used snell’s law: .

 

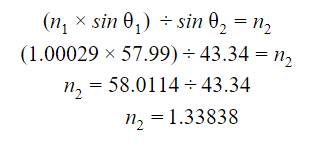
            The final calculation for this investigation was the percent uncertainty in my calculated index of refraction values. Calculating the % uncertainty in the Index of Refraction value would use the same uncertainty formula as used for density, but in terms of the index of refraction.

 

 

 

DATA: Excel and Text

 

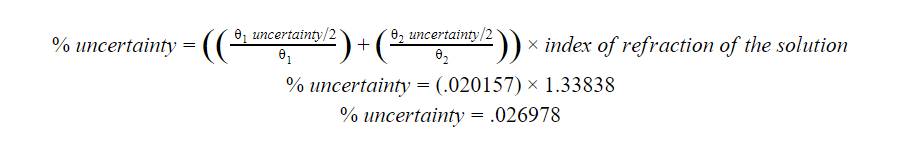
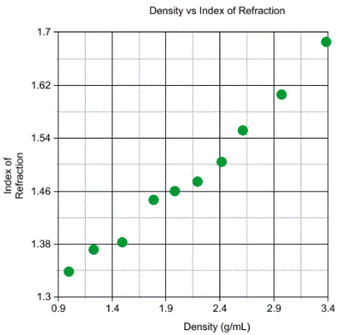
This graph depicts the correlation between the  index of refraction and the densities that is received. This relationship shows that as the density increases, then the angle of refraction increases as well.

 

Conclusion Go Up

 

            Based on the data and calculations I made throughout the investigation, it is evident that my hypothesis was correct. This investigation was able to prove that if a substance, such as sugar, is added to water, then the density will increase, which will also increase the index of refraction value for the water, and also decrease the angle of refraction. Index of refraction is directly connected to the density, since as density increases, as does the index of refraction. Based on this relationship, it can be determined how the index of refraction could be affected in other substances based on their densities. The denser the medium, the higher index of refraction value that medium will have. This relationship also tells a lot about the relationship between density and the angle of refraction. Since the index of refraction increases with the density, that makes the angle of refraction decrease with the density. This investigation ultimately concluded that as density increases index of refraction will increase, and the angle of refraction will decrease.

 

Limitations Go Up

            One limitation from this investigation was the thermometer; this could have been a limitation in the investigation because the thermometer could have been reading an incorrect temperature. Even though this is an unlikely error that could have occured in the process of this investigation, it is possible that it happened. If the thermometer was indeed misread or off, then it would change the calculations that I got for each variable. Temperature affects the density of a liquid, with colder temperatures increasing the density and heat increasing the density. If the temperature was not being told correctly by the thermometer, then it is possible that the data could have been skewed by the mistold temperature of the solution. A solution to this possible error in the investigation is the use of an electronic thermometer, or the use of multiple thermometer to get multiple reads on the temperature. By using these methods, this error could reduced in the investigation.

            Another error that could have occured during the investigation was residue being added to the water solution that was not desired, from the wax paper and sharpie. The wax paper was used so that I could record how far the light travelled horizontally in the water, as was the sharpie used to notate where light hit the wax paper from the set entrance point. It's possible that the wax paper would start to leave traces of other materials in the water. This was a possibility as well when the sharpie was put in the water to mark where the light was shining. Ink would go into the water each time it entered. Both of these errors would lead to an increase in density, which as addressed earlier, would lead to increase in index of refraction and decrease in angle of refraction. This possible increase in densities would lead to another possible skew in the data. A possible way to fix this is to use materials that do not leave residue in the water, or by making the markings on the outside of the container, so that the water itself is not contaminated.

            Another error that could have occured during the process of this investigation is if the clip that is holding the laser pointer changed slightly. If the the clip changed even a little bit, then the entire data set would have to be to be restarted so that the same angle of incidence was used for the entire data set. This could be changed by using a clip that is hard to move, but even with this solution, moving is still a problem. The best way to deal with this problem, would to measure the distances that the laser is from the water each time before taking the water measurements. By doing this, it would ensure that the same angle of incidence s used the entire time, and it would come to the investigator’s attention when the angle of incidence changes. With this it would allow the investigator to know when the data would be no longer valid.

            A final error that could have occured during this investigation was the assumption that the water being tested was pure water with no other chemicals with in the water. Granted that the density calculation showed that it was the density of the water, that does not mean that there were chemicals in the water that would be added from the air as time passed on, overall increasing the density. This would also change the results that would be given through the investigation, making the results less accurate.A possible way to make the results more accurate and to eliminate this error, a vacuum chamber would be optimal. This would ensure that no other micro-objects enter the solution, leading to a more accurate result.

 

Links Go Up

 

This is a viedoe that helps with understanding refraction and how to apply Snell’s Law: https://www.khanacademy.org/science/physics/geometric-optics/reflection-refraction/v/refraction-and-snell-s-law

 

This is a large index of refraction that helped ensure that my results made some logical sense: http://hyperphysics.phy-astr.gsu.edu/hbase/Tables/indrf.html

 

Provided a small index of refraction to check against other sources and provides other interesting facts about refraction: https://en.wikipedia.org/wiki/Refractive_index

 

Another informative site about refraction, but also has a simulator for refraction, where you control the index of refraction and the angles: http://hyperphysics.phy-astr.gsu.edu/hbase/geoopt/refr.html

 

Provided basic knowledge and understanding of refraction: https://en.wikipedia.org/wiki/Refraction

 

 

Citations Go Up

“Refraction.” Physics: Principles with Applications, by Douglas C. Giancoli, Pearson Education, 2005, ……..pp. 312–644.

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

Go Up

 

Congratulations, you found the Ron Moholt Easter egg

 

I love you Ron Moholt, you are the best of us and bring light the darkness of the Tualatin Band program. You always help us achieve our very best, and for that we love you Ron. Thank you for all the work you do Ron, you will live forever in our hearts.