IA: Projectile Mass vs. Initial
Velocity
Contents:
The
trebuchet is a mechanical siege weapon, similar to the catapult that has seen
predominant use in middle-aged battle, primarily during the Dark Age.
Trebuchets are powerful slingers that use the mass of a counterweight to use
gravitational energy to swing its arm, employing the projectile. Some uses were
for wall penetration in castles, and the hurling of heavy objects. Sometimes,
trebuchets would be loaded with area attack projectiles for purposes other than
direct destruction, some examples being bodies of the deceased, particularly by
the black plague. Of course, weaponry has since evolved from its current state,
and thus the only practical uses for trebuchets are through science
experimentation and recreation for historical purposes.
The
trebuchet was first invented in China around 300 B.C but didn’t see large use
in comparison to its already popular counterpart: the catapult. The French were
the first to utilize trebuchets in large quantities 800 years later. These
machines lobbed projectiles with masses of 110-220 lbs. and could be launched
as far as 1000 feet. The Large recorded arm length for a trebuchet was 60 feet
in length. Trebuchets were mobilized through deconstruction and reconstruction
of the machine in order to create mobility.
As
for the use of a trebuchet in this experiment, it can be assumed that certain
factors of use may increase and or decrease the success of the launch. In
practical use, having optimal velocity and distance would be useful to armies,
as making the best use of their machinery would be necessary. A factor that is
especially important is finding the right mass for your projectile. In the same
way, different bowling ball masses work with different effectiveness,
projectile mass could have an impact on the effectiveness of the trebuchet. In
order to measure this accurately, I will keep the counterweight on the trebuchet
constant.
Construction of the Trebuchet: Top
Due to
limitations in time and purchasing power, it is necessary that the trebuchet is
easily constructive and practical at the same time. I began by looking for
pre-made designs online and then rendering an Autodesk Inventor image of what I
imagined such would look like. The construction was composed of MDF (Medium
Density Fiberboard), which is a bit softer and easier to cut using a band saw,
and sections of flat board pine. MDF is also good against cracking under
pressure, which is important when drilling.
A circular
bearing is used to hold the fulcrum. These bearing are normally used for smaller
wheels, but their mobility while allowing for a proper swing of the trebuchet.
The pocket where the projectile is held is constructed of a fabric pouch and is
held onto the arm beam via. Eye Hooks. The entire cutting was done at the
workshop at TTOA,
with the use of drills, and a band saw. All construction was completed safely
and under proper supervision.
Cad Image Predesign of Trebuchet:
Diagram I

Changes made to the original design
of the trebuchet: Top
A trebuchet normally has a design where the projectile is
held in a pocket towards the end of the swinging arm. Due to limitations in my
design, and the rather small mass of my projectiles, I found that the pocket
simply would not launch the projectile in the linear fashion, and, instead the
projectile would fall backward. This made it difficult to collect the data I
had needed, and thus, I instead removed the ordinary pocket and used instead of
a plastic spoon at the end of the arm. This was stapled to the end using a
staple gun. The trebuchet worked effectively from then on, although its
original construction was makeshift. The spoon, however, made for good
placement as it fit my play dough projectiles with ease.
To find what effect projectile mass has on initial velocity
and horizontal displacement.
I anticipate that the greatest range
of the trebuchet will be achieved when there is:
A larger sized projectile. I believe
that my results will form a parabola with the maximum being on the higher end
of the spectrum. I believe this because higher masses are less likely to be
affected by air pressure, although very high masses would not be supported by
the counterweight.
Equations used for my experiment: Top
1. Linear Kinematics
In my experiment, we are attempting to find the velocity on
release by the trebuchet. Because the projectile is fired at an upwards angle,
both horizontal and vertical velocity are at play. Since this is the case, it
can be treated as 2 different equations.
Of our SUVAT equations, we will be using s = ut + (˝)at^2. This will get us our displacement.
We can
also make the assumption that when uniform, the angle of release by the
trebuchet will be 45 degrees, which is assuming its uniform every time.
2. Horizontal Factors
If we only
account for horizontal velocity, then we can pretend that the vertical part
doesn’t exist, but we would still account for gravity pulling the projectile
down. Using this method, we can find time of projectile flight, another
necessary component of the suvat equation.
3. Accounting for PE and KE
We know that energy can not be created or destroyed, as this
is the first law of thermodynamics. Because this is the case, we know that our
counterweight has certain amounts of potential energy when held back before
launch. Since we make the assumption that the is no potential energy before
launch prep, we can assume the equation is
As the
counterweight falls, that potential energy becomes kinetic. Now, we can make
the assumption that the projectile e fire has that same kinetic energy. If that
is the case, then our final equation is
Result Table: Projectile mass vs.
Initial Velocity & Displacement
|
Projectile Mass (Kg) |
Displacement (m) |
Initial Velocity (Calc) |
|
.01 |
8.4 |
6.5532 |
|
.02 |
6.7 |
4.4605 |
|
.03 |
4.4 |
3.5616 |
|
.04 |
4.2 |
3.0361 |
|
.05 |
3.6 |
2.6824 |
|
.06 |
3.3 |
2.4243 |
|
.07 |
2.6 |
2.2255 |
|
.08 |
2.5 |
2.0665 |
|
.09 |
2.5 |
1.9357 |
|
.1 |
2.1 |
1.8258 |
Velocity slows down very fast at first, especially when
weight of the projectile is 0.01 – 0.03kg; Beyond this, and throughout the
curve and likely beyond, the velocity does slow down, and this makes sense.
Counterweights must be proportional to their mass to get best intended effect
.We can assume that at some point, the pocket of the trebuchet would simply
flip, and we would left with an initial velocity of zero.
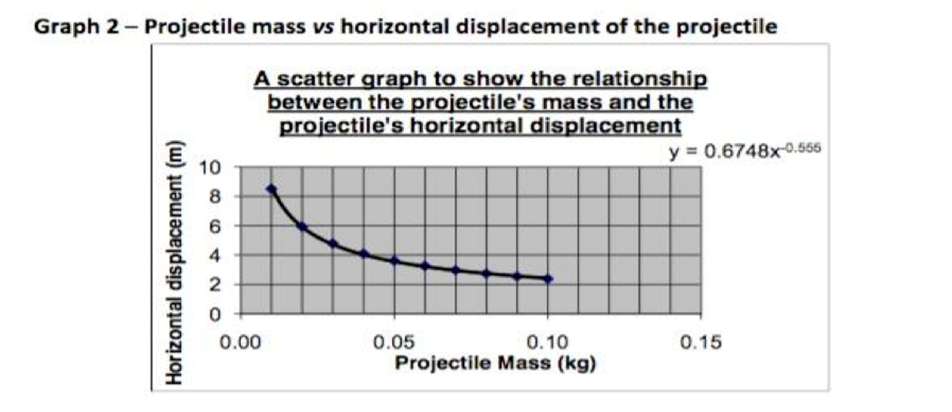
Graphs 1 and 2 clearly show that the initial velocity of the
projectile and because of so, the displacement horizontally, is proportional
The shape of the created graphs allows us to see something
that resembles a logarithmic curvature. This exponential decay could be
outfitted if need be. In the case of displacement, results were a little more
no uniform, which is to be expected, as the projectiles have to resist against
wind friction and displacement created against it.
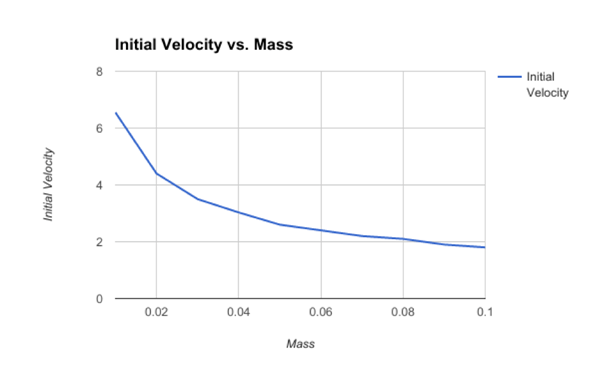
It can be concluded that smaller mass objects have
relatively higher initial velocities, and thus can be hurdled further
distances. This correlation does level off however, and the difference between
a larger mass object and a slightly heavier object may have little difference
when thrown.
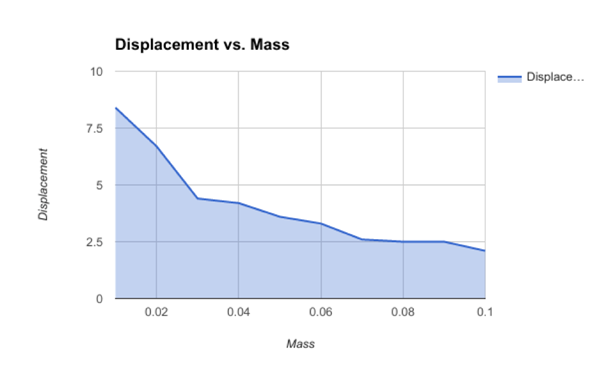
Due to the simplicity of the experiment, the only other
variable being measured was the masses being used as projectiles and
counterweights. Scales are by no means perfect, and we can make the direct
assumption we have uncertainty there, and after checking, the scale had an
uncertainty of .5*10^-4 Kg, which is small, but could still be a little
problem.
Unfortunately, not all of the masses were of the same size
and shape (Molded in play-dough by hand) so air friction couldn't really be analysed. This is another source of further potential
investigation if more time and researching power was available during this
experiment. The use of many different shaped projectiles all with the same
mass, such as something like rubber balls, would allow for a calculation as
such. This would also improve the accuracy of my results, as sticky play dough
may have stuck to the launcher.
If I had the opportunity to do the experiment again, an
alternative distance measuring method could involve the use of a video camera
along with physics software that can use reference for measurement. This would
allow for very accurate results that would be much more effortless. This could
also allow me to take other measurements, such as angle on release,
inconsistencies in the trebuchets design and more, things I could not account
for using the naked eye and an iPhone camera.
Generally, although my results are by no means 100%
accurate, looking at the graphs and the results obtained, I think it can be
said with certainty that as the projectile mass decreases, initial velocity and
distance increase.
Links: Top
http://www.lordsandladies.org/trebuchet.htm:
A website where you can learn more
about the use of trebuchets throughout history
http://www.physicsclassroom.com/class/1DKin/Lesson-1/Speed-and-Velocity
A great resource for getting a
better understanding of the math
A great khan academy video for
applying the knowledge of kinematics
https://www.scientificamerican.com/article/build-a-mini-trebuchet/
Build your own trebuchet and
experiment too!
https://www.autodesk.com/products/inventor/overview
Download inventor: a great tool for
bringing 3D design to life
"Trebuchet." Wikipedia. Wikimedia Foundation, 06 Apr.
2017. Web. 07 Feb. 2017.
"Trebuchets You Can Make."
How to Build a Trebuchet. N.p., n.d. Web. 07 Feb. 2017.