IB Physics Internal Assessment
May 2017
Kate Intile
The effect of inclination and pace on the force exerted by a distance runner’s foot:
Intro ∙ Newton’s Second Law ∙ Design ∙ Hypothesis ∙ Data ∙ Graphs ∙ Conclusion ∙ Bibliography ∙ Links ∙ Go up
Introduction Back to the top
I am a competitive distance runner, which means injuries are just inevitable. Last track season, unfortunately, I developed a stress fracture in my shin. Many trips to the doctor’s office concluded that the fracture was caused by impact. Whether my shoes were too old, or I was running on the wrong surfaces was completely unknown. As I battled through the fracture for the remainder of the season, it was a guessing game as to what kinds of terrain I could run on, and if I could run on it at all. Was I running too fast on it, or would running too slow cause larger impact? Should I avoid hills? All these questions about the force in which I was striking the ground were swirling through my head, as I continued to train, and deal with a large injury. My question was, with what force was my foot striking the ground, and what kind of terrain would injure me further? Therefore, my investigation sought out to use physics to answer this question:
What effect does inclination and pace have on the force exerted by a distance runner’s foot?
This investigation could help me in the future, as well as other runners, dealing with the real life situation of an injury, where science could answer a lot or the unknowns. In today’s sports, science is being used more and more, to investigate ways to better performance, and heal athletes correctly. This investigation could be the start to a new, high technology investigation in the professional sports world.
Newton’s Second Law of Motion Back to the top
To perform my investigation, I will use Newton’s Second Law of Motion, which states, the acceleration of an object as produced by a net force is directly proportional to the magnitude of the net force, in the same direction as the net force, and inversely proportional to the mass of the object (Newton’s Second Law). This verbal statement can be translated into the equation:
a=Fnet/m
a : acceleration (m/s/s)
F : force (Newtons)
m : mass (kilograms)
The equation above is rearranged to a more common order:
Fnet=ma
To better understand what calculating the force will mean, the unit Newtons is explained as follows:
1 Newton = 1 kg • m/s2
One Newton is defined as the amount of force required to give a 1 kilogram mass an acceleration of 1 m/s/s (Newtons: Units and Explanation).
Newton’s Second Law of Motion in this investigation
In this investigation, I will use Newton’s Second Law of Motion to calculate the force in Newtons that my foot was exerting. The larger the force (Newtons) exerted by my foot, the larger impact I am striking the ground with, and a larger impact can be almost directly tied to a stress fracture. I will use my mass in kilograms, and obtain the acceleration by using a low g accelerometer strapped to my ankle. I will be looking for the smallest force, and what terrain that happens on, and whether it happens when I run slower or faster.
Experimental Design Back to the top
The purpose of this investigation is to see how pace and inclination affect the force exerted by a runner’s foot. The set-up for this investigation included a runner on a treadmill, a Logger Pro ® accelerometer, and force calculations (Logger Pro®." Logger Pro® Vernier Software & Technology).
Variables
The independent variables are the changes I made to the pace and inclination of the treadmill I’m running on. The dependent variable is the force exerted by my foot, in Newtons, which those changes cause. The control variables included the same treadmill being used, the same accelerometer, the same computer, and I was the one to perform all of the running tests. The data was all gathered on the same day, and it was done indoors, meaning weather was not a factor.
The Runner
I began my experiment by having a teammate do the actual running. However, after a few trials, I decided that I wanted to be the one to do the running, in attempt to also add in the knowledge of how each running variation felt. For example, did it feel like I was striking the ground harder when I was running faster? I stopped the experiment, and restarted with me doing the running portion.
A treadmill was used, which enabled me to change the pace and hold it consistently, as well as choose an exact incline percentage to run at, which then physically raised the treadmill to that degree and held it there until stopped. It allowed for an accelerometer to be strapped to my ankle, which is how I gathered data as I ran. A safety tab was also within reach to stop the treadmill if needed.
As I ran for 60 seconds at each of these changes, the accelerometer read my acceleration throughout that whole minute. After each pace and incline, the graph was saved, reset, and the next trial began. This series of five paces and six inclines was done 3 times each.

The two tests were:
1) Five different paces on an all flat surface
2) Same pace on six altering inclines
The alterations to pace and incline were as follows, and each was run for 60 seconds:
|
Flat Surface |
Incline all at 8 minute pace |
|
8:00 minute pace |
0% |
|
7:30 |
3% |
|
7:00 |
6% |
|
6:30 |
9% |
|
6:00 |
12% |
|
|
15% |
*For the inclination test, the data from 8:00 minute pace on a flat surface was used also as the data for 0% incline at 8 minute pace
Acceleration
An accelerometer from Logger Pro ® , Vernier Software and Technology was used to gather the accelerations of my foot. It was a low g accelerometer that measured acceleration in m/s/s. I situated the accelerometer on my ankle, at the correct angle so that when there was no movement, it read approximately -9.81 m/s/s: gravity.

The Logger Pro ® , Vernier Software and Technology accelerometer was connected to a computer interface, where application displayed the acceleration gathered in a line graph. I then took the acceleration for each pace and incline, and found the average of the three trials, to get one value for acceleration for each variable.
Here is an example of what the acceleration graphs would show for each trial:
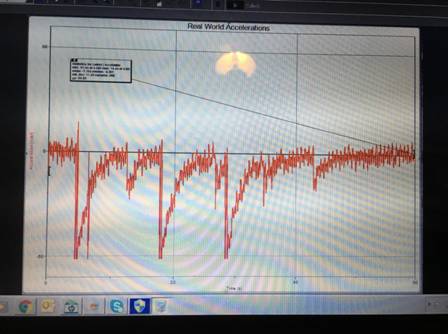
The data is both positive and negative because I am striking downward, but with each step, the foot also lifts up for a slight second before going back down.
Mass
My mass was 109 pounds, which I calculated to be about 49.4416 kilograms.
1 (kg) / 2.2046226218 (lbs) = 0.45359237 (kg/lbs)
0.45359237 (kg/lbs) / 109 (lbs) = 49.44156833 (kg)
Design Reasoning
This design enabled me to observe the data while conducting the experiment in a somewhat controlled environment. The treadmill was a great way to maintain a steady pace and inclination. I would have liked to conduct the experiment on a downhill as well, but the technology available to me would not allow it due to the necessity for a computer to be connected to the accelerometer as I ran.
The validity of the accelerometer that I had access to can be questioned. It was an old piece of equipment, with some makeshift fixes added to it. The low g accelerometer could have also accounted for some of the error in my data, as it might not have been the greatest fit for a couple of my variables, but it was the only equipment available.
Hypothesis Back to the top
I believe that a larger incline will decrease the force exerted by the runner’s stride, and running on level ground at a quicker pace will also decrease the force exerted.
Gathering Data Back to the top
For each variation, the Logger Pro ® , Vernier Software and Technology accelerometer created an acceleration graph, which I then saved. I found the average acceleration that happened over the entire minute of running, which left me with three average accelerations for each pace or inclination variation. I then took the average of those three accelerations, which left me with one average acceleration for each pace and inclination percentage.
I then took those accelerations, along with my mass, to use Newton’s Second Law of Motion to calculate the force in Newtons. I applied F=ma to each acceleration, and came up with the following data tables:
Ex: F=ma
F= (49.4416 kg)(-1.751 m/s/s)
F= -85.5722 N
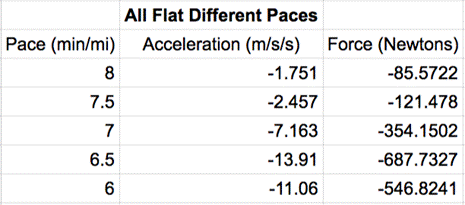
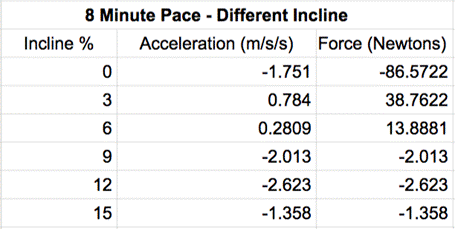
Before taking the averages again, I took the absolute values of the accelerations and forces, which allowed for an easier graph to evaluate. The negative only meant that the acceleration was down, therefore creating a downward force, but for the purpose of this investigation, the direction of the fore did not matter, simply the magnitude of it is what we are looking at.
AVERAGE - Different Pace on Flat Surface
|
Pace (minutes per mile) |
Force (Newtons) |
|
8 |
85.5722 |
|
7.5 |
121.478 |
|
7 |
354.1502 |
|
6.5 |
687.7327 |
|
6 |
546.8241 |
AVERAGE - Same Pace - Different Incline Percentage
|
Incline Percentage (all at 8 min pace) |
Force (Newtons) |
|
0% |
86.5722 |
|
3% |
38.7622 |
|
6% |
13.8881 |
|
9% |
99.5259 |
|
12% |
129.6853 |
|
15% |
67.1417 |
Graphs and Evaluation Back to the top
That data was then turned into bar graphs, to evaluate the magnitude of the forces, dependent on the pace in which I ran, and the incline in with I ran at 8 minute pace. The graphs were as follows:
Different Paces on a Flat Surface
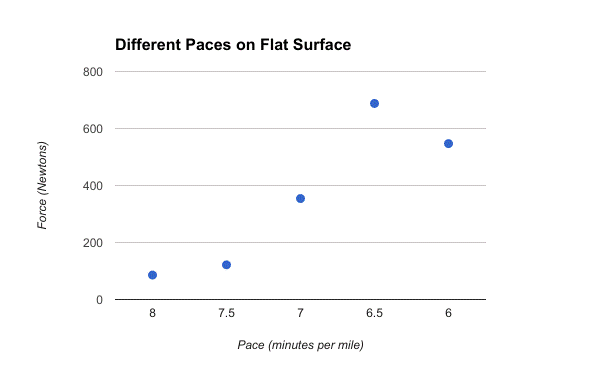
The data for this experiment proved the opposite of my hypothesis. I guessed that a faster speed would create less force, but the data shows that as the pace became faster, the force became greater as seen when the speed was 8 minutes per mile, the force was about 85.57 Newtons and when the pace was 6.5 minutes per mile, the force was about 687.73 N. This held true however, only through 6.5 minute pace. 6 minute pace was not too far off, but it did not exactly follow the trend, showing a force of about 546.8 N. This could be for a couple reasons. First of all, as a competitive cross country runner, I race 5 kilometer races, and my race pace is right about 6 minute pace. That is the pace that I use at practice, and also race in, therefore, I may have subconsciously adapted my form at that pace, since I use it for racing. Racing is about being efficient, and striking the ground with a smaller force has more efficiency, so I may have developed that habit, which shows in the data for 6 minute pace. Another reason for the inconsistency could be the validity of the low g accelerometer. This may have been too quick of a pace for it to pick up accurate data at that pace. My physical limitations however did not allow for me to test much past 6 minute pace, especially with fatigue happening after multiple trials, which would have allowed me to see if the 6 minute pace test was just inaccurate, or if it actually is an outlier.
In conclusion, running slower will result in a smaller force exerted by a runner’s foot on the ground. This makes sense because runner faster should increase acceleration, and mathematically, the faster the acceleration, the larger the force, when using F=ma.
Same Pace - Different Incline Percentage
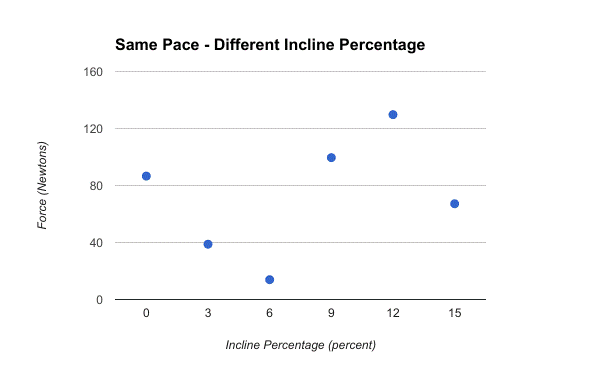
This data set showed little correlation, and therefore did not prove my hypothesis either correct or incorrect. A 9 percent incline and 12 percent incline showed to have the most force with about 99.5 N and 129.7 N, but I had predicted the opposite. I predicted that a larger incline will create a smaller force, because as qualitative data, I feel like I strike the ground softer when going up a hill, because speed slows down and my foot stays closer to the ground. However, since I ran all of the inclines at the same speed, that could have lead to the lack of conclusion. But after seeing the data, my hypothesis isn’t disproven or proven. It would also make sense for the force to be greater on a large incline, because to propel yourself up the next step, you would need to exert a larger force. Running uphill also greatly changes your running form, which would cause the runner to have a smaller stride. This means that in the one minute that I ran, my foot hit the ground many more times than in the other tests. This would alter the data because of the proportion of strikes and time the foot spend accelerating along with the same amount of distance traveled.
This inconclusive data and lack of correlation could either mean that there really is no connection between force and inclination levels, or that the data simply didn’t represent what really happens. From personal experience, I believe that uphill would have an effect on the force in which your foot strikes the ground. Because the accelerometer was attached to my ankle, it could have possible caused it to collect data at an angle that would change the data.
Conclusion Back to the top
Revisit Hypothesis
Overall, my data did not support my hypothesis. The faster I ran, the larger the force I exerted, and as for inclination, there was no evident correlation to force.
The data about pace makes sense because running faster would create a faster acceleration, and mathematically, a larger number for acceleration would equal a larger force. The conclusion for inclination could have been a methodological error, or it could really have no correlation.
My racing pace could have affected my data, as well as the way I strike my foot. Runners can either have a toe strike, mid strike, or heel strike form. They mean what they sound like, and often, depending on speed, your strike will change. When running uphill, you tend to have more of a toe strike, and for me personally, when I run fast, I lean more towards a mid strike. This could greatly impact the data because a heel strike is probably the hardest impact, from what I have felt, but it can vary depending on the person.
Cadence is also something that can greatly affect the force exerted by my foot, and is something that I would have liked to investigate if I had the correct tools available. Perhaps having a higher cadence would decrease the force exerted per step because it is increasing steps to travel the same distance and spread out the force.
To answer the stress fracture issue, those who are trying to exert the smallest force possible on their foot should try to run slow. I am not conclusive on the answer for hills, but my data proved, fairly well, that running slower will decrease the force exerted.
Possible methodology errors
The method of my experiment was
satisfactory, given the equipment at my disposal. However, the accelerometer
could have created a large error. It was strapped to my ankle, which was
accurate with reading my acceleration, but it was not strictly vertical and
horizontal acceleration. 
A foot makes all kinds of non lateral movement as well, which was impossible to account for in my data, considering the equipment I had.
Running outside would have been more accurate for actual runners, as we spend our time running on surfaces like sidewalks and roads, but in order to gather data, a treadmill had to be used. It turned out to be a very good method because of its consistency in holding my pace and exact incline.
One large methodology error that could have contributed was that I was the only one performing the experiment, so therefore I was running quite a bit. I ran a total of 11 miles to perform this experiment, and as I became more exhausted from the quick pace and high inclination, my form could have changed, therefore having an effect on my data.
Limitations
My access to equipment was limited, resulting in possible data errors. My accelerometer was low g and was very old, which could have had some high inaccuracy during my experiment. Testing more speeds would have also been ideal, but considering that I am human, I cannot go past a certain pace and be able to hold it. I would have liked to test different paces on an incline for example, but I could not run much faster than 8 minute pace on the 15 percent incline for 60 seconds.
I also would have liked to test downhill, because from experience I can predict that a steeper downhill would increase force. Mathematically this makes sense as well, because down hill makes you run faster, and therefore means larger force. Being on a treadmill however, it does not have a downhill setting, and because of my accelerometer, I had to be attached to a computer at all times, leaving me unable to test this on a real downhill. The treadmill was however a strength in the experiment as well, because it allowed me to consistently hold the same pace and also hold the same inclination by the hit of a button.
Improvements
To improve my experiment, I would purchase a better and newer accelerometer. Perhaps there is one that could work with bluetooth, and be able to separate vertical and horizontal acceleration (Sauser).
More trials can also always better your experiment, so if I could have taken breaks and rested to do more trials, I might have had more accuracy. Testing different runners would also probably improve my investigation, and allow me to evaluate the runner’s form effect on force as well. Testing downhill would be a great aspect to add, and would help answer the question for runners, about which terrain to avoid or stick to if you’re dealing with a stress fracture. Testing different surfaces as well would give great results. I’m sure striking the ground on grass for gravel has a different effect than cement or a treadmill platform.
Overall, better technology would allow for a lot more freedom in my experiment, and it would allow me to test many different variables that can affect force. I hope that this technology will exist someday, and it will be able to help athletes personalize training to be the most efficient, and the most safe for their own personal needs.
http://www.physicsclassroom.com/class/newtlaws/Lesson-3/Newton-s-Second-Law here is basic information about Newton’s Second Law of Motion
http://www.vernier.com/products/sensors/accelerometers/
here is where I got my Vernier Accelerometer
http://hypertextbook.com/facts/1999/SaraBirnbaum.shtml some other similar studies done at University of Oregon
https://runnersconnect.net/runners-guide-to-stress-fractures/ information on stress fractures
https://medium.com/starts-with-a-bang/throwback-thursday-the-physics-of-an-inclined-treadmill-2dd2dfe1594d walking and running uphill – physics mechanics
Bibliography Back to the top
"Accessibility Links." Foot Clearance | LMAM. N.p., 07 Dec. 2015. Web. 06 Feb. 2017.
"Logger Pro®." Logger Pro® Vernier Software & Technology. N.p., n.d. Web. 06 Feb. 2017.
"Newton's Second Law." Newton's Second Law. N.p., n.d. Web. 06 Feb. 2017.
"Newtons: Units and Explanation." Study.com. N.p., n.d. Web. 06 Feb. 2017.
Sauser, Brittany. "Improving Athletic Performance." MIT Technology Review. MIT Technology
Review, 22 Oct. 2012. Web. 06 Feb. 2017.