IB Physics Internal Assessment:
“What is the relationship between the temperature of a spring and its spring constant?”
Camryn Gray
Background ∙ Statement of Problem ∙ Hypothesis ∙ Method ∙ Diagram of Setup ∙ Reasoning Behind Design ∙ Raw Data Table ∙ Calculations ∙ Calculated Data Table ∙ Discussion of Uncertainty ∙ Data Table with Uncertainty ∙ Graph ∙ Conclusion ∙ Related Sites ∙ Bibliography ∙ Return to Research
Background Back to Top
Springs are used in the construction of many objects that are around us every day: pens, cars, clocks, the list goes on and on. Springs are actually fairly complex and intertwined with numerous physics applications, despite their simple exterior (Schwarz). A spring can be elongated or compressed by applying a force, but when that force is removed, the spring returns to its original shape. Because of this unique property, a spring is considered to be elastic. Springs exert a restoring force after they have been stretched or compressed which help return them to their original length (Woodford). Hooke’s law shows that the restoring force is proportional to the distance the spring has been compressed or elongated.
F = kx
In this equation, F represents the restoring force, x is the distance the spring has been stretched or compressed, and k is the spring constant (Giancoli). Each spring has a unique spring constant; the greater the value of k, the stiffer the spring will be. The variable F can be measured with a force meter and can be manipulated by pulling or compressing the spring more. It’s measured in Newtons. The distance variable, x, is measured in metres, which a ruler. The spring constant, k, is found by using Hooke’s law and has the units of N/m (Schwarz).
In physics, when heat is applied to an object that object tends to expand; its volume is increased ("Expansion"). Conversely, when the temperature of an object is decreased that object will tend to contract; its volume is decreased. The reason objects expand or contract based on the heat applied to them is because of the change in energy. When heat is applied the atoms in the object have a greater kinetic energy and they bounce off one another making the average atom separation larger; which makes the object larger as well (Allain).
Statement of Problem Back to Top
The purpose of this investigation is to answer the research question: what is the relationship between the temperature of a spring and its spring constant?
Hypothesis Back to Top
I believe that the spring constant is going to decrease slightly when the temperature of the spring is increased. This will occur because the spring will expand slightly with the increased heat, causing it to be less stiff.
The temperature of the spring will be measured indirectly, by measuring the temperature of the water bath the spring is placed in. The spring constant is defined as the force required to compress or elongate the spring divided by the distance the spring was stretched or compressed. Some of the controlled variables are the length of the spring, the distance the spring is pulled, the material of the spring, and the temperature of the water baths.
Method Back to Top
To set up my experiment I used a variety of lab equipment: a hot plate, a 1000 mL beaker, a ring stand, a test tube clamp, 900 mL of water, a ruler, a force scale, a thermometer, a piece of metal to hold the spring, and a plastic spring. The piece of metal used to hold the spring was about a foot long and had a screw with a small eyelet screwed into it.
For my setup, I filled the beaker with 900 mL of water and placed that on the hot plate. I attached the test tube clamp to the ring stand; this was placed next to the hot plate. The piece of metal used to hold the spring was secured with the test tube clamp so that it was submerged in the water. I looped the spring through the small eyelet in the metal so that it was also submerged in the water.
To gather my first data point, I measured the room temperature of the water and recorded this. I then held the ruler in the water so the bottom lined up with the bottom of the spring. After that, I hooked the force scale to the top of the spring and pulled it up so the top of the spring was at the 15 cm mark on the ruler, this displaced the spring 10.5 centimeters from equilibrium. As I was holding the spring in its stretched position, I made note of the number on the force scale and recorded this.
After getting my first data point, I turned the hot plate on to start heating up the water and the spring. I continued to measure the temperature of the water and took a new data point each time the temperature rose by five degrees Celsius. I gathered my data the same way I did for the first data point, allowing the spring to heat up in the water in between each new data point.
Diagram of Experimental Setup Back to Top
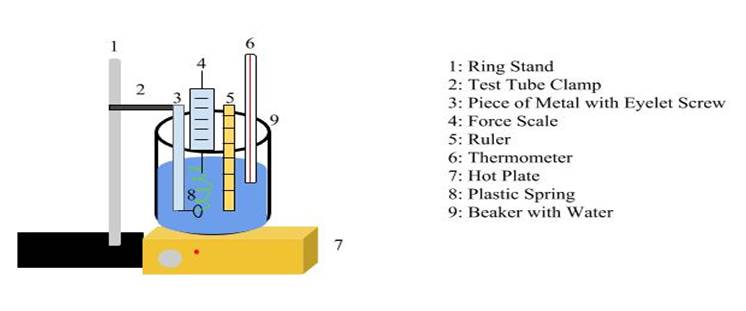
Reasoning Behind Experimental Design Back to Top
To test the effect of the temperature and its spring constant I needed a way to manipulate the temperature of a spring. I decided the easiest way to do this was so submerge the spring in water of varying temperatures. I would heat the water with a hot plate, and the spring would be heated by the water surrounding it. Because of this, I needed an experimental setup that contained water in a large enough amount that could cover the spring; this is why the beaker is 1000 mL.
The other important element of my design was a way to hold the spring under the water in a way that would allow it to be stretched upwards. This is how the metal with the eyelet screw came about. While not entirely streamlined, the contraption helped me collect the data I required. The data in the following table was collected in one trial.
Data Table with Raw Data Back to Top
|
Temperature in oC (± 0.5 oC) |
Force in N (± 0.05 N) |
|
21 |
1.6 |
|
26 |
2.0 |
|
31 |
1.7 |
|
36 |
2.1 |
|
41 |
1.7 |
|
46 |
1.5 |
|
51 |
1.7 |
|
56 |
1.5 |
|
61 |
1.6 |
|
66 |
1.4 |
Calculating the Force Constant Back to Top
The force constant can be calculated using Hooke’s Law. The three variables used in this equation represent force, the distance the spring was pulled, and the spring constant. For each temperature variation, the spring was stretched 10.5 cm away from equilibrium. An example of calculating the force constant is shown below.
1.6 N = 0.105 m (k)
k = 15.2 N/m
For each data point I followed this procedure to calculate the force constant for each temperature variation.
Data Table with Calculated Values Back to Top
|
Temperature in oC (± 0.5 oC) |
Spring Constant in N/m |
|
21 |
15.2 |
|
26 |
19.0 |
|
31 |
16.2 |
|
36 |
20.0 |
|
41 |
16.2 |
|
46 |
14.3 |
|
51 |
16.2 |
|
56 |
14.3 |
|
61 |
15.2 |
|
66 |
13.3 |
Discussion of Experimental Uncertainty Back to Top
When using different tools to measure data points, there will always be some extent of uncertainty. For my experiment, I took the smallest scale on each tool and divided this by 2 to find the uncertainty. Using this, I discovered that the uncertainty for the measured force was plus or minus 0.05 Newtons. The uncertainty for the distance pulled was plus or minus 0.05 cm or 0.005 m. While those are the two uncertainties that are important for finding the final uncertainty for the calculated spring constant, I also found that the amount of water was correct plus or minus 25 mL and the temperature of the water was correct plus or minus 0.5 degrees.
Since the spring constant is a quotient of two calculated values, its uncertainty is the sum of the fractional uncertainty of the operands, the two numbers divided by each other. An example of calculating one spring constant’s uncertainty is shown below.
![]() =
= ![]() +
+ ![]()
![]()
This method was used to calculate the uncertainty for each data point. This information is displayed in the following data table.
Data Table with Calculated Uncertainty Back to Top
|
Spring Constant in N/m |
Uncertainty in N/m |
|
15.2 |
±1.2 |
|
19.0 |
±1.4 |
|
16.2 |
±1.2 |
|
20.0 |
±1.4 |
|
16.2 |
±1.2 |
|
14.3 |
±1.2 |
|
16.2 |
±1.2 |
|
14.3 |
±1.2 |
|
15.2 |
±1.2 |
|
13.3 |
±1.1 |
Graph Depicting Calculated Values and Uncertainty Back to Top
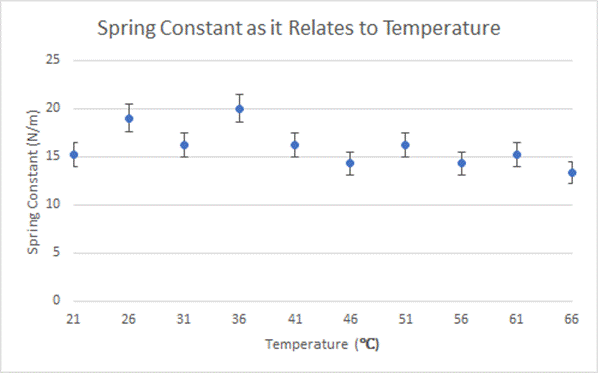
Conclusion Back to Top
After analyzing my data it can be seen that there is no distinct pattern between the temperature of the spring and the spring constant. This does not support my hypothesis, in which I predicted the spring constant would decrease as the temperature of the water increased. While my data did not directly support my hypothesis, this could be for a variety of reasons. The uncertainty for each spring constant is extremely high, showing that the data may not be completely accurate. If the experiment was done again with more precise tools, perhaps my original hypothesis may have been more accurate.
Another potential hypothesis is that the spring constant of a heavy duty spring changes proportionally with the temperature of the spring. The quality of my springs was incredibly low. In fact, one of my springs melted just as it reached 68 degrees. This shows me that the cheap plastic which comprised my springs wasn’t super sturdy. It may have been that the low quality of my springs led the erratic data that seemed not to show a constant pattern.
Further research surrounding the connection between springs and temperature could test how temperature affects springs with the same constant to start but are made of different materials. This would illustrate how different materials are affected by temperature in different ways.
Since my data did not show any correlation between the spring constant and the spring’s temperature, I wonder if the spring constant actually does remain constant. Perhaps heating the springs more directly, instead of through a water bath, may have illustrated this more clearly. It would also be interesting to not only test warm water, but also cold water. This could potentially show more variation in the spring constant due to the larger variation in temperature.
While my data did not support my hypothesis, it did show that a spring’s constant stays fairly constant!
Related Sites Back to Top
http://www.physicsclassroom.com/class/waves/Lesson-0/Motion-of-a-Mass-on-a-Spring - This site talks about the basics of springs and Hooke’s Law.
http://physics.info/temperature/ - This site discusses the basics of temperature.
http://www.4physics.com/phy_demo/HookesLaw/HookesLawLab.html - A site with more detailed information about Hooke’s Law.
http://coilingtech.com/springs-impact-everyday-life/ - Interesting information about how we uses springs in our everyday lives.
https://www.creativemechanisms.com/blog/four-different-types-of-springs - Different types of springs.
https://www.amazon.com/dp/B000CMKHDG - Really fun cat toy springs used for the experiment and later given to pet cats.
Bibliography Back to Top
Allain, Rhett. "Why Do Solids Expand When Heated?" Wired. Conde Nast Digital, 19
Aug. 2013. Web. 18 Nov. 2016.
"Expansion." Columbia Electronic Encyclopedia, 6Th Edition (2016): 1. MAS Ultra -
School Edition. Web. 18 Nov. 2016.
Giancoli, Douglas C. Physics: Principles with Applications. Upper Saddle River, NJ:
Pearson/Prentice Hall, 2009. Print.
Schwarz, Casey M. "Springs." Physics: Forces & Energy (2014): 1. Science
Reference Center. Web. 18 Nov. 2016.
Woodford, Chris. "How Do Springs Work? | How Do Springs Store Energy?" Explain
That Stuff. Explainthatstuff!, 01 July 2016. Web. 18 Nov. 2016.