Potential Energy: The Study of a Bouncing Tennis Ball
IB Physics Internal Assessment
Written By: Riley Steele
Table of Contents: Go Up
Tennis balls were originally invented for the sport of tennis, but they make a great test subject for physics experiments. Masses of tennis balls range between 56.0 and 59.4 grams (2011). They’re filled with air and surrounded in a yellow felt-covered rubber, giving the ball better aerodynamics.
Energy can be stored in an object by lifting the object to a certain height. This energy is called gravitational potential energy. The potential energy of an object depends on how heavy the object is and how high it is. The heavier an object is, the more potential energy it has, and the higher an object is, the more potential energy it has (Phun Physics). Potential energy is the energy acquired as work is being done to an object and kinetic energy is the energy released by the object as it is doing work (2003). As the ball hits the floor and bounces up, it is gaining potential energy on the way to its maximum height. The higher from the ground that the ball is dropped, the higher the ball will bounce. This elastic potential energy is why the ball is able to bounce, or rebound (msichicago.org). Therefore, as the ball loses potential energy, it won’t be able to bounce as high.
A ball is able to bounce because the force of the ball hitting the ground puts an equal force back on the ball. When the ball is about to make contact with the ground, its kinetic energy is at a maximum. As soon as the ball hits, it becomes deformed, and its potential energy is at its maximum. The ball then rebounds and reshapes itself, while its stored energy reappears (Bloomfield). Therefore, it is expected that a tennis ball has a limited ability to store energy due to the constant morphing of its shape.
Experience tells us that the ball can never bounce back to its original height (2003). The falling ball loses some of its energy to air friction, to internal forces within the ball, and to friction between the ball and the ground on impact. After the first bounce, energy is typically lost because of air resistance. The next couple of bounces lose energy as the ball changes shape and becomes warmer (GCSE). The final bounces lose energy to air resistance again.
The potential energy of an object can be defined as PE=mgh, incorporating the mass of the object, gravity, and the height (Giancoli).
The purpose of this investigation is to determine the relationship between the percentage of potential energy lost in the rebound of a tennis ball versus the height it is dropped from.
If the tennis ball is dropped from a larger height, the percentage of potential energy lost will be greater because the ball will fall a for a longer amount of time, which means it will lose more energy through air friction and from the larger impact of the ground. Height is defined as the distance between the ground and the spot the ball is dropped from. Percentage of potential energy lost is measured by the bounce height after the drop. Controlled variables include, but are not limited to, the mass of the tennis ball and gravity.
In order to collect all the data for this experiment, I will first gather all materials necessary. Then, I will tape three meter sticks to the wall, stacked on top of one another, and place the ladder as close to it as possible. My phone will be set up on a tripod across the room in order to record videos of the tennis ball dropping.
Each video consists of me precisely dropping the tennis ball from 10 different heights and watching it bounce to completion. Once I record 30 different videos, 3 trials of 10 variations, I will upload them into LoggerPro and do video analysis to discover the height of the 1st bounce of every single drop.
This experiment included the use of a tennis ball, meter sticks, tape, a tripod, a phone as a video camera, and a ladder.
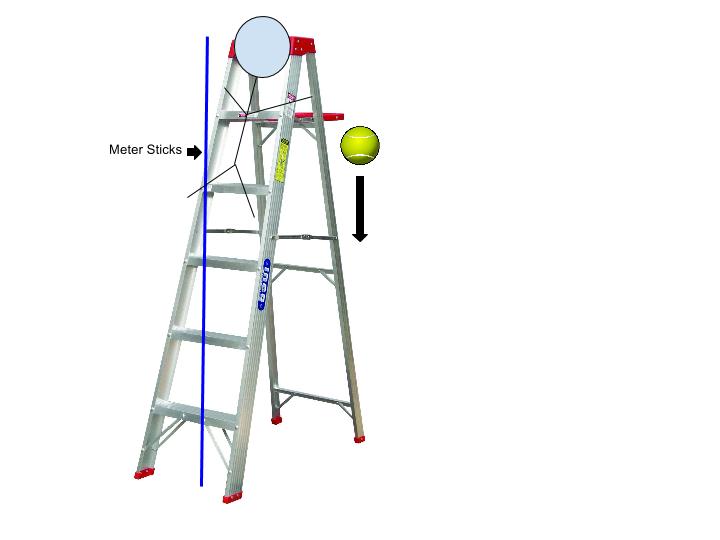
*not drawn to scale
|
Drop Height |
Bounce Height: Trial 1 |
Bounce Height: Trial 2 |
Bounce Height: Trial 3 |
Bounce Height: Average |
|
0.3 m |
0.2063 |
0.1954 |
0.2062 |
0.2026 |
|
0.6 m |
0.3588 |
0.3906 |
0.3913 |
0.3802 |
|
0.9 m |
0.5509 |
0.5480 |
0.5585 |
0.5525 |
|
1.2 m |
0.7240 |
0.7216 |
0.7160 |
0.7205 |
|
1.5 m |
0.9211 |
0.9261 |
0.9224 |
0.9232 |
|
1.8 m |
1.0562 |
1.0474 |
1.0884 |
1.0640 |
|
2.1 m |
1.2086 |
1.2240 |
1.2182 |
1.2169 |
|
2.4 m |
1.3145 |
1.3438 |
1.3629 |
1.3404 |
|
2.7 m |
1.4805 |
1.4779 |
1.4710 |
1.4765 |
|
3.0 m |
1.6222 |
1.6389 |
1.6661 |
1.6424 |
After analyzing all 30 videos in LoggerPro, I was able to find the height of the first bounce of the tennis ball. All of these heights can be seen in the table above. I found the uncertainty of the bounce height to be about 1 centimeter. The uncertainty of the average bounce height is the range of the bounce heights (high-low) divided by 2. Then, I averaged all of the bounce heights, to find the average bounce height that is needed to find the percentage of potential energy lost. These calculations can be found in the table below.
|
Drop Height |
Average Bounce Height |
Percentage of PE Lost |
|
0.3 m |
0.2026 |
(1- |
|
0.6 m |
0.3802 |
(1- |
|
0.9 m |
0.5525 |
(1- |
|
1.2 m |
0.7205 |
(1- |
|
1.5 m |
0.9232 |
(1- |
|
1.8 m |
1.0640 |
(1- |
|
2.1 m |
1.2169 |
(1- |
|
2.4 m |
1.3404 |
(1- |
|
2.7 m |
1.4765 |
(1- |
|
3.0 m |
1.6424 |
(1- |
In order to calculate potential energy, the formula PE=mgh is used, where m is mass in grams, g is gravity, and h is height in meters. In this experiment, the mass of the tennis ball and gravity stayed the same, so I only needed to use the drop height and bounce height. The bounce height was divided by the drop height to find the ratio, and then that was subtracted by 1, since it was percent lost. Using the percentages of potential energy lost that I discovered, I was able to graph my data, which can be seen below. Once the points were plotted, it became apparent that the line of best fit for this function would be exponential, which means at a certain point, a very large drop height won’t lose much more potential energy than a height slightly smaller than it.
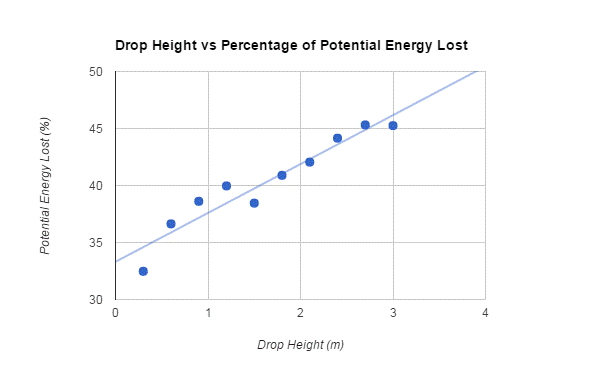
Through this experiment, I was able to prove my hypothesis to be true. As the height that a tennis ball is dropped from increases, the percentage of potential energy lost also increases. This is due to the increase of time in the air as the drop height increases. There’s a lot more air friction on the ball when it is dropped from a larger height, so it will lose more energy and won’t be able to bounce as high. Also, when the ball hits the ground, it creates friction, which decreases its energy. Therefore, if a ball is dropped from a larger height, its velocity will be much higher upon impact, which creates more friction and decreases the ball’s energy even more. Additionally, when the ball hits the ground, it compresses and becomes morphed. This leads to the conclusion that the higher the drop, the more morphed the ball becomes, which makes it unable to bounce as high as before. Essentially, a larger percentage of potential energy is lost in the tennis ball when the drop height gets higher.
Further research could include the percentage of potential energy lost in each individual bounce of the tennis ball. This would make the study a lot more in depth and make it possible to discover the overall potential energy lost after the ball bounces to completion. I could also figure out how much more potential energy is lost in the first bounce compared to the second bounce, for example. I would expect the largest percent of energy lost to be in the first bounce, but I could extend my research in order to confirm such a hypothesis. Also, it would be interesting to see if the percentages of potential energy lost would stay the same if I were to use a different ball when conducting the experiment.
Throughout this experiment, there were clearly sources of error. As seen on the graph, there are a couple data points that are outliers. This could be due to error in the measurement of drop height. Also, when determining the height of the bounce, I had to personally click the tennis ball when doing video analysis, which may not have been completely accurate. Both of these errors could cause the heights to be off by a couple centimeters, leading to an altered percentage of potential energy lost. The data is slightly limited because I was unable to drop the ball from anything higher than 3 meters due to the unavailability of a taller ladder and higher ceilings. That definitely would’ve given be a better understanding of the relationship between drop height and percentage of potential energy lost.
http://galileo.phys.virginia.edu/education/outreach/8thgradesol/EnergyBall.htm Energy of bouncing ball lab with similar set-up
http://www.gcsescience.com/pen30-energy-ball-bounce.htm Explains potential energy to kinetic energy transfer
http://www.physicscentral.com/experiment/askaphysicist/physics-answer.cfm?uid=20080509041559 Explains why a ball has a lower bounce each time it touches the ground
http://phun.physics.virginia.edu/topics/energy.html Everything you need to know about energy
https://www.usta.com/2011_tennis_ball_specifications Information about mass of a tennis ball
"The Energy of a Bouncing Ball." University of Virginia Physics Department. N.p., 2003. Web. <http://galileo.phys.virginia.edu/education/outreach/8thgradesol/EnergyBall.htm>.
"ENERGY." Phun Physics. University of Virginia, n.d. Web. <http://phun.physics.virginia.edu/topics/energy.html>
"Energy Transfer- Bouncing Ball." GCSE Science. N.p., n.d. Web. <http://www.gcsescience.com/pen30-energy-ball-bounce.htm>.
"2011 Tennis Ball Specifications." USTA. N.p., 2011. Web. <https://www.usta.com/2011_tennis_ball_specifications/>.
Giancoli, Douglas C. "Potential Energy." Physics. 6th ed. Upper Saddle River: Pearson Education, 2009. 144-47. Print.
Bloomfield, Louis A. "Ask a Physicist Answers." Physics Central. American Physical Society Sites. Web. <http://www.physicscentral.com/experiment/askaphysicist/physics-answer.cfm?uid=20080509041559>.