Nikos Jordan

Introduction .:. Question .:. Hypothesis .:. Variables .:. Procedure .:. Calculations .:. Calculation of Uncertainty .:. Data .:. Conclusion .:. Sources .:. Links .:. {up}

INTRODUCTION {up}

When objects are submerged in water, why do they look as if they are bent? This common phenomenon can be explained by the concept of refraction. One property of light that plays a key role in this scientific event is that the velocity of light can be altered based on the medium in which it goes through (BU Physics). When light passes through, say, water, the light looks bent, creating a new angle based upon an individual’s viewpoint (The Physics Classroom); this effect is dependent on where the object actually resides. Mathematically, this can be explained by Snell’s Law, a mathematical law named after the Dutch astronomer Willebrord Snellius, who derived the formula in 1621 (InnovateUs). The formula is as follows:

Ѳ₁ is the angle of incidence and Ѳ₂ is the angle of refraction; the angle of incidence is the measure of the “angle between the incident ray and the normal,” while the angle of refraction is the “angle between the refracted ray and the normal” (Infoplease). In terms of the speed of light, travelling through a more dense medium tends to slow down the speed of light; therefore, the density of the medium in which light passes through effects the index of refraction. The purpose of this experiment is to discover how an increased concentration of sugar in water effects the angle of refraction in water. I hypothesize that when the water has a higher concentration of sugar, there will be a higher angle of refraction. I am basing this prediction off of the assumptions detailed in Snell’s Law. To determine how the angle is effected, I will measure the angle of refraction in relation to the amount of sugar that is in the water. I believe my hypothesis will be correct seeing that the angle of refraction either increases or decreases based on the density of the medium light is travelling through (Wolfram).

QUESTION {up}

How does sugar effect the refractive index of a water solution; what is their relationship?

HYPOTHESIS {up}

If the molarity of sugar water is increased by a constant amount (0.03 M), then the index of refraction will display a comparable linear increase.

VARIABLES {up}

Independent: the molarity of the sugar water

Dependent: the index of refraction of the sugar water

Controls: the angle of incidence, the distance of the prism from the wall

PROCEDURE {up}

            To perform this experiment, I placed a laser perpendicular to a wall, putting a clear triangular prism in front of the laser on its base. The prism was placed so as to be parallel to the wall. First, I filled the prism with plain water, measuring the distance between where the laserbeam exited the prism and met the wall (horizontal distance) and the distance between where the laserbeam struck the wall and the floor adjacent to the wall (vertical distance). Every subsequent trial of the experiment, sugar was added to the water in 0.03 M increments (approximately 2 ¼ teaspoons of sugar), and I ended the experiment when the molarity reached 0.12 M. I retook the same type of measurements I took at the very beginning of the experiment with the plain water every trial to collect my data.

CALCULATIONS {up}

            Given the measured vertical and horizontal distances, calculating the index of refraction was complicated.

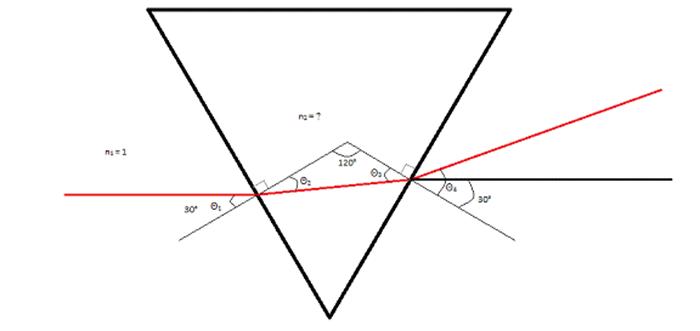
As seen in the image above, the laserbeam refracts twice. The first time the laserbeam refracts is when it first enters the prism, and the second time the laserbeam refracts is when it exits the prism. Due to this, Snell’s Law does not work, making it necessary to derive a specific equation for this situation. To do that, I utilized the different relationships between the angles in this situation. They are as follows: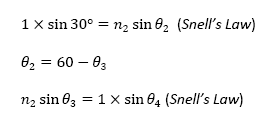

            From the above equations, I derived an equation that reveals the relationship between θ₄, the angle I could calculate given the information I had, and n₂, which is the index of refraction. The derived equation used to obtain this information is below: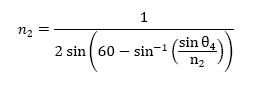

            To calculate θ₄, both the horizontal and vertical measurements that were found in each trial of the experiment were used in the following equation:

CALCULATION OF UNCERTAINTY {up}

            To calculate the uncertainty of this particular experiment, a “brute force” method was used.

DATA {up}

Molarity (M)	Horizontal (±0.05 cm)	Vertical (±0.05 cm)	Θ4 (±0.05 Degrees)	n2	Uncertainty
0.0	114.3 cm	60.96 cm	58.07	1.364	0.0029
0.03	114.3 cm	67.818 cm	60.68	1.389	0.0028
0.06	114.3 cm	73.914 cm	62.89	1.408	0.0027
0.09	114.3 cm	79.248 cm	64.73	1.423	0.0026
0.12	114.3 cm	83.058 cm	66.00	1.434	0.0025

Data File: text .:. Excel

CONCLUSION {up}

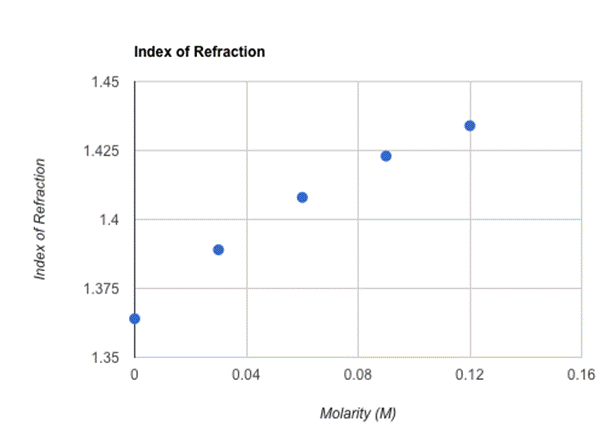
            When calculated and placed on the graph above, my results were relatively linear with an upward slope. What is highly interesting is that although Θ₄ results increased in an almost uniform manner (approximately +2 degrees with every .03 M increase), the indexes of refraction (although increasing every time in correlation with the rising molarity) lowered the extent of their increase every trial. For example, the difference between the 0.12 M index of refraction and the 0.09 M index of refraction was 0.011, while the difference between the 0.03 index of refraction and the 0.00 M index of refraction was 0.025, a slightly higher increase. Ultimately, these results indicate that my hypothesis that by incrementally increasing the molarity of sugar water in a constant amount (in this case, 0.03 M), the index of refraction will display a comparable linear increase is, indeed, correct. When substances become more dense, the angle, and thus the index of refraction, increases. In this experiment, I aimed to achieve a higher level of accuracy by widening the distance between the prism I used and the wall, which increased the measurements of the vertical and horizontal distances as well as the accuracy of the calculated angle. For each index of refraction, the uncertainties lied between 0.0025 and 0.0029, which is relatively low. Despite possessing no actual data to compare the indexes of refraction I gathered to, the index of refraction measured for 0.0 M can be compared to the largely accepted index of refraction of water which is 1.3330. I calculated 1.364 as the index of refraction for 0.0 M, offering a percent error of approximately 2.33%, which would have ideally been much lower. Some of the several sources that contributed to the error in this experiment are: an imperfect method of measuring sugar in terms of molarity, the basic difficulties of achieving entirely accurate measurements using a measuring tape, the low amounts of leaking water that plagued the entirety of the experiment, the laser not being perfectly perpendicular to the wall, and the residue in the triangular prism that likely effected the volume and sugar content of each trial. To improve this experiment and the procedures therein, a precise method of measuring sugar, a more accurate way of measuring distances, making sure the laser is perfectly perpendicular to the wall, increasing the amount of trials in the experiment, and having a cleaner prism are all ways to increase the accuracy of such an experiment.

SOURCES {up}

"The Angle of Refraction." The Angle of Refraction. N.p., n.d. Web. 29 Nov. 2015.

"Home | Boston University Physics." Home | Boston University Physics. N.p., n.d. Web. 29 Nov. 2015.

Infoplease. Infoplease, n.d. Web. 29 Nov. 2015.

"Snell's Law -- from Eric Weisstein's World of Physics." Snell's Law -- from Eric Weisstein's World of Physics. N.p., n.d. Web. 29 Nov. 2015.

"What Is Snell's Law?" What Is Snell's Law? N.p., n.d. Web. 29 Nov. 2015.

LINKS {up}

http://buphy.bu.edu/py106/notes/Refraction.html Helpful lesson on refraction and Snell’s Law with some problems to work through.

http://www.physicsclassroom.com/class/refrn/Lesson-2/The-Angle-of-Refraction Simple information on refraction.

http://www.innovateus.net/science/what-snells-law Explanation of Snell’s Law.

http://www.infoplease.com/encyclopedia/science/refraction-the-law-refraction.html Description and explanation of the law of refraction.

http://scienceworld.wolfram.com/physics/SnellsLaw.html Wolfram’s definition of Snell’s Law.